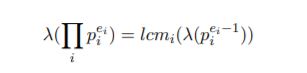IJCNC 01

Privacy Preserving Reputation Calculation in P2P Systems with Homomorphic Encryption

FUJITA Satoshi
Graduate School of Advanced Science and Engineering, Hiroshima University, Kagamiyama 1-4-1, Higashi-Hiroshima, 739-8527, Japan

Abstract

In this paper, we consider the problem of calculating the node reputation in a Peer-toPeer (P2P) system from fragments of partial knowledge concerned with the trustfulness of nodes which are subjectively given by each node (i.e., evaluator) participating in the system. We are particularly interested in the distributed processing of the calculation of reputation scores while preserving the privacy of evaluators. The basic idea of the proposed method is to extend the EigenTrust reputation management system with the notion of homomorphic cryptosystem. More specifically, it calculates the main eigenvector of a linear system which models the trustfulness of the users (nodes) in the P2P system in a distributed manner, in such a way that: 1) it blocks accesses to the trust value by the nodes to have the secret key used for the decryption, 2) it improves the efficiency of calculation by offloading a part of the task to the participating nodes, and 3) it uses different public keys during the calculation to improve the robustness against the leave of nodes. The performance of the proposed method is evaluated through numerical calculations.

Keywords

P2P reputation management, homomorphic cryptosystem, EigenTrust, Paillier cryptosystem

1. Introduction

Reputation management is a crucial task for fully distributed systems such as Peerto-Peer (P2P) systems and federated social networks since in those systems, services are provided by individual, unauthorized peers (i.e., nodes) unlike classical serverbased systems. The reputation of nodes is used not only to find high quality services as in gourmet sites, but also to identify low quality service-providers to penalize them by deliberately reducing the service quality supplied to them. Indeed, many P2P systems support reputation management as a part of the incentive mechanism, so as to encourage nodes to increase their reputation by improving the service quality supplied by those nodes.

The reputation of a node in such systems is generally calculated from trust value of nodes given by entities called evaluators (e.g., customers in the case of online shopping site). Therefore, the trust value can be an obvious target of attacks by malicious nodes who wish to Illegally raise their reputation. One way to protect such attacks is to ask trustworthy third parties to calculate trust value of the evaluatee and to keep it securely, where if trust values calculated by different entities conflict, an agreement could be achieved through majority voting. Such a consignbased approach would work well if the trust value of a node can be (automatically) generated in an objective manner, as in cases in which the contribution of an amount of upload bandwidth in parallel download systems such as BitTorrent and the forwarding of received video streams in video streaming systems such as seedess1 and P2PSP2 (if the credibility of the prepared server is questionable, we could record the history of contributions and reputation calculations as a blockchain, so that the recorded information can be verified by all nodes involved in the service).

In this paper, we consider a more general setting for the reputation management in P2P systems in which the trust value of an evaluatee is given by an evaluator in a subjective manner and the evaluator wishes to keep it secret from other nodes including the evaluatee (e.g., the reader could consider the personnel evaluation in an organization such as company and alumni meeting). To the author’s best knowledge, existing reputation management schemes for P2P systems do not take such situations into account at all and do not adequately preserve the privacy of the evaluators. In this paper, we tackle this challenging issue, and propose a method to calculate the reputation of each node in a distributed manner without disclosing any subjective trust value, with the aid of homomorphic encryption.

There are a lot of previous work concerned with the privacy preserving calculations with homomorphic encryption [11–13, 16]. Most of them assume that a trustworthy third party is commissioned to conduct the calculation on confidential data stored in a cloud server, which is encrypted with the public key of an appropriate key server. Thus, it implicitly allows the trustworthy key server to decrypt the data even if it was strictly confidential.

Such a centralized approach, however, does not work well in P2P systems for the following reasons. At first, such calculations should be realized so as to block accesses to the trust values by a node which has the secret key for the decryption. Specifically, although it could access the ciphertext of the reputation score which is the final result of calculation, it should not be allowed to access any data from which the original trust value of nodes could be inferred. Concerned with this issue, in the proposed method, we take an approach so that encrypted reputation values are successively updated through calculation to reflect the trust value of individual nodes. Although the intermediate results of the calculation are shared by all nodes, the (original) trust values cannot be guessed from them besides the fact that the sum of trust values given by an evaluator equals to a certain fixed value. The second point we need to consider is the decentralization of the reputation calculation. Existing privacy preserving schemes are designed for the bulk processing in which a central entity conducts the calculation on the data stored on a cloud server. In contrast, the data on P2P systems, including trust values, are distributed over the network from the beginning, and it is not efficient to aggregate them to a centralized server before starting the calculation. In addition, the calculation time can significantly be reduced by utilizing the computational resources of the participating nodes. In this aspect, the proposed method incorporates several techniques to improve the efficiency of the distributed processing. The third point is that due to node churn, it is not guaranteed that a node holding the secret key will stay in the system at the time of decryption. To overcome this issue, we use different public keys for the reputation calculation. The effectiveness of the proposed method is evaluated by conducting numerical calculations. The results show that the proposed method reduces the maximum circulation time used for aggregating the result of multiplications to a half, thereby reducing the time required for each round of the reputation computation, and the cost of privacy preservation is proportional to the number of nodes N, which takes about 16 seconds when N = 1024.

The remainder of this paper is organized as follows. Section 2 overviews related work. Section 3 reviews the EigenTrust reputation management system which plays a central role in the proposed method. Section 4 describes the details of the proposed method. Section 5 summarizes the results of evaluations. Finally, Section 6 concludes the paper with future work.

2. Related Work
2.1 Homomorphic Encryption

Homomorphic encryption (HE, for short) is a type of encryption which preserves the homomorphism for certain arithmetic operations3 and is classified into several types by the strength of preservations, such as partially homomorphic, somewhat homomorphic, leveled fully homomorphic, and fully homomorphic. The concept of HE was initially proposed by Rivest in 1978 [14]. Although the concrete realization of HE has been an open issue for thirty years, it was positively answered by Craig Gentry in 2009 [5] with the proposal of a fully homomorphic cryptosystem based on the lattice-based cryptography.

As a tool available to developpers who are not a specialist in cryptography, IBM released a C++ library named HElib[6]4 , which is being updated actively. The current version of HElib adopts the Brakerski-Gentry-Baikuntanathan (BGV) method and the Cheon-Kim-Kim-Song (CKKS) method, which are extentions of the Gentry’s method. The number of options available for the implementation of security systems dramatically increases if we do not stick to be fully homomorphic.

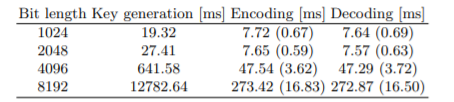
Table 1. Execution time required for the encoding/decoding in the Paillier cryptosystem. Two values in each cell show the mean and the sample standard deviation over 1000 runs, respectively.

In fact, it is widely known that RSA and ElGamal5 are multiplicative HE, and Goldwasser-Micali and Paillier [10] are additive HE, where the last one is the main player of the current paper. A typical application for additive HEs is the electronic voting, as it merely needs simple counting of votes. Other applications of additive HEs include the analysis of medical data [1] and the k-clustering of vector data [18]. A formal definition of the Paillier cryptosystem is given in Appendix to make this paper self contained, and before proceeding to the detailed explanation of the proposed method, as a preliminary experiment, we evaluated the execution time of a Python program written with the paillierlib library on a computer with Intel Core i9, 2.3 GHz, and 16 GB memory. Table 1 summarizes the results, where the key length is varied from 1024 bits to 8192 bits. From the table, we find that when the key length is 2048 bits, encoding and decoding operations can be done in 10 ms each, confirming that the Paillier cryptosystem can be used as a tool for the privacy preserving calculations.

2.2 Related Work on Reputation Management

In the literature, there are many proposals concerned with the reputation management in P2P systems. PeerTrust [15] is designed for the transaction-based feedback system and calculates the reputation of each node by considering three basic trust parameters and two adaptive factors, which include the amount of feedback received from other nodes, the number of transactions relevant to the node, the credibility of the source of feedback, and the context of transactions and the community. PowerTrust [17] takes advantage of the distribution of evaluations among nodes, which is generally not uniform but follows a power-law. Specifically, it adaptively selects a small number of nodes with the highest reputation, and leverages them to significantly improve the accuracy of calculation and the speed of convergence.

Although a detailed explanation of EigenTrust will be given in the next section, we could overview several proposals relevant to EigenTrust, as follows. Choi et al. [3] proposed Enhanced Eigentrust, which uses a beta distribution to calculate the normalized trust values. The intensive employment of trusted nodes effectively speed up the convergence in calculating reputation values. Personalized EigenTrust [2] allows each node to individually specify its trusted nodes and the method proposed in [4] recognizes such trusted nodes with the aid of Page Rank. Federated EigenTrust [7] introduces the notion of representative nodes to manage the unpredictable leave of trusted nodes. HonestPeer [9] offloads the task of reputation calculation to (honest) nodes with high ratings to legitimately increase the reputation of nodes.

3. Reputation Calculation with EigenTrust

EigenTrust provides a method to calculate the (global) reputation value of each node in a P2P system based on the (local) trust value given by each node to other nodes. Note that such a collection of trust values can be represented in the form of a square matrix. In the following, we assume that the trust value cij given by node i for j is normalized to the [0, 1] interval so that the higher the value, the higher the trust level6 . It is natural to assume that the value of cjk is trustable for i, if cij is sufficiently large (each node is assumed to have absolute trust in itself and cii = 1 holds for any i). In other words, we could assume the existence of a sort of transitivity concerned with the trust. By extending this idea, given a collection of local trust values, the reputation tik of i in k could be represented as

4. Proposed Method

There are several options to apply the notion of homomorphic cryptosystem to the reputation management in EigenTrust. One possible idea is to encrypt trust value cij and to multiply it with ei after collecting encrypted values from all nodes. However, such a naive approach does not scale since it forces the central entity to conduct all multiplications, and is less efficient than a simple centralized approach
in which all encrypted cij ’s are collected to the server before starting the calculation. Thus in the following, we will focus our attention on another approach in which the encryption is applied to reputation vector e.

4.1 Baseline

Note that since the fact of cij = 0 is hidden by applying the encryption, exactly n2 multiplications should be conducted even if the given matrix is sparse, unless the fact of cij = 0 is notified to the server through alternative route. Since the role of client i is to receive encrypted ei from the server and to return the resulting list (ei×ci1, . . . , ei×cin) to the server, if the multiplication is conducted under the Paillier cryptography, merely the results of multiplications to the trust values are collected to the server without revealing its own trust values. In addition, since an updated ei will be received from the server in the next round, two successive rounds are separated through the barrier synchronization.

4.2 Distributed Aggregation

The above C/S scheme can be extended so that the aggregation of the results is replaced by the P2P communication. More concretely, we organize the task of aggregating the result of n × n independent multiplications into several task-groups

Fig. 1. Two partitions of the set of nodes V = {1, 2, . . . , 24} with k = 4. Four subsets in U are represented by dashed blue rectangles and six subsets in V are represented by dashed red rectangles.

and to give the responsibility of controlling each task-group to a node in V in a decentralized manner. Note that such an extension of data aggregation still preserves an important nature of the baseline scheme so that each node does not have to disclose its trust values to the others.

The concrete execution of task-group Tx,y proceeds as follows. Suppose that each node i computes multiplication ei × cij by using encrypted ei received from

Fig. 2. 24 multiplications concerned with node 9 in subset U2 ∈ U. Nodes in U2 are represented by circles and multiplications conducted by node 9 are represented by simple numbers. Set of multiplications M9,y, for 1 ≤ y ≤ 6, is indicated by a dashed red rectangle which corresponds to task group T2,y since node 9 is a member of subset U2.

4.3 Adaptive Load Balancing

In the above scheme, several messages are circulated along chains in each subset Ux ∈ U to conduct the partial update of tentative reputation value of nodes in V . The final reputation vector is obtained by repeating rounds similar to EigenTrust, and the next round can start only after collecting partial updates from all subsets. Thus we could speed up the reputation calculation by reducing the maximum circulation time over all chains while keeping the number chains (recall that the C/S scheme described before trivially achieves the min-max circulation time). In the proposed method, we realize such a reduction of the maximum circulation time by using the following two techniques:

Fig. 3. Aggregation of the result of multiplications through circulating an aggregation massage. In this figure, each layer corresponds to n multiplications conducted by a node in U2, where the results for node 22 are placed at the same location in each layer. Thus, the result of partial inner product of length n/k can be obtained by aggregating the result of n/k multiplications conducted by six nodes in U2.

– Organize U so that each subset Ux in the partition consists of nodes whose mutual distance is short.
– The responsible node i ∗ monitors the circulation time of each chain managed by i ∗ , and re-organize the collection of chains so that the maximum circulation time could be minimized.

A typical realization of the first technique is to measure the round-trip time for each pair of nodes in V beforehand, and to apply the k-means method to obtain a collection of k subsets. On the other hand, the second technique can be realized by adaptively applying split and merge operations to the collection of chains in such a way that: 1) a chain with long circulation time is split into two chains and 2) two chains of small circulation time are merged into a chain. Note that if the partition U obtained by the first technique reflects the proximity of the nodes, we could assume that the transmission time to the next node on any chain derived from U is bounded by a sufficiently small value such as 50ms, and given such a subset of nodes, the second technique manages the difference of response time due to the overload of nodes.

4.4 Improve the Resilience Against Churn

In the previous description, we assumed that each element of the reputation vector is encrypted using the public key of the central key server, but this assumption can be relaxed as follows:

– Different keys can be used for each round, if it is allowed to decrypt the reputation vector after each round.

Fig. 4. The flow of reputation calculation in a round. Although only two task groups are illustrated in this figure, there are n(= k×n/k) task-groups in the system each of which aggregates the result of n multiplications. Note that the central server is used to collect the resulting reputation scores and the actual calculation is offloaded to the participants.

– Different keys can be used for each task group.
– The key used to decrypt the outcome of a task group does not have to be held by the responsible node of the task group. In fact, the task of decryption can be delegated to the responsible node of other task group. With such a refinement, the description of the overall task group is modified as follows (see Figure 4 for illustration):

1. The responsible node i∗ of a task group receives the tentative reputation value of each member from the server, and encrypts them using the public key of the node which is responsible for the decryption, or the server conducts the encryption before sending it to node i∗.
   
2. The responsible node i∗ sends the encrypted tentative reputation value to each member in the subset, conducts the partial aggregation under its control, and forwards the resulting list to the node responsible for decryption, where the resulting list contains n elements.
   
3. After receiving a list to be descrypted, the node decrypts each element in the list, and returns the result to the central server.

In the above extension, the grouping of nodes causes no load balancing effect at all but increases the total load of the nodes since each responsible node must decrypt a list of length n every round. Instead, the content of calculations in each task group is kept secret from the server and members of other subsets, which increases the level of privacy preserving compared to the C/S scheme. In addition, by delegating the task of decryption to the members of other subset, we could preserve the privacy of each member from other members in the same group including the responsible node i∗. Finally, since the role of key holders is only to decrypt the result of a task group in a certain round, it can be easily replaced by other node in each round, thereby increasing the resilience against node churn.

5. Evaluation

In this section, we evaluate the performance of the proposed method, in terms of: 1) the effect of acceleration of the data aggregation and 2) the amount of additional cost due to privacy preservation in P2P environment through numerical calculations. More specifically, as for the first point,

– We evaluate how much the circulation of aggregation message can be accelerated by using the k-means clustering and a heuristic minimization of the length of the cyclic route, by assuming that nodes are associated with a point in the three-dimensional Euclidean space, and

– We evaluate how much the maximum circulation time over all clusters can be reduced by reflecting the variance of the response time of nodes, by assuming that the response time follows a geometric distribution.

The reader should note that the node density around a node becomes sparse as the number of dimensions increases, which contradicts to the intuition such that the locality of nodes plays a crucial role in organizing efficient P2P overlay, and if the dimension is fixed to two, it becomes difficult to reflect the diversity of the locality existing in real-world networks. On the other hand, the slow-down due to privacy preservation will be estimated in Section 5.2 using the result of preliminary experiments summarized in Table 1.

5.1 Effect of Reflecting the Locality of Nodes

At first, we evaluate the effect of the k-means clustering to reduce the maximum circulation time (over all subsets) by assuming that each responsible node determines the cyclic route in a random manner. Figure 1 summarizes the results. The vertical axis indicates the ratio of the maximum circulation time obtained by the k-means method to the value obtained by applying a random partitioning (into subsets with an equal number of nodes), and the height of each bar represents the value averaged over 100 random instances generated for each combination of the number of nodes N and the number of clusters k. We confirm that no instance yields a ratio worse than 1.0, and if k ≥ 8, the k-means clustering reduces the maximum circulation

Fig. 5. Speed-up of the aggregation time by the k-means clustering compared with a random clustering into subsets of an equal size.

time of the random partitioning to almost a half, on average. Such a significant reduction should be caused by the short average distance in the resulting clusters, since the cluster size obtained by the k-means method is not necessarily equal (i.e., the maximum cluster size is larger than the random partitioning). To clarify this point, we evaluated the maximum average distance over all subsets generated by two schemes. Figure 6 summarizes the results. The average distance realized by the random partitioning gradually increases as k increases, which is because we are taking the maximum circulation time over k subsets. In the k-means method, on the other hand, since the effect of localization increases for larger k’s, the ratio to the random partitioning becomes smaller than the ratio indicated in Figure 5 (e.g., the ratio is less than 0.25 for k = 256).

Next, we evaluate the effect of circulation order to the aggregation time, which is optimized in the proposed method by using an approximation scheme based on the minimum spanning tree (MST). As the result of experiments, we confirmed that although the length of the cycle, i.e., summation of the edge weights, realized by a random ordering increases in proportion to the number of nodes in the cluster, the cycle length realized by the proposed method increased about 1.58 times when

Fig. 6. Maximum average distance over all clusters.

the cluster size doubled, on average. This value of 1.58 is roughly in line with the degree of increase in the weight of the MST for the given instance. In fact, while it is well known that the theoretical upper bound on the approximation ratio of the MST-based approximation scheme is 2.0, it was experimentally confirmed that the length of approximated solution covering randomly placed points in a 3D cube is, 1.2 to 1.3 times the weight of the MST (this ratio is slowly worsened as the number of nodes increases). In terms of the real-time, the above result roughly corresponds to the situation in which the aggregation time of 17 seconds taken by the random ordering reduces to about 4 seconds by the proposed method, when N = 512.

The effect of the load balancing reflecting the variance of the response time of nodes is evaluated as follows. In this experiment, we consider a theoretical model in which the response time of each node follows a geometric distribution with probability p. Then, we evaluated to what extent the maximum sum of the response times over all subsets can be reduced by using a greedy partitioning scheme instead of a random partitioning, by varying the number of nodes N and the probability p(note that the smaller p is, the mean and the variance of the response times become larger). The results are summarized in Figure 7. We confirm that as N increases,

Image

Fig. 7. Effect of load balancing by the greedy scheme.

the room for the improvement by the greedy scheme becomes smaller since the badness of the random partitioning will be amortized. However, even with N = 128, we can obtain a speed-up of more than 4% for any p ≤ 0.5.

5.2 Cost of Privacy Preservation

Finally, we evaluate the increase of the computation time due to the enhancement of privacy preservation. In the baseline method, encryption is conducted only once at the beginning of computation and decryption is conducted only once when the final reputation value is obtained. In the enhanced method, on the other hand, encryption and decryption are conducted for all reputation values with different keys in each round to prevent other nodes from eavesdropping the trust values. Thus, the additional overhead per round can be estimated as the time required to encrypt/decrypt one element multiplied by the number of elements. The results in Table 1 imply that when the number of elements is N, the time required for encryption and decryption is 7.65N [ms] and 7.57N [ms], respectively; e.g., when
N = 1024, it takes about 8 seconds for encryption and decryption, respectively.

Note that this cost can be mitigated by conducting the encryption/decryption once every few rounds, rather than every round.

6. Concluding Remarks

In this paper, we propose a method to extend the EigenTrust reputation management system with the notion of homomorphic cryptosystem so that the privacy of evaluations is protected from other nodes. Experimental results show that the proposed method reduces the maximum circulation time used for aggregating the result of multiplications to a half, thereby reducing the time required for each round of the reputation computation, and the cost of privacy preservation is proportional to the number of nodes N, which takes about 16 seconds when N = 1024. A future work is to implement the proposed method in existing P2P systems.

Conflicts of Interest

The author declares no conflict of interest.

References

1. A. Ara, M. Al-Rodhaan, Y. Tian, and A. Al-Dhelaan. A secure privacy-preserving data aggregation scheme based on bilinear ElGamal cryptosystem for remote health monitoring systems. IEEE Access, 5, pp. 12601–12617, 2017.
   
2. N. Chiluka, N. Andrade, D. Gkorou, and J. Pouwelse. Personalizing EigenTrust in the Face of Communities and Centrality Attack. in Proc. IEEE 26th Int’l Conf. on Advanced Information
   Networking and Applications, 2012.
   
3. D. Choi, S. Jin, Y. Lee, and Y. Park. Personalized eigentrust with the beta distribution. ETRI Journal, 32(2):348–350, 2010.
   
4. P. A. Chirita, W. Nejdl, M. T. Schlosser, and O. Scurtu. Personalized Reputation Management in P2P Networks. in Proc. ISWC Workshop on Trust, Security, and Reputation on the Semantic Web, 2004.
   
5. C. Gentry. Fully Homomorphic Encryption Using Ideal Lattices. in Proc. the 41st ACM Symposium on Theory of Computing (STOC), 2009.
   
6. S. Halevi and V. Shoup. Algorithms in HElib. In Proc. CRYPTO 2014: Advances in Cryptology, 2014, pages 554–571.
   
7. R. Jansen, T. Kaminski, F. Korsakov, A. S. Croix, and D. Selifonov. A Priori Trust Vulnerabilities in EigenTrust. Technical report, University of Minnesota, 2008.
   
8. S.D. Kamvar, M.T. Schlosser, H. Garcia-Molina. The Eigentrust algorithm for reputation management in P2P networks. in Proc. 12th Int’l Conf. on World Wide Web (WWW ’03), 2003, pages 640–651.
   
9. H. A. Kurdi. HonestPeer: An enhanced EigenTrust algorithm for reputation management in P2P systems. Journal of King Saud University – Computer and Information Sciences (2015) 27, 315–322.
   
10. P. Paillier. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. in Proc. EUROCRYPT 1999, pages 223–238.
    
11. M. M. Potey, C. A. Dhote, and D. H. Sharma. Homomorphic encryption applied to the cloud computing security. Procedia Computer Science, 79, pp. 175–181, 2016.

12. M. Tebaa, S. E.Hajji, and A. E. Ghazi. Homomorphic encryption method applied to Cloud Computing in Proc. National Days of Network Security and Systems, 2012.
    
13. M. Tebaa and S. E. Hajji. Secure cloud computing through homomorphic encryption. Computer Science, ArXiv, Corpus ID: 21074700, 2014.
    
14. R. L. Rivest, L. Adleman, and M. L. Dertouzos. On data banks and privacy homomorphisms. In Foundations of Secure Computation, 1978.
    
15. L. Xiong and L. Liu. PeerTrust: supporting reputation-based trust for node-to-node electronic
    communities. IEEE Trans. Knowledge and Data Engineering, 16(7):843–857, 2004.
    
16. F. Zhao, C. Li, and C. F. Liu. A cloud computing security solution based on fully homomorphic encryption. in Proc. 16th Int’l Conf. on Advanced Communication Technology, 2014.
    
17. R. Zhou and K. Hwang. PowerTrust: A Robust and Scalable Reputation System for Trusted Peer-to-Peer Computing. IEEE Trans. Parallel and Distributed Systems, 18(4):460–473, 2007.
    
18. Y. Zhu and X. Li. Privacy-preserving k-means clustering with local synchronization in peerto-peer networks. Peer-to-Peer Networking and Applications, 13, pp. 2272–2284 (2020).

A Paillier Cryptosystem

To make this paper self-contained, we give a formal definition of Paillier cryptosystem which plays a crucial role in the proposed method.

A.1 Euler’s Theorem

We begin with an important theorem in the number theory, which is known as the Euler’s theorem.
Euler’s Theorem For any mutually prime positive integers n and a, it holds

where ϕ(n) is the Euler’s totient function which returns the number of integers in {1, 2, . . . , n} which are mutually prime to n.

As an extension of the Euler’s totient function, Paillier cryptosystem uses a function λ(n) satisfying a λ(n) ≡ 1 (mod n) for any mutually prime integers n and a. By the Carmichael’s theorem, function λ(n) is represented as

and for odd prime p,

where the last equation is used to certify the correctness of the decryption in Paillier cryptosystem.

A.2 Encryption/Decryption

Paillier cryptosystem is a public key cryptosystem. Secret key, which is used for the decryption, is a pair of sufficiently large prime numbers (p, q), and public key (g, n), which is used for the encryption, is generated as n := p × q and g := (kn + 1) mod n 2 , where k is a random number drawn from Zn. Given a public key (g, n), the ciphertext c of a message m satisfying 0 ≤ m < n is calculated as

where r is a random number in Zn which is independently selected for every time of the encryption. On the other hand, the decryption of a given ciphertext c is conducted as:

Recall that by the Carmichael’s theorem, aλ ≡ 1 (mod n) holds for any mutually prime integers a and n, and since c and g are residuals of a division by n2 , a and n are certainly mutually prime. The decryption of c uses λ which is calculated from the secret key (p, q), but it is secured by the fact that the factorization of n is computationally hard. Now let us verify whether the above procedure certainly decrypts c to plaintext m. At first, cλ is calculated as

where the last equality is derived from (1+an) k ≡ 1+ank (mod n 2), which can be proven by using the binomial theorem. Note that the above operation eliminates the random number r used in the encryption. Similarly, gλ can be calculated as

Thus, by applying function L to them, we have

which certainly realizes the decryption.

A.3 Additive Homomorphism

Pailier cryptosystem satisfies the additive homomorphism in the sense that the decryption of the product of two ciphertexts equals to the sum of plaintexts. Let c1 and c2 be ciphertexts of messages m1 and m2, respectively, and let c := c1 × c2 mod n2 . Then, since

the additive homomorphism certainly follows. It is also known that Pailier cryptosystem satisfies a property such that decrypting the ciphertext of m1 to the power of m2 yields m1 × m2. Let c1 be the ciphertext of m1 snd c := cm21 mod n2. Then, since

this property certainly follows.