IJCNC 01

Deep Reinforcement Learning-Based Resource Allocation in Massive MIMO NOMA Systems

Pham Hoai An1, 2, Nguyen Dung1, 2, Nguyen Thi Xuan Uyen1, 2, Nguyen Thai Cong Nghia1, 2, Ngo Minh Nghia1, 2* 1 VNUHCM – University of Science, Ho Chi Minh City, Vietnam 2 Vietnam National University, Ho Chi Minh City, Vietnam

ABSTRACT

Massive MIMO systems with preconfigured spatial beams efficiently serve near-field (NF) users, while far field (FF) users can be multiplexed on the same beams using non-orthogonal multiple access (NOMA). To realistically capture propagation, the spherical wave model (SWM) is employed for NF channels and the plane wave model (PWM) for FF channels, reflecting the distinct near- and far-field regions. While conventional optimization approaches such as successive convex approximation (SCA) and branch-and bound (BB) suffer from local optimality or prohibitive complexity, recent advances in deep learning have enabled scalable and adaptive solutions for wireless resource allocation. On this basis, a resource allocation strategy is developed using the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm, where the base station acts as an agent that dynamically adjusts power and allocation coefficients to maximize the sum throughput of FF users. Simulation results show that the proposed DRL based method can approach, and in some cases match, deterministic SCA at high SNR, while consistently outperforming randomly initialized SCA in medium-to-high SNR regimes. Compared to optimization-based baselines, the TD3 approach eliminates iterative problem reformulation, reduces computational complexity, and provides stronger adaptability to dynamic channels and user mobility.

KEYWORDS
Deep Reinforcement Learning, Massive MIMO, NOMA, Resource Allocation, TD3

1.INTRODUCTION

A recent advancement in non-orthogonal multiple access (NOMA) is its integration as a complementary technique into space-division multiple access (SDMA) networks, inherited from large-scale multiple-input multiple-output (MIMO) systems [1]. In this context, spatial beams are pre-configured to serve existing users and can further be reused to support additional users [2]. This reuse enhances connectivity and throughput with improved spectral efficiency and reduced computational complexity. For conventional SDMA networks operating in the far-field (FF) region—where the distance between transmitter and receiver exceeds the Rayleigh distance [3]— the application of NOMA is natural. In FF communications, beamforming is typically realized through steering vectors, forming cone-shaped beams [4]. Each beam covers a wide spatial region; thus, multiple users within the same coverage cone can share a beam via NOMA, making this approach both feasible and effective.

In contrast, near-field (NF) communications have gained increasing attention due to the use of higher carrier frequencies and large antenna arrays, which significantly extend the Rayleigh distance [5], [6]. Unlike FF systems, NF propagation requires the spherical-wave model (SWM) to capture distance-dependent phase variations. This motivates the application of beam-focusing techniques, where beams are concentrated not only in angular directions but also on specific spatial locations [7]. From this perspective, a key challenge in hybrid NF-FF scenarios is to determine how pre-configured NF beams can be effectively reused to also accommodate FF users. Addressing this challenge serves as the primary motivation of this work.

Recent works have applied optimization-based approaches such as successive convex approximation (SCA) and branch-and-bound (BB) to MIMO-NOMA systems, but these methods suffer from high complexity, sensitivity to initialization, and poor adaptability under dynamic channel conditions. In contrast, deep reinforcement learning (DRL) offers a data-driven alternative. However, existing DRL studies mainly target far-field or discrete-action models, which are inadequate for continuous hybrid NF–FF beamforming and power control. To overcome these limitations, this work introduces a TD3-based framework that enables the base station to learn continuous allocation policies directly from channel feedback without explicit modelling. The main contributions of this paper are summarized as follows:

1) A novel NF-FF Massive MIMO-NOMA architecture is introduced, exploiting preconfigured NF beams to serve additional FF users.
2) A non-convex resource-allocation problem is formulated, aiming to maximize FF throughput while satisfying NF quality-of-service (QoS) constraints.
3) A DRL-based solution using the TD3 algorithm is proposed, enabling the BS to learn continuous allocation policies from system feedback without explicit channel models.
4) Extensive simulations under realistic NF-FF channel models validate the effectiveness of the proposed framework and highlight its advantages compared with conventional optimization methods.

The remainder of this paper is organized as follows. Section II reviews related work on Massive MIMO, NOMA, and reinforcement learning in wireless systems. Section III presents the system model and problem formulation. Section IV describes the proposed DRL-based resource allocation framework. Section V provides numerical and simulation results. Section VI concludes the paper and discusses future research directions.

2. RELATED WORK

Recent studies have explored the use of machine learning (ML) and deep learning (DL) to address the high computational complexity of resource and power allocation in massive MIMO systems [8]. For example, [9] demonstrated that simple neural networks can approximate optimal power control with reduced complexity. Similarly, [10] highlighted both the effectiveness and vulnerability of DL-based power allocation, while [11] showed how DL-based optimization can enhance energy efficiency. These works confirm the potential of ML/DL in large-scale resource allocation but also reveal limitations in robustness and adaptability. Building on this trend, reinforcement learning (RL) has been increasingly adopted to tackle the dynamic nature of massive MIMO systems. [12] applied RL for adaptive scheduling, [13] used a DQN framework for beam and user grouping, and [14] employed actor-critic methods for balancing spectral and energy efficiency. These studies demonstrate the flexibility of RL beyond supervised DL approaches, particularly in handling time-varying channels and multi-objective trade-offs.

More specifically, recent work has applied RL directly to resource allocation in massive MIMO. [15] integrated DQN for joint user clustering, power allocation, and beamforming, while [16] introduced an actor-critic framework with pointer networks to reduce the action space complexity in scheduling and power allocation. Both approaches highlight the potential of RL to approximate near-optimal performance with significantly lower complexity. Despite these contributions, prior studies largely focus on either scheduling or power allocation in far-field conditions, often with simplified assumptions. Works such as [15] remain constrained by discretized action spaces, whereas [16] does not consider hybrid near-field and far-field propagation. To address these gaps, our work develops a Twin Delayed Deep Deterministic Policy Gradient (TD3)-based framework for joint beam and power allocation in hybrid NF-FF massive MIMO-NOMA systems. By reusing pre-configured near-field beams for far-field users, the proposed approach ensures both scalability and efficiency, outperforming existing methods in dynamic scenarios. Recent studies such as [14] and [15] further improved DRL-based MIMO optimization but still focused on far-field scenarios. Unlike these works, our TD3-based framework jointly handles beam and power allocation under hybrid NF–FF propagation, offering stable learning with continuous action control.

3. SYSTEM MODEL
3.1. Massive MIMO
Considering the pure spectral efficiency according to Shannon’s theory – which forms the basis for (3.1) and (3.2) – it can be shown that, in conventional Multiuser MIMO systems, choosing the number of transmit antennas M approximately equal to the number of users K is optimal: increasing M beyond that yields only logarithmic throughput growth, while the computational complexity increases linearly with M. Massive MIMO marks a significant departure from traditional Multiuser MIMO systems. Instead of attempting to operate close to the Shannon limit, it deliberately operates at a larger distance from that limit, but paradoxically achieves superior performance compared with any conventional Multiuser MIMO system.

There are three fundamental differences between Massive MIMO and conventional Multiuser MIMO systems.
1) Only the base station (BS) learns the channel matrix H .
2) The number of antennas at the BSM is typically much larger than the number of users K , although this is not strictly required.
3) Simple linear signal processing techniques are used for both uplink and downlink.

These properties enable Massive MIMO to scale effectively with the number of BS antennas M .

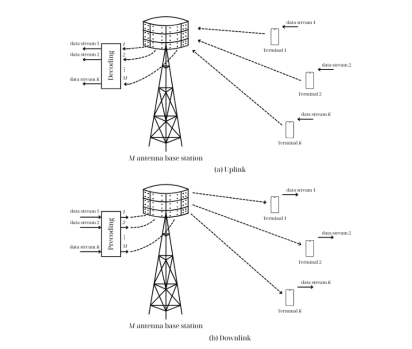
Figure 1 illustrates the basic configuration of a Massive MIMO system. Each BS is equipped with a large number of antennas M and serves a cell with many user equipments (UEs) K . UEs are usually equipped with a single antenna. Different BSs serve different cells, and except for mechanisms such as power control or pilot allocation, Massive MIMO systems do not employ cooperation between BSs. In both uplink and downlink, all UEs simultaneously use the entire time-frequency resources. On the uplink, the BS must recover the separate signals transmitted from UEs. On the downlink, the BS must ensure that each UE only receives its own intended signal. Multiplexing and demultiplexing at the BS are realized by exploiting the large number of antennas and the availability of channel state information (CSI).

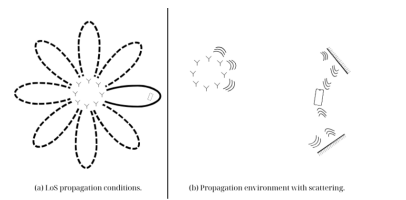
Figure 2 illustrates how precoding operates under different propagation conditions. In line-ofsight (LoS) environments, the base station (BS) forms a dedicated narrow beam for each user, with beamwidth decreasing as the number of antennas increases. Under local scattering, the received signal results from the superposition of many reflected and scattered paths, which can combine constructively at the user location when the carrier is properly chosen. Larger antenna arrays thus enable more precise energy focusing.

Figure 1. Massive MIMO systems

Figure 2. Effect of Precoding in Various Wireless Propagation Environments

Accurate channel state information (CSI) is crucial for such focusing. In time-division duplexing (TDD) systems, the BS estimates CSI from uplink pilots and exploits channel reciprocity, requiring only hardware calibration rather than absolute phase alignment. Increasing the number of antennas always reduces transmit power, allows simultaneous service to more users, and enhances spectral efficiency. Furthermore, Massive MIMO benefits from channel hardening, where small-scale fading effects vanish as M grows, making the effective channel approximate an AWGN channel. This property simplifies signal processing and allows standard modulation and coding schemes to be applied effectively.

3.2. Massive MIMO-NOMA with Coexisting Near-Field and Far-Field Communications

Consider a traditional SDMA downlink network where a base station (BS) employs a uniform linear array (ULA) with N antenna elements to serve M near-field (NF) users, each equipped with a single antenna, under the condition M N . In this study, it is assumed that M spatial beamforming vectors, denoted as pm , are pre-configured to individually serve the NF users. The objective is to further support K far-field (FF) users by reusing these pre-configured NF beams.

4. CONVENTIONAL OPTIMIZATION METHODS FOR THE RESOURCEALLOCATION PROBLEM

To address the problems of power allocation and beamforming design in MIMO-NOMA systems, classical optimization methods such as Successive Convex Approximation (SCA) and Branchand-Bound (BB) [15] are employed. These two analytical techniques are used to obtain global and approximate optimal solutions, serving as benchmarks for performance comparison with modern approaches such as deep reinforcement learning.

4.1. Rationale for Choosing SCA and BB as Baselines

SCA: A widely use approximation technique for solving nonlinear problems by sequentially approximating them as convex problems and solving them with convex optimization methods.
• BB: A technique for finding the global optimal solution in small-scale (or special) cases, commonly used to evaluate the performance upper bound.

4.2. Successive Convex Approximation (SCA) Method

Principle of SCA: SCA is based on replacing nonlinear functions with convex approximations (typically linear or tightly convex functions). At each iteration:
1. Take a reference point from the current solution.
2. Linearize the nonlinear functions or non-convex constraints.
3. Solve the approximated convex problem.
4. Update the solution and repeat until convergence.

4.3. Branch-and-Bound (BB) Method

BB is employed to obtain the global optimal solution for two special cases:
1. Case K =1 : only one FF user.
2. Case1 Dx = : each FF user is assigned to only one beam

Principle of BB:
• Define the initial solution space.
• Partition this space into subregions (branching).
• For each subregion, compute: UB D LB D ( ) upper bound, ( ) lower bound = =
• If best UB D LB ( )  , discard the subregion.
• Stop when the gap UB LB − .

Characteristics:
• BB guarantees finding the global optimal solution.
• The complexity increases exponentially with the number of variables, making it practical only for small K or special cases.

5. REINFORCEMENT LEARNING-BASED RESOURCE-ALLOCATION OPTIMIZATION

5.1. Formulation of the Resource-Allocation Problem as an MDP and Selection of the TD3 Algorithm
5.1.1. Formulation of the Resource-Allocation Problem as an MDP

To address the above Resource Allocation problem, we formulate it as a Markov Decision Process (MDP) and apply Twin Delay Deep Deterministic Policy Gradient (TD3) for this problem. The Resource Allocation problem in MIMO-NOMA systems modelled as MDP which allow take advantage of Deep Reinforcement Learning (DRL) to solve complex optimization problems, without closed-form target function. In this MIMO-NOMA system, the MDP is defined as a tuple with (S A P r , , , ) , where:

5.1.2. Selection of the TD3 Algorithm

The above problem is modelled as an MDP with both state and action spaces being continuous, non-convex, and even non-linear, under complex system dynamics (due to multipath, fading, and channel variations). 

5.2. Proposed TD3 Algorithm

We use the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm to solve the formulated MDP. For continuous control issues like beamforming and power allocation in MIMO-NOMA systems, TD3 is especially well-suited. Through three main approaches, the algorithm enhances learning performance and stability: (i) target policy smoothing to lessen sensitivity to strong Q-value peaks; (ii) double Critics to decrease overestimation bias; and (iii) delayed policy updates to stabilize Actor learning. Algorithm 3 provides a summary of the comprehensive training process.

6. NUMERICAL AND SIMULATION RESULTS

6.1. Simulation Setup

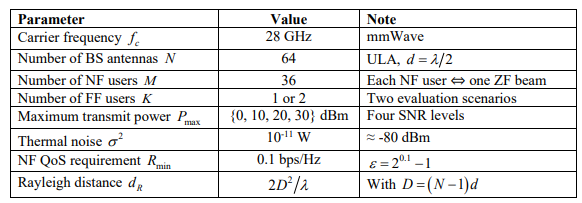
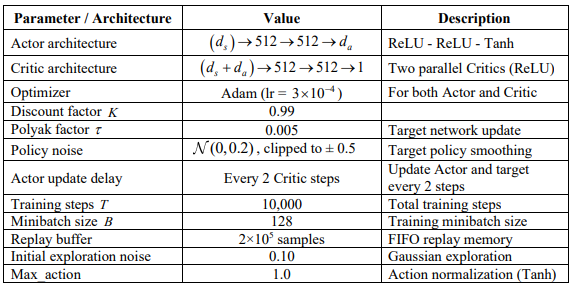
In this section, we present the simulation setup and discuss the obtained results. The simulation framework was implemented in Python 3.10 using TensorFlow 2.x and NumPy. Each experiment was executed on an Intel Core i7-10850H with GPU Quadro P620. The TD3 agent was trained using a replay buffer with random sampling and mini-batch gradient updates. The system-level parameters of the considered Massive MIMO-NOMA system, including carrier frequency, antenna configuration, number of users, power levels, and noise assumptions, are summarized in Table 1. Furthermore, the training hyperparameters and neural network architecture of the proposed TD3-based algorithm are reported in Table 2. These configurations ensure reproducibility of all results and provide a fair basis for performance comparison with conventional optimization methods.

Table 1. System parameters of the Massive MIMO-NOMA simulation.

Table 2. Training hyperparameters and TD3 architecture.

The above parameters ensure reproducibility of all results. In particular, the 512-512 Actor/Critic network architecture is selected based on empirical tuning, enabling TD3 to converge quickly without significantly increasing the online inference complexity

6.2. Analysis of the DRL Training Process

To examine the convergence and stability of the TD3 algorithm, we monitor (i) the average reward and (ii) the Actor/Critic loss functions over 10,000 training steps.
Scenario K =1, 1

Figure 3 illustrates the convergence of the reward curve of TD3 with a smoothing window of w = 300. This smoothed curve highlights the underlying trend of performance improvement, filtering out short-term fluctuations, thus offering a more reliable view of the convergence behavior.

After the initial warm-up phase (~2000 steps), the smoothed reward exhibits a clear upward trend, indicating progressive improvement of the agent’s learning process over time. Several noticeable step-like increases can be observed, each reflecting moments when the agent discovers more effective policies through exploration and exploitation. Although the per-step rewards show considerable fluctuations, the smoothed curve consistently demonstrates a positive trajectory, providing reliable evidence of stable policy enhancement.

Figure 4 illustrates the training dynamics of the Actor and Critic networks under the TD3 algorithm for the case of w = 300 , 1 Dx =. At the beginning, the Critic loss shows a sharp peak before rapidly decreasing, followed by a gradual rise to around 0.5 toward the end of training. This behavior indicates that the Critic learns quickly but begins to experience noise or mild overfitting as training progresses. In contrast, the Actor loss steadily decreases and remains relatively stable at a low level, reflecting that the Actor gradually acquires a more effective policy. The smoothness of the Actor loss curve, without significant oscillations, further confirms the stability of the policy updates throughout the training process.

The relationship between reward and loss is evident as the reward sharply increases from ~2.2 to above 5.5 once the initial spike in the Critic loss disappears and both losses stabilize, and although the Critic loss does not continue to decrease further, the reward remains high and stable because the Actor directly optimizes the expected rather than depending on the Critic’s meansquared error converging to zero. This interplay explains both the step-like jumps in reward and the final plateau observed in figure.
Scenario K = 2 , 1

In Figure 5, after the warm-up phase (around step 2000), the smoothed reward increases steadily, reflecting the progressive improvement of the agent’s learning process. Several noticeable steplike jumps can be observed, each corresponding to the discovery of more effective policies through the exploration-exploitation trade-off. Following this stage, the reward gradually converges to a relatively high and stable plateau toward the end of training. Although the per-step rewards exhibit considerable fluctuations, the smoothed curve consistently demonstrates a clear upward trend, providing reliable evidence of convergence. Figure 6 illustrates training losses of the Actor and Critic networks for the case K = 2 , 1 Dx = .

The Critic loss shows a very high initial spike (peak ≈ 11) but quickly drops to below 0.1, then gradually increases with small fluctuations and stabilizes within a narrow range of about 0.5 – 2.3 toward the end of training. This indicates that the Critic converges rapidly but may experience mild noise or overfitting during extended training. Meanwhile, the Actor loss decreases steadily from around −4 to approximately −7.5 to −7.8. Because the optimization objective is actor  = −[ ( , ( ))] Q s s , this downward trend (more negative values) reflects that the estimated Q s s ( , ( )) increases, demonstrating continuous policy improvement. The smooth trajectory of the Actor loss, without strong oscillations, further indicates stable and reliable policy updates throughout the training process.

Once the initial spike of the Critic loss vanishes and both critics stabilize at low levels (after a few tens of steps), the reward exhibits a sharp step-like increase. This indicates that a stable Q -value estimation enables more effective policy updates for the Actor network. In the later stages, even though the Critic loss shows a slight upward drift – mainly due to changing temporal difference targets as the policy evolves – the Actor loss continues to decrease into deeper negative values. Consequently, the reward keeps increasing and then maintains a high level. This behavior is consistent with the TD3 mechanisms, where twin critics and delayed policy updates mitigate noise and value overestimation, thereby ensuring stable policy improvement.

Figures 3–6 show that the TD3 agent converges smoothly after approximately 10⁴ iterations, with the critic losses remaining bounded and the actor policy steadily improving. The training cost is mainly determined by critic network updates but remains manageable due to experience replay and mini-batch learning. In summary, the characteristic learning patterns of the TD3 algorithm. First, the Critic loss shows an initial spike in mean-squared error during the early updates, which quickly diminishes once the replay buffer becomes sufficiently diverse. Second, the Actor loss remains negative and steadily decreases over time, consistent with minimizing −[ ( , ( ))] Q s s  . Third, the reward curves follow a step-like trajectory with short plateaus, reflecting the delayed policy updates and the conditioning effect of the twin critics. In both scenarios, the major jumps in reward coincide with periods when the Critic stabilizes, confirming that reliable Q -value estimation is essential for effective policy improvement.

6.3. Sum-Rate Comparison of RL (TD3) and SCA Baselines

To further evaluate the effectiveness of the proposed reinforcement learning approach, this section compares the achievable sum-rate performance of TD3 against the successive convex approximation (SCA) algorithm under two initialization strategies: deterministic and random. The comparison is conducted across different transmit power levels and in both considered scenarios, providing insights into how the RL-based method performs relative to traditional optimization based baselines.

In figure 7, the deterministic SCA consistently achieves the highest sum-rate across all transmit power levels, demonstrating its strong optimization capability when initialized properly. The RLbased method (TD3) attains comparable performance to deterministic SCA at high transmit powers, while significantly outperforming the randomly initialized SCA in the low-to-medium power range. The random initialization case yields the lowest performance, especially at low power, confirming the importance of efficient optimization strategies. Overall, the RL-based approach proves to be a practical and effective solution, as it converges near-optimal performance without requiring favorable initialization. In terms of system performance, the RL-based method lags behind deterministic SCA at low and medium transmit power levels but catches up and reaches near-identical performance at high power (30 dBm), while consistently outperforming randomly initialized SCA at 10–20 dBm. This observation highlights the robustness of the learned policy, which can generalize well across different power regimes. Moreover, the RL framework offers greater scalability for dynamic or large-scale scenarios where iterative optimization methods become computationally expensive.

In Figure 8, the deterministic SCA continues to achieve the highest sum-rate at all transmit power levels, highlighting the strong effectiveness of the algorithm when initialized properly. The RLbased method (TD3) consistently outperforms the randomly initialized SCA across all power levels, with the performance gap becoming more pronounced in the high-power region (20-30 dBm). The random initialization case yields relatively low performance, and the gap with RLbased methods increases further when the number of users rises to K = 2 .

In summary, in terms of system performance, the RL-based method remains inferior to deterministic SCA across all transmit power levels but consistently outperforms randomly initialized SCA (except at 0 dBm). This demonstrates that the learned policy is meaningful and improves steadily with increasing transmit power. The sum-rate results further reveal that (i) in the low-to-medium power regime, the RL policy tends to be more rigid due to NF QoS constraints and the associated reward-penalty structure, which leads to lower performance compared with deterministic SCA; and (ii) as the transmit power increases, RL approaches – and in some cases can even match – the deterministic SCA, while clearly outperforming random initialization. This is an encouraging indication that when constraints are relaxed, the actor is able to learn near optimal allocation structures without requiring the iterative process of SCA. Overall, the RL based approach proves to be a practical solution, converging reliably even with more users and effectively overcoming the limitations of optimization algorithms under poor initialization, thereby offering a scalable and real-time alternative for next-generation Massive MIMO-NOMA systems. Future extensions may integrate meta-learning or multi-agent coordination to further enhance adaptability and scalability in practical deployments.

7. CONCLUSION AND FUTURE WORK

This work considered a conventional downlink NOMA system where spatial beams are preconfigured for near-field users, and far-field users are superimposed onto these beams through power-domain multiplexing. Under the assumptions of single-antenna users and perfect SIC, the TD3 algorithm was implemented to learn power allocation policies. Simulation results demonstrated that the proposed DRL-based approach can approach, and in some cases even surpass, the performance of SCA at high SNR, while a performance gap remains in the low-SNR regime.

Several research directions remain open. Extending to multi-antenna users with attention enhanced Actor Critic architectures can improve large channel matrix processing. Multi-agent DRL with CTDE enables scalability for many users. Online learning under imperfect CSI, aided by meta- or transfer learning, enhances robustness. These directions can further reduce the SN Rrange performance gap and advance Massive MIMO-NOMA systems resilient to channel variability, hardware impairments, and diverse service needs.

CONFLICTS OF INTEREST

The authors declare no conflict of interest.

ACKNOWLEDGEMENTS

This research is funded by University of Science, VNU-HCM under grant number ĐT-VT 2023- 02.

REFERENCES

[1] Mathews, Belcy & Muthu, Tamilarasi. (2024). Adaptive Hybrid Deep Learning Based Effective Channel Estimation in MIMO-Noma for Millimeter-Wave Systems with an Enhanced Optimization Algorithm. International journal of Computer Networks & Communications. 16. 113-131. 10.5121/ijcnc.2024.16507.

[2] Z. Ding, “NOMA Beamforming in SDMA Networks: Riding on Existing Beams or Forming New Ones?,” in IEEE Communications Letters, vol. 26, no. 4, pp. 868-871, April 2022, doi: 10.1109/LCOMM.2022.3146583

[3] R. W. Heath, N. González-Prelcic, S. Rangan, W. Roh and A. M. Sayeed, “An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems,” in IEEE Journal of Selected Topics in Signal Processing, vol. 10, no. 3, pp. 436-453, April 2016, doi: 10.1109/JSTSP.2016.2523924.

[4] Y. Zou, W. Rave and G. Fettweis, “Analog beamsteering for flexible hybrid beamforming design in mmwave communications,” 2016 European Conference on Networks and Communications (EuCNC), Athens, Greece, 2016, pp. 94-99, doi: 10.1109/EuCNC.2016.7561012.

[5] E. Björnson and L. Sanguinetti, “Power Scaling Laws and Near-Field Behaviors of Massive MIMO and Intelligent Reflecting Surfaces,” in IEEE Open Journal of the Communications Society, vol. 1, pp. 1306-1324, 2020, doi: 10.1109/OJCOMS.2020.3020925.

[6] J. Zhu, Z. Wan, L. Dai, M. Debbah and H. V. Poor, “Electromagnetic Information Theory: Fundamentals, Modeling, Applications, and Open Problems,” in IEEE Wireless Communications, vol. 31, no. 3, pp. 156-162, June 2024, doi: 10.1109/MWC.019.2200602.

[7] H. Zhang, N. Shlezinger, F. Guidi, D. Dardari, M. F. Imani and Y. C. Eldar, “Beam Focusing for Near-Field Multiuser MIMO Communications,” in IEEE Transactions on Wireless Communications, vol. 21, no. 9, pp. 7476-7490, Sept. 2022, doi: 10.1109/TWC.2022.3158894.

[8] Aljumaily, Mustafa & Li, Husheng. (2020). Mobility Speed Effect and Neural Network Optimization for Deep MIMO Beamforming in mmWave Networks. International Journal of Computer Networks and Communications. 12. 1-14. 10.5121/ijcnc.2020.12601.

[9] Z. Zhang, M. Hua, C. Li, Y. Huang and L. Yang, “Beyond Supervised Power Control in Massive MIMO Network: Simple Deep Neural Network Solutions,” in IEEE Transactions on Vehicular Technology, vol. 71, no. 4, pp. 3964-3979, April 2022, doi: 10.1109/TVT.2022.3146434.

[10] B. R. Manoj, M. Sadeghi and E. G. Larsson, “Downlink Power Allocation in Massive MIMO via Deep Learning: Adversarial Attacks and Training,” in IEEE Transactions on Cognitive Communications and Networking, vol. 8, no. 2, pp. 707-719, June 2022, doi: 10.1109/TCCN.2022.3147203

[11] T. T. Vu, H. Q. Ngo, M. N. Dao, D. T. Ngo, E. G. Larsson and T. Le-Ngoc, “Energy-Efficient Massive MIMO for Federated Learning: Transmission Designs and Resource Allocations,” in IEEE Open Journal of the Communications Society, vol. 3, pp. 2329-2346, 2022, doi: 10.1109/OJCOMS.2022.3222749

[12] Q. An, S. Segarra, C. Dick, A. Sabharwal and R. Doost-Mohammady, “A Deep Reinforcement Learning-Based Resource Scheduler for Massive MIMO Networks,” in IEEE Transactions on Machine Learning in Communications and Networking, vol. 1, pp. 242-257, 2023, doi: 10.1109/TMLCN.2023.3313988.

[13] I. Ahmed, M. K. Shahid and T. Faisal, “Deep Reinforcement Learning Based Beam Selection for Hybrid Beamforming and User Grouping in Massive MIMO-NOMA System,” in IEEE Access, vol. 10, pp. 89519-89533, 2022, doi: 10.1109/ACCESS.2022.3199760.

[14] Y. Oh, A. Ullah and W. Choi, “Multi-Objective Reinforcement Learning for Power Allocation in Massive MIMO Networks: A Solution to Spectral and Energy Trade-Offs,” in IEEE Access, vol. 12, pp. 1172-1188, 2024, doi: 10.1109/ACCESS.2023.3347788.

[15] Y. Cao, G. Zhang, G. Li and J. Zhang, “A Deep Q-Network Based-Resource Allocation Scheme for Massive MIMO-NOMA,” in IEEE Communications Letters, vol. 25, no. 5, pp. 1544-1548, May 2021, doi: 10.1109/LCOMM.2021.3055348.

[16] L. Chen, F. Sun, K. Li, R. Chen, Y. Yang and J. Wang, “Deep Reinforcement Learning for Resource Allocation in Massive MIMO,” 2021 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 2021, pp. 1611-1615, doi: 10.23919/EUSIPCO54536.2021.9616054.

[17] Z. Ding, R. Schober and H. V. Poor, “NOMA-Based Coexistence of Near-Field and Far-Field Massive MIMO Communications,” in IEEE Wireless Communications Letters, vol. 12, no. 8, pp. 1429-1433, Aug. 2023, doi: 10.1109/LWC.2023.3277469.

AUTHORS

Pham Hoai An received a B.S. degree in Electronics and Telecommunications, from the University of Science, Vietnam National University, Ho Chi Minh City (VNU-HCM). His research interests focus on new-generation wireless communications, particularly 5GAdvanced and 6G mobile networks.

Nguyen Dung received a B.S. degree with honors in Electronics and Telecommunications Engineering, specializing in Telecommunications and Networks, from the University of Science, Vietnam National University, Ho Chi Minh City (VNU-HCM). He is now an M.S. student at the same university. His research interests include telecommunication networks and the application of artificial intelligence in optimization problems for telecommunications.

Nguyen Thi Xuan Uyen obtained her Master’s degree in Electronics Engineering, specializing in Electronics, Telecommunications, and Computer Engineering, in 2023 at the University of Science, Vietnam National University, Ho Chi Minh City (VNU-HCM). She is currently a lecturer at the same university. Her current research interests include wireless communications and telecommunication systems in 5G and 6G networks.

Nguyen Thai Cong Nghia is a lecturer in the Faculty of Electronics – Telecommunications, University of Science, VNU-HCM. He received his M.Sc. degree in Electronic Engineering, speciality of Electronics, Telecommunications, and Computer from University of Science, VNU-HCM. His research interests include wireless communications and deep learning in telecommunications.

Ngo Minh Nghia obtained his Master’s degree in Electronics Engineering, specializing in Electronics, Telecommunications, and Computer Engineering, in 2023 at the University of Science, Vietnam National University Ho Chi Minh City (VNU-HCM). He is currently a lecturer at the same university. His current research interests focus on the application of machine learning in telecommunication systems for 5G and 6G networks.