IJCNC 03

PERFORMANCE OF MULTI-HOP FSO SYSTEMS
UNDER PRACTICAL CONDITIONS WITH MALAGA
TURBULENCE CHANNELS AND POINTING ERRORS

Ha Duyen Trung
Department of Communication Engineering, School of Electrical and Electronic
Engineering , Hanoi University of Science and Technology
605/C7, No.1, Dai Co Viet Street, Hanoi, Vietnam

ABSTRACT

Free Space Optical (FSO) communication offers a high-capacity solution for wireless networks, but its performance is severely degraded by atmospheric turbulence and pointing errors, particularly in multi-hop configurations. This paper investigates the performance of multi-hop FSO systems operating over Malaga fading channels, incorporating pointing errors and 32-QAM modulation under practical conditions. We derive analytical expressions and conduct Monte Carlo simulations to evaluate key performance metrics, including Bit Error Rate (BER), Symbol Error Rate (SER), and ergodic channel capacity, as functions of hop count and turbulence severity (weak, moderate, and strong). Simulation results show that BER and SER increase exponentially with hops, reaching 10−3 to 10−2 at 5 hops under strong turbulence, while capacity decreases, dropping below 3 bits/s/Hz under similar conditions. The study highlights the tradeoffs between hop count, turbulence conditions, and system reliability, offering design guidelines for optimizing multi-hop FSO networks. These findings underscore the importance of turbulence mitigation and pointing error compensation to achieve reliable high-capacity FSO communication in real-world deployments.

KEYWORDS
Multi-hop Free Space Optics, Malaga Turbulence, Pointing Errors, QAM, Performance Analysis

1. INTRODUCTION

Free Space Optical (FSO) communication has gained significant attention as a high-capacity, cost-effective solution for wireless data transmission, leveraging the unlicensed optical spectrum to achieve data rates comparable to fiber optics without the need for physical infrastructure [1]. Its applications span terrestrial last-mile access, inter-satellite links, and disaster recovery networks [2]-[4]. However, FSO systems face substantial challenges due to atmospheric turbulence and misalignment-induced pointing errors, which degrade signal quality over long distances [5], [6], [7], [8]. To address these limitations and extend communication range, multihop FSO systems have been proposed, utilizing relay nodes to segment the transmission path and improve reliability [3]. Despite their potential, the performance of multi-hop FSO systems under realistic channel conditions remains a critical area of investigation.

Atmospheric turbulence is a primary impairment in FSO that induces random fluctuations in signal intensity, modeled by various statistical distributions [11]. Among these, the Malaga distribution has emerged as a versatile and unifying framework, capable of characterizing weakto-strong turbulence regimes by incorporating both large-scale and small-scale fading effects [12]. Recent studies have adopted the Malaga model to analyze single-hop FSO systems, demonstrating its superiority over traditional Gamma-Gamma and Log-Normal models in capturing real-world turbulence statistics [13]. For multi-hop configurations, however, the complexity increases due to the cumulative impact of turbulence across multiple links, necessitating advanced analytical performance analysis.

Pointing errors, arising from mechanical vibrations, thermal expansion, or wind-induced building sway, further complicated FSO system design, particularly in multi-hop setups where precise alignment must be maintained across all nodes [14]. Recent works have quantified the impact of pointing errors on FSO performance, often integrating them into fading models to derive outage probability and bit error rate (BER) metrics [15]. For instance, Boluda-Ruiz et al. (2021) analyzed the combined effects of Malaga fading and pointing errors in single-hop FSO links, highlighting their detrimental impact on system capacity [16]. However, extending such analyses to multi-hop systems remains underexplored, with few studies addressing the interplay between fading and misalignment across multiple hops.

Modulation schemes play a pivotal role in determining the spectral efficiency and robustness of FSO systems. Quadrature Amplitude Modulation (QAM), particularly higher-order variants such as 16-QAM and 32-QAM, has been increasingly adopted to maximize data throughput in FSO links [17]. Recent research by Varotsos et al. (2022) investigated the performance of 16-QAM in single-hop FSO systems over Malaga channels, revealing trade-offs between data rate and error performance under turbulence [18]. In multi-hop scenarios, the use of QAM introduces additional challenges, as the signal-to-noise ratio (SNR) degrades with each hop, amplifying the effects of fading and pointing errors. While some studies have explored multi-hop FSO with simpler modulation schemes like On-Off Keying (OOK) [19], the application of QAM in such systems remains limited, despite its relevance to high-capacity networks.

Recent work revealed significant progress in FSO research. For example, Trinh et al. (2020) evaluated the ergodic capacity of dual-hop FSO systems under Gamma-Gamma fading with pointing errors, proposing closed-form expressions for performance analysis [20]. Similarly, Sharma and Kumar (2023) examined multi-hop FSO systems with relay selection under Malaga fading, focusing on outage probability but neglecting advanced modulation schemes [21]. These works, however, provide valuable insights; they often focus on specific aspects, such as channel modeling or relay strategies, without fully addressing the combined effects of Malaga fading channels, pointing errors, and QAM modulation in multi-hop FSO configurations. These research gaps motivate a holistic analysis to bridge theoretical modeling with practical system design.

This paper investigates the performance of multi-hop FSO systems over Malaga fading channels in the presence of pointing errors, with a focus on 32-QAM modulation. The contributions of this paper can be described as follows:

Propose the analytical framework by deriving novel closed-form and approximate expressions for key performance metrics, including BER, SER and ergodic capacity, considering the joint impact of Malaga atmospheric turbulence for weak, moderate and strong, pointing errors, and the number of multi-hop relaying under M-QAM. This framework extends beyond existing single-hop analyses and provides a unified approach for system optimization.

Perform evaluation of the designed multi-hop FSO systems under practical conditions. Through numerical simulations and parametric analysis, we quantify the trade-offs between the number of hops, various atmospheric turbulence conditions, and pointing error, offering design suggestions for deploying robust multi-hop FSO networks in practical conditions.

The remainder of this paper is structured as follows: Section 2 describes the system and channel models, Section 3 presents the analytical derivations, Section 4 discusses numerical simulation results, and Section 5 concludes the study with future research directions.

2. SYSTEM AND CHANNEL MODELS

2.1. System Model

We consider an AF multi-hop relay FSO transmission system as shown in Fig. 1, which operates over independent and not identically distributed fading channels. The source terminal S and destination terminal D can be connected using multiple optical wireless links arranged in an endto-end configuration such that the source terminal S communicates with the destination terminal D through c relaying terminals 1 2 , ,…, R R R c .

Figure 2. The source node (transmitter), relaying node (repeater) and destination node (receiver) of FSO
systems using SC-QAM signals

It is assumed that all relaying terminals concurrently receive and transmit in the same frequency band, and no latency is incurred in the whole chain of relay transmissions and there is no multihop diversity. In Fig. 2, at the transmitter of the first hop, QAM symbol is up converted to an intermediate frequency c f to generate the electrical et() . This electrical QAM signal is then used to modulate the intensity of a laser of the transmitter. Therefore, the transmitted optical intensity is [22]

where P s denotes the average optical power per symbol, k is the modulation index, and c f is the intermediate frequency. Because of atmospheric loss, atmospheric turbulence and the pointing error, the received optical intensity signal at the first relaying terminal is

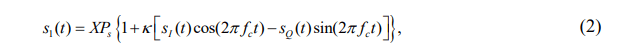
where X presents the signal scintillation caused by atmospheric lost, atmospheric turbulence and pointing errors. At each relaying terminal, an AF module is used for signal amplification. The electrical signal output of the AF module at the first relaying node is therefore expressed as

where  and PAF are the responsivity of the PhotoDetector (PD) and the AF’s amplify power, respectively. The receiver noise 1 u ()t can be modelled as an additive white Gaussian noise (AWGN) process with power spectral density 0 N .

Repeating the above process over next c hops, the output electrical signal of the PD at the D terminal is

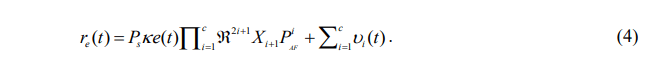
In addition, the instantaneous signal-to-noise ratio (SNR), denoted as y , at the input of the electrical demodulator of the optical receiver of the destination terminal, is defined as the ratio of the time-averaged AC photo-current power to the total noise variance.

2.2. Channel Model

As described above, X represents the optical intensity fluctuations resulting from atmospheric loss Xl , atmospheric turbulence X a , and pointing error X p , which can be described as X X X X = l a p .

2.2.1. Atmospheric Loss

Atmospheric loss Xl is a deterministic component that exhibits no randomness in its behavior, thus acting as a fixed scaling factor over a long period. It is modelled in [1] as L X e l -s = , where denotes a wavelength and weather – dependent attenuation coefficient, and L is the link distance.

2.2.2. Malaga Turbulence Fading Model

The atmosphere turbulence model is a general fading channel model of FSO. The transmitted optical signal reaching the receiver has three components of the line-of-sight (LOS) contribution UL, the coupled to LOS fading contribution C US (quasi-forward scattering fading contribution G US . Since the G US energy is dispersed to the off-axis eddies at the receiver, it is statistically independent from the two other parts. The average power of the LOS contribution UL is Ω = E[|UL| 2 ]. The average power of are C US and G US are E[| C US | 2 ] = 0 2b r and E[| C US | 2 ] = 0 2 (1 ) b – r , respectively. The average power of the total scattering is 2 2 2 E[| | | | ] 0 C G b U U = + S S . The parameter r Î[0, 1] is the amount of the scattering power coupled to UL

The Malaga probability density function (PDF) of the irradiance intensity,

The Malaga probability density function (PDF) of the irradiance intensity, X a is defined by [23]

where 2 E[| | 2 (1 ) 0 G y r = = – U b S , () K v × is the second kind of modified Bessel function with order v and a is a positive parameter related to the effective number of large-scale cells of the scattering process, b is the number of natural fading parameters related to the amount of smallscale fading parameter. The average power contributed by the given coherence is ‘ 0 0 2 2 2 cos( ) A B W = W + + W – r r j j b b , where j A and j B are the deterministic phases of the LOS fading contribution and the coupled LOS fading contribution, respectively.

The strong generalization ability of the Malaga turbulence fading model enables it to uniformly characterize various classical atmospheric turbulence effects in the analysis and design of free space optical communication systems. This model is used for a wide range of scenarios from weak atmospheric turbulence to strong atmospheric turbulence, depending on model parameters setting of a and b [14].

2.2.3. Pointing Error Fading Model

A statistical pointing error model is developed in [15]. The model assumes a circular detection aperture and a Gaussian spatial intensity profile of the beam waist radius, w z , on the receiver plane. Correspondingly, the PDF of X p is given as

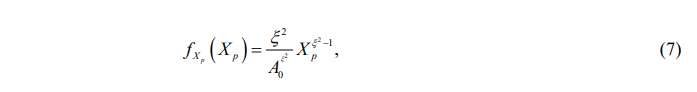
where 0 0 £ £ X A p , ( ) 2 0 A = erf( ) n is the fraction of the collected power at the radial distance of 0 (no pointing error).

The Gauss error function erf( )× is defined as 2 0 erf( ) 2 / x t x e dt p – = ò . The parameter / 2 z n p w = r with r and w z denote the aperture radius and the beam waist at the distance z, respectively. The parameter / 2 , x w s = zeq s is the ratio between the equivalent beam radius at the receiver and the pointing error displacement standard deviation, s s , at the receiver. The equivalent beam radius, w zeq , can be calculated by 2 2 erf( ) 2 exp( ) w w p n n n zeq z = – é ù ë û [15], where 1/2 2 2 0 0 1 ( / ) w w e l pw z = + é ù L ë û with w0 is the transmitter beam waist radius at z=0, and 2 2 1 / 0 0 e w r = + , ( ) 3/5 2 2 0 0.55 r C k L n – = is the coherence length.

2.2.4. The Composite Channel Model

The Malaga distribution is a generalized turbulence model, captures the combined effects of large-scale and small-scale fading, with weaker turbulence (higher a b, values) resulting in less signal attenuation and lower BER, while stronger turbulence (lower a b, values) leads to greater fading and higher error rates [23]. The cumulative impact of pointing errors across multiple hops, as modeled by the parameter x , further degrades performance by reducing the fraction of collected optical power at each relay, particularly noticeable in the steeper BER increase under strong turbulence [14].

3. ANALYTICAL DERIVATION

3.1. Error Rate

The general symbol error rate (SER) expression for evaluating the AF relaying FSO systems over the log-normal channel can be expressed by [22]

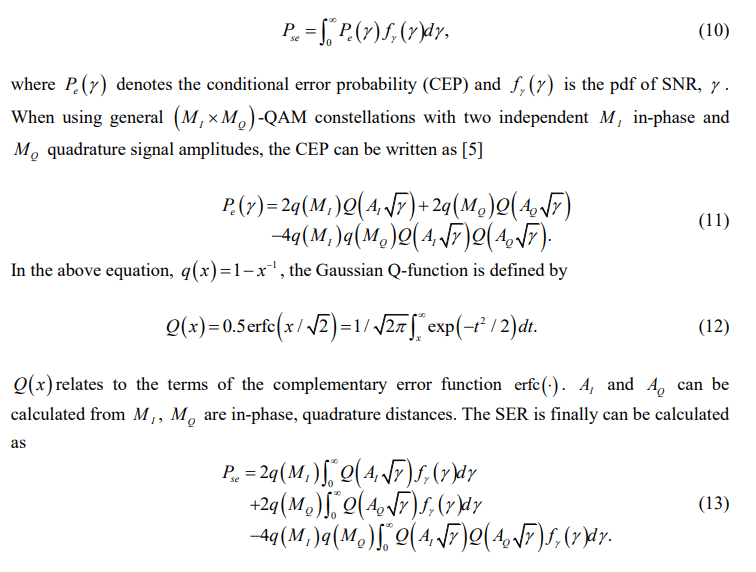
Computing this SER requires to work with integrals involving the Gaussian Q-function, which cannot be expressed in closed-form in terms of elementary functions. As a result, approximating the Gaussian Q-function in closed-form expressions with high accuracy becomes a necessity. To

3.2. Channel Capacity

The channel capacity of the designed multiple-hop FSO system represents the maximum rate at which information can be reliably transmitted over the channel, typically measured in bit/s/Hz. The ergodic capacity is the average capacity over all possible channel states, accounting for the random variations caused by atmospheric turbulence and pointing errors. It is mathematically defined as the expectation of the Shannon capacity formula as [24], [25]

where, eq g is the equivalent end-to-end SNR of the two-hop system, approximated for the AF relay as

where 1 g and 2 g are the SNRs of the first hop (Source-to-Relay) and second hop (Relay-toDestination), respectively

To compute Cerg , the PDF of eq g must be derived by combining the Malaga distribution (for atmospheric turbulence) and the pointing error model. This PDF is then integrated with the logarithmic function of log 1 2 ( +g ) . Due to the complexity of the resulting PDF, analytical solutions are often intractable, and numerical integration methods or Monte Carlo simulations are typically employed.

Since the design systems use M-QAM modulation schemes, which transmit log2(M) bits per symbol. The theoretical maximum capacity over noise-free scenarios can be expressed as

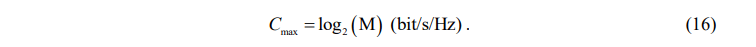
However, in practice, the presence of atmospheric turbulence, pointing errors, and noise reduces the achievable capacity. To determine the effective capacity, it must take into account the error performance of M-QAM under practical conditions. For example, in case of 32-QAM, we first calculate BER for 32-QAM in an Additive White Gaussian Noise (AWGN) channel, adjusted for the turbulence fading and pointing errors, can be approximated as

distance between constellation points in 32QAM normalized by the average energy per symbol.

The channel capacity, considering the error rate, can be calculated by adjusting the maximum capacity based on the binary entropy function as

where 2 2 H p p p p p ( ) = log ( ) (1 )log (1 ) – – – – is the binary entropy function representing the information loss due to errors. Eq. (17) presents the reliable data rate achievable with 32QAM under the given channel conditions.

4. SIMULATION RESULTS

Using the derived expressions, Equations (5), (8), (13) and (18) ( ) X f X , g , we evaluated SER, BER and channel capacity performance of the AF relaying FSO systems in the Malaga turbulence channels with effects of the pointing error displacement standard deviation. We use the MATLAB software to simulate performance for different case studies of system parameters with the number of trials for each simulation of 106 . The analysis is carried out under a variety of operating conditions by changing SNR, the number of relaying hops, modulation schemes, and atmospheric turbulence channels of Malaga distributions to the system performance evaluated by SER, BER and channel capacity. Based on the obtained results, we can evaluate and provide the most optimal parameters that the system to operate effectively. Relevant system, channel parameters and values are provided in Table 1. In the performance analysis, the laser wavelength of 1550 nm, the Photodetector responsivity of 0.8 A/W with modulation index of 1. Assuming the attenuation coefficient of 3.436 over the total link transmission distance of 2000 m using one relay station. For Malaga turbulence fading channel, considering the effective number of the scattering process of a , the amount of fading parameter of b with the average power of the LOS contribution of 1, the transmitter beam waist radius of 5×10-3 m and the pointing error displacement standard deviation of 0.05.

Table 1. System and channel parameters.

Figure 3 illustrates the Symbol Error Rate (SER) performance as a function of the average Signal-to-Noise Ratio (SNR) for two Free-Space Optical (FSO) communication configurations of multi-hop FSO (2 × 1000m) (blue dashed line) and direct FSO (2000m). We can observe that the direct FSO system demonstrates a steeper decline in SER as SNR increases, indicating better performance at higher SNR values. Whereas the multi-hop FSO system exhibits a higher SER across the entire SNR range, suggesting that the relaying approach does not significantly mitigate channel impairments in this scenario. In addition, while multi-hop relaying is often expected to improve performance by shortening the transmission distance per hop, in this case, it does not show a noticeable advantage. The reason could be attributed to additional noise accumulation at the relay, increased pointing errors, or other impairments introduced by the relaying process. Moreover, in the SNR threshold behavior of low SNR (<10 dB), the performance difference between the two systems is relatively small, as experience high SER. Whereas, at higher SNR (>15 dB), the direct FSO system significantly outperforms the multi-hop system, achieving much lower SER values. This suggests that at sufficient power levels, a single long-distance transmission is more beneficial than breaking the link into multiple shorter segments.

The results indicate that a direct FSO link outperforms a two-hop system for the given conditions, particularly at higher SNR values. While multi-hop FSO can be beneficial in scenarios with extreme attenuation or blockage, its effectiveness depends on factors such as relay noise, pointing errors, and turbulence. Further optimization, such as adaptive power allocation or intelligent relay placement, may enhance the benefits of multi-hop transmission.

Figure 3. SER performance in multi-hop and direct FSO systems in moderate turbulence channel and pointing errors

Figure 4 evaluates the channel capacity of the two-hop FSO communication system operating over a Malaga turbulence channel, considering pointing errors. This analysis focuses on a 32- QAM modulation scheme while varying the SNR from 0 to 20 dB. The comparison includes two transmission scenarios. Firstly, in two-hop FSO (2×1000m), a relay-assisted transmission is used where the total distance is split into two equal segments of 1000m each. Secondly, in direct FSO (with L=2000m), a direct transmission spanning 2000m without a relay. It can be observed from Figure 4 that channel capacity grows with SNR as expected, the channel capacity increases monotonically with SNR. Higher SNR values improve the signal quality received, leading to enhanced spectral efficiency. The capacity shows near-linear growth at lower SNR, however, it gradually tapers off at higher SNR values due to the diminishing impact of additional power in high-turbulence environments. It can also observe that the impact of multi-Hop vs. direct transmission in the comparison between two-hop and direct FSO transmission reveals a notable difference in channel capacity. Direct transmission consistently achieves higher capacity across all SNR values. This outcome aligns with theoretical expectations since the introduction of a relay node results in additional signal processing delays, potential misalignment, and turbulence effects at each relay point, which slightly reduce overall efficiency. In the low SNR region (0–10 dB), the capacity gap between the two schemes is relatively small. This is because noise dominates the system, and the benefits of multi-hop transmission in mitigating turbulence are not yet significant. However, in the high SNR region (10–20 dB), the direct FSO system outperforms the two-hop FSO system more clearly. The increased power allows direct transmission to

overcome turbulence effects more efficiently, whereas the relay-based system still incurs additional impairments from each relay hop.

The observed capacity trends align with Shannon’s capacity theorem, where the ergodic capacity is given by eq. (13). The Malaga fading model, incorporating both large-scale and small-scale turbulence, captures the stochastic nature of atmospheric impairments, with weaker turbulence (higher α, β) preserving higher capacity due to less severe fading, while stronger turbulence (lower α, β) reduces capacity through increased signal variability [1]. Pointing errors further exacerbate this degradation by introducing additional power loss, particularly pronounced in multi-hop configurations where alignment must be maintained across multiple links [4]

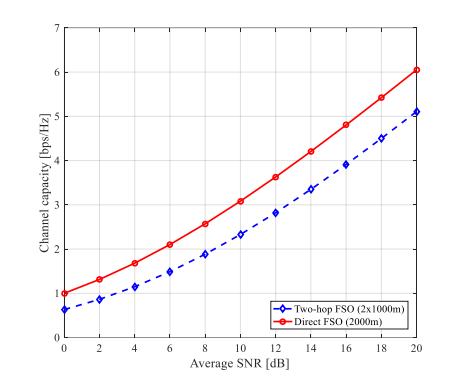
Figure 4. Channel capacity vs. average SNR for two-hop and direct FSO systems in Malaga channel with pointing error, s s =0.1.

The Figure 5 illustrates the Bit Error Rate (BER) performance of a multi-hop FSO communication system as a function of the number of hops, the link length L = 1000 m operating under Malaga fading channels with pointing errors x =1.5 and 32-QAM modulation at a fixed SNR of 20 dB. The results are presented for three turbulence scenarios of weak, moderate, and strong atmospheric turbulence fading, characterized by the Malaga distribution parameters: {a b = = 4.0, 3.0} for weak turbulence, {a b = = 2.5, 2.0} for moderate turbulence, and {a b = = 1.5, 1.0} for strong turbulence channels. Across all turbulence conditions, the BER increases monotonically with the number of hops, ranging from 1 to 5. This trend is expected in multi-hop FSO systems employing AF relaying, as each additional hop introduces cumulative fading and noise, degrading the end-to-end SNR and thus elevating the error rate. For instance, at 1 hop, the BER is on the order of 10−5 to 10−4, while at 5 hops, it escalates to 10−3 to 10−2 , depending on turbulence strength.

It can also be seen from Figure 5 that; the weak turbulence scenario exhibits the lowest BER across all hop counts. At 1 hop, the BER is approximately 10−5, increasing to around 10−3 at 5 hops. This reflects minimal atmospheric distortion, likely corresponding to higher a b, values (e.g., a b = = 4.0, 3.0 ), indicating less severe fading. In the moderate turbulence: The orange curve shows an intermediate BER performance, with a starting value near 10−4 at 1 hop, rising to approximately 10−2 at 5 hops. This suggests moderate fading effects, possibly with a b = = 2.5, 2.0 , where both large-scale and small-scale turbulence contribute significantly. Finally, for strong turbulence, starting at about 10−4 at 1 hop and reaching nearly 10−2 at 5 hops. This indicates severe atmospheric turbulence, likely associated with lower a b, values (e.g., a b = = 1.5, 1.0 ), leading to substantial signal degradation.

The presence of pointing errors, as modeled in the simulation, further exacerbates the BER, particularly with increasing hops. The use of 32-QAM, a high-order modulation scheme transmitting 5 bits per symbol, is inherently more susceptible to noise and fading compared to lower-order schemes like QPSK. The fixed SNR of 20 dB is insufficient to maintain low BER under strong turbulence and multiple hops, highlighting the trade-off between spectral efficiency and reliability in FSO systems.

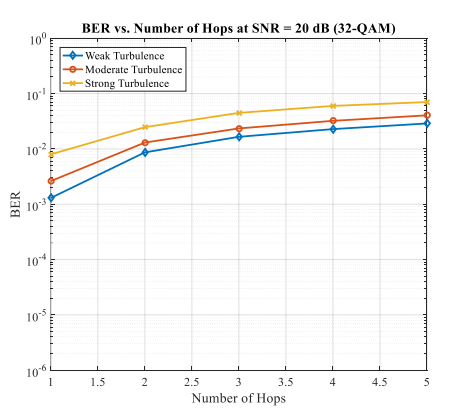
Figure 5. BER vs. number of FSO hops for various turbulence channel conditions with pointing error x =1.5 at the fixed SNR = 20 dB, link length L = 1000 m, using the 32-QAM modulation scheme.

The results from Figure 5 suggest a practical limit on the number of hops, particularly under strong turbulence, where BER exceeds 10-3 at 5 hops. For reliable communication (e.g., BER 10- 6 ), a single-hop or dual-hop configuration may be preferable, depending on turbulence conditions. Strategies such as adaptive optics, diversity techniques, or forward error correction could mitigate turbulence effects, especially in strong conditions. Adjusting pointing error through improved tracking systems could also enhance performance. While 32-QAM offers high spectral efficiency, its sensitivity to noise and fading under multi-hop FSO conditions indicates that lower-order modulation (e.g., 16-QAM or QPSK) might be more robust for longer hop counts or severe turbulence, albeit at reduced data rates. The capacity reduction with increasing hops is attributed to the cumulative effect of fading and noise amplification in AF relaying, where the equivalent SNR is approximated by the minimum or harmonic mean of individual hop SNRs, scaled to the input SNR. At 20 dB SNR, the system operates near the threshold for reliable high-order modulation, and the capacity drops under strong turbulence and multiple hops highlights the trade-off between range extension (via hops) and spectral efficiency.

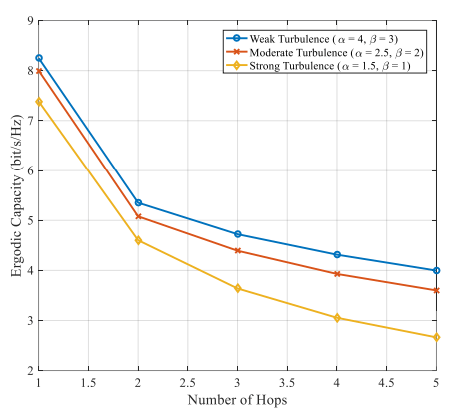
The Figure 6 presents the ergodic channel capacity (bits/s/Hz) of a multi-hop FSO communication system as a function of the number of hops, ranging from 1 to 5, under Malaga fading channels with pointing errors and 32-QAM modulation at a fixed SNR of 20 dB. The results are depicted for three turbulence scenarios of weak, moderate, and strong turbulence channels, characterized by the Malaga distribution parameters a b, .

In all turbulence conditions, the ergodic capacity decreases monotonically with the number of hops. This is consistent with the theoretical behavior of multi-hop FSO systems using AF relaying, where each additional hop introduces cumulative fading, pointing errors, and noise amplification, reducing the effective end-to-end SNR and thus the achievable capacity. For instance, at 1 hop, the capacity ranges from approximately 8.5 bits/s/Hz (weak turbulence) to 6 bits/s/Hz (strong turbulence), but at 5 hops, it drops significantly to around 5 bits/s/Hz (weak) and 2.5 bits/s/Hz (strong).

In the impact of turbulence strengths. The weak turbulence scenario exhibits the highest capacity across all hop counts. At the 1 st hop, the capacity is approximately 8.5 bits/s/Hz, decreasing to about 5 bits/s/Hz at the 5 th hops. This reflects minimal atmospheric turbulence, likely corresponding to higher a b, values (4.0, 3), resulting in less signal attenuation and higher SNR. The moderate turbulence starts at around 7.5 bits/s/Hz at 1 hop and declines to approximately 3.5 bits/s/Hz at 5 hops. This indicates moderate fading effects, possibly with a = 2.5, b = 2, where both large-scale and small-scale turbulence contribute to capacity reduction. The strong turbulence begins at about 6 bits/s/Hz at 1 hop and falls to around 2.5 bits/s/Hz at 5 hops. This reflects severe atmospheric turbulence, likely associated with lower a b, values (1.5, 1), leading to significant signal degradation and capacity loss.

The results from Figure 6 also indicate a practical limit on the number of hops, especially under strong turbulence, where capacity falls below 3 bits/s/Hz at 5 hops. For applications requiring high data rates (e.g., >5 bits/s/Hz), a single-hop or dual-hop configuration is recommended under weak-to-moderate turbulence, with careful consideration of pointing error mitigation. Techniques such as adaptive optics, aperture averaging, or diversity schemes could mitigate turbulence effects, particularly in strong conditions, potentially increasing capacity. Enhancing pointing accuracy (e.g., increasing ξ through advanced tracking systems would also reduce capacity loss. While 32-QAM maximizes spectral efficiency, its performance under severe fading and multiple hops suggests that lower-order modulation (e.g., 16-QAM or QPSK) might be more suitable for longer multi-hop links, sacrificing capacity for reliability [9], [10].

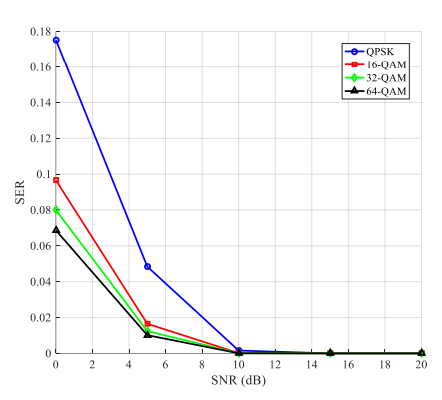
Figure 7. SER vs. SNR in Malaga turbulence channel with pointing error for various modulation schemes.

Results in Figure 7 investigates the SER and channel capacity performance in FSO communication systems over the Malaga turbulence channel, considering pointing errors. The system performance is analyzed under different modulation schemes, including QPSK (4-QAM), 16-QAM, 32-QAM, and 64-QAM, while varying the SNR from 0 to 20 dB.

The SER results exhibit a downward trend as SNR increases, indicating improved system reliability. The impact of modulation order on SER is evident, with higher-order QAM schemes suffering from higher SER values due to their reduced Euclidean distance between constellation points. QPSK demonstrates the lowest SER across all SNR values, followed by 16-QAM, 32- QAM, and 64-QAM, which progressively show higher error rates. This aligns with theoretical expectations, as higher-order modulations require stronger SNR to maintain comparable reliability. Additionally, the presence of pointing errors introduces a degradation in SER performance. The pointing error model, incorporating beam divergence and atmospheric fluctuations, reduces the effective SNR, leading to a higher probability of symbol errors. This effect is more pronounced at lower SNR values, where the system is already susceptible to noise and turbulence.

5. CONCLUSIONS

This study has comprehensively evaluated the performance of multi-hop Free Space Optical (FSO) systems under realistic conditions, focusing on Malaga fading channels with pointing errors and 32-QAM modulation. Through analytical derivations and Monte Carlo simulations, we analyzed key performance metrics of Bit Error Rate (BER), Symbol Error Rate (SER), and ergodic channel capacity, as functions of hop count and turbulence severity (weak, moderate, and strong). The results reveal that BER and SER increase exponentially with the number of hops, reaching 10-3 to 10-2 at 5 hops under strong turbulence, reflecting the cumulative impact of atmospheric fading and pointing errors on system reliability. Conversely, ergodic channel capacity decreases significantly with increasing hops, dropping below 3 bits/s/Hz under strong turbulence at 5 hops, highlighting the trade-off between range extension and spectral efficiency. These findings underscore the critical challenges posed by atmospheric turbulence and misalignment in multi-hop FSO systems, particularly for high-order modulation schemes like 32- QAM. The study provides valuable design guidelines, suggesting that hop counts should be limited (e.g., to 1–2 hops) under strong turbulence to maintain acceptable BER/SER levels and capacity. Future research should explore advanced mitigation techniques, such as adaptive optics, diversity schemes, or hybrid RF/FSO systems, to enhance performance under severe conditions. Furthermore, the analysis could be extended to advanced relay strategies (e.g., Decode-andForward) to improve capacity. Experimental validation in practical FSO conditions under various atmospheric turbulence conditions would complement simulation results.

CONFLICT OF INTEREST

The authors declare no conflict of interest

ACKNOWLEDGEMENTS

The authors would like to thank reviewers.

REFERENCES

[1] H. Kaushal and G. Kaddoum, “Optical communication in space: Challenges and mitigation techniques,” IEEE Communications Surveys & Tutorials, vol. 19, no. 1, pp. 57–96, 2017.

[2] K. Majumdar; Z. K. Ghassemlooy, and A. A. Bazil Raj. Principles and Applications of Free Space Optical Communications. IET, ISBN: 978-1-78561-415-6, 2019, 500pages.

 [3] B. C. Dike, C. M. Akujuobi and S. Alam, “A Comparative Study of Cooperative and Noncooperative Wideband Spectrum Sensing in Cognitive Radio Networks for 5G Applications,” The International Journal of Computer Networks & Communications (IJCNC), vol. 16, no. 6, 2024, pp. 1-19.

[4] S. A. Al-Gailani, M. F. M. Salleh, A. A. Salem, R. Q. Shaddad, U. U. Sheikh, N. A. Algeelani, and T. A. Almohamad, “A survey of free space optics (FSO) communication systems, links, and networks,” IEEE Access, 9, pp. 7353-7373, 2020.

[5] A. A. Farid and S. Hranilovic, “Outage capacity optimization for free-space optical links with pointing errors,” Journal of Lightwave Technology, vol. 25, no. 7, pp. 1702–1710, 2007.

[6] H.D. Trung, “Performance of UAV-to-Ground FSO Communications with APD and Pointing Errors,” Appl. Syst. Innov., vol. 4, no. 3, 2021, 65.

[7] M. Safari and M. Uysal, “Relay-assisted free-space optical communication,” IEEE Transactions on Wireless Communications, vol. 7, no. 12, pp. 5441–5449, 2008.

[8] D.H. Ai, H.D. Trung, and D.T. Tuan, “On the ASER Performance of Amplify-and-Forward Relaying MIMO/FSO Systems Using SC-QAM Signals over Log Normal and Gamma-Gamma Atmospheric Turbulence Channels and Pointing Error Impairments,” Journal of Information and Telecommunication (TJIT), vol. 4, no. 3, pp. 1-15, 2020.

[9] H.D. Trung and N.H. Trung, “Relay UAV-Based FSO Communications over Log-normal Channels with Pointing Errors,” 20th the International Conference on Intelligent Systems Design and Applications (ISDA), Volume 1351 of the Advances in Intelligent Systems and Computing series, December 12-15, 2020.

[10] H.D. Trung, “Performance Analysis of Amplify-and-Forward Relaying FSO/SC-QAM Systems over Weak Turbulence Channels and Pointing Error Impairments,” Journal of Optical Communications (JOC), Volume 39, Issue 1, Jan. 2018, pp. 93–100.

[11] H. Kaushal, V.K. Jain, S. Kar, “Free-Space Optical Channel Models,” In: Free Space Optical Communication. Optical Networks, Springer, https://doi.org/10.1007/978-81-322-3691-7_2, 2017.

[12] A. Jurado-Navas, J. M. Garrido-Balsells, J. F. Paris, and A. Puerta-Notario, “A unifying statistical model for atmospheric optical scintillation,” in Numerical Simulations of Physical and Engineering Processes, IntechOpen, 2011, pp. 181–206.

[13] I. E. Lee, Z. Ghassemlooy, and W. P. Ng, “Effects of aperture averaging and beam width on a partially coherent Gaussian beam over Malaga turbulence channels,” Optics Communications, vol. 427, pp. 543–550, 2018.

[14] W. Gappmair, S. Hranilovic, and E. Leitgeb, “Performance of PPM on terrestrial FSO links with turbulence and pointing errors,” IEEE Communications Letters, vol. 14, no. 5, pp. 468–470, 2010.

[15] H. AlQuwaiee, I. S. Ansari, and M.-S. Alouini, “On the performance of free-space optical communication systems with pointing errors,” IEEE Transactions on Wireless Communications, vol. 14, no. 8, pp. 4279–4292, 2015.

[16] R. Boluda-Ruiz, A. García-Zambrana, and C. Castillo-Vázquez, “Unified performance analysis of FSO links over Malaga turbulence with pointing errors,” Journal of Optical Communications and Networking, vol. 13, no. 6, pp. 123–134, 2021.

[17] M. R. Bhatnagar and Z. Ghassemlooy, “Performance analysis of QAM-based FSO systems over atmospheric turbulence channels,” IEEE Photonics Technology Letters, vol. 27, no. 12, pp. 1305– 1308, 2015.

[18] G. K. Varotsos, H. E. Nistazakis, and G. S. Tombras, “16-QAM over FSO with Malaga turbulence: Performance evaluation under foggy conditions,” Optics Express, vol. 30, no. 4, pp. 5678–5692, 2022.

[19] C. Abou-Rjeily and A. Slim, “Cooperative diversity for free-space optical communications: Transceiver design and performance analysis,” IEEE Transactions on Communications, vol. 59, no. 3, pp. 658–663, 2011.

[20] P. V. Trinh, T. V. Pham, and A. T. Pham, “Ergodic capacity of dual-hop FSO systems over GammaGamma fading with pointing errors,” IEEE Access, vol. 8, pp. 12345–12356, 2020.

 [21] S. Sharma and N. Kumar, “Multi-hop FSO systems with relay selection over Malaga fading channels,” IEEE Transactions on Vehicular Technology, vol. 72, no. 2, pp. 1890–1902, 2023.

[22] H. D. Trung, D. T. Tuan, Anh T. Pham, “Pointing error effects on performance of free-space optical communication systems using SC-QAM signals over atmospheric turbulence channels,” AEU – International Journal of Electronics and Communications, vol. 68, no. 9, 2014, pp. 869-876.

[23] D. Chen, L. Tang, M. Wang, and Y. Liu, “Performance analysis of MIMO FSO adaptive mode switching in Malaga turbulent channels with pointing error,” Optics and Laser Technology, vol. 181 (2025), pp. 111967, 2025.

[24] C. E. Shannon, “A mathematical theory of communication,” Bell System Technical Journal, vol. 27, no. 3, pp. 379–423, 1948.

[25] P. Poornima, G. Laxminarayana and D. Srinivas Rao, “Performance Analysis of Channel Capacity and Throughput of LTE Downlink System,” International Journal of.

AUTHORS

Ha Duyen Trung studied the B.Eng. degree in Electronics and Telecommunications from Hanoi University of Science and Technology, Vietnam from 1998 to 2023 and the MSc. and PhD. degree in Communications Engineering from Chulalongkorn University, Bangkok, Thailand from 2003 to 2009. He has been a lecturer and researcher at the School of Electronics and Telecommunications from 2009 to 2021 and at the School of Electrical and Electronic Engineering since 2021, Hanoi University of Science and Technology. He is now an Associate Professor at the same University. From 2007 to 2008 he was a research student at the mobile communication research group of Tokyo Institute of Technology, Japan. In 2012, Dr. Trung was a visiting researcher at the University of Aizu, Japan. His present research interests are in the areas of signal processing and information theory in optical wireless communications and systems including free-space optics and visible light communications.