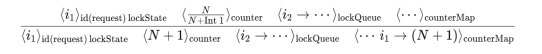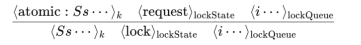IJCNC 01

FORMAL ABSTRACTION & INTERFACE LAYER FOR APPLICATION DEVELOPMENT IN AUTOMATIONFOCUSSED DISTRIBUTED SYSTEMS

Vivek Ramji , Sr. Software Engineer, Microsoft

ABSTRACT

This paper presents a novel, formal language semantics and an abstraction layer for developing application code focussed on running on agents or nodes of a multi-node distributed system aimed at providing any IoT service, automation, control or monitoring in the physical environment. The proposed semantics are rigorously validated by K-Framework alongside a simulation with code produced using the said semantics. Furthermore, the paper proposes a clocking strategy for systems built on the framework, potential conflict resolution designs and their trade-offs, adherence to CAP Theorem and verification of the atomic semantic using Fischer’s Protocol. A negative test-case experiment is also included to verify the correctness of the atomic semantic.

KEYWORDS

Distributed System, Asynchronous Clocking, Conflict Resolution, Race Condition, K-Framework, Language Semantics, PCCL, Automation, IoT

1.INTRODUCTION

Distributed applications that monitor and control the physical environment have gained prominence with the rise of supply chain management [1], [2], factory automation [3], and Internet of Things (IoT). While new capabilities and systems are deployed routinely, testing, debugging, and formal verification remain monumental [4]. Part of the challenge arises from the fact that the current language abstractions [5], [6] are inherited from those that are used for developing standalone applications and do not provide any abstractions for programming opendistributed systems that monitor and control the physical environment.

Aiming to gain insight about some of these challenges, we are developing a programming system for distributed heterogeneous robotics. In this paper, we present the design of an abstraction layer written in PCCL and its formal semantics. The language provides abstractions for distributed computational nodes or agents to interact with each other and with the physical environment. The user writes code for a single agent, which can be deployed on multiple (possibly heterogeneous) agents to perform a distributed task, such as leader election, formation, distributed search, and distributed SLAM [7]. PCCL provides a precondition-effect style of programming,

Control variables change when the external functions are called, corresponding to the continuous trajectory of the HIOA, and this takes non-zero time to occur.

We introduce a time model in Section 3 which guards against zeno behavior of the applications. We designed the semantics of this language, driven by one simple idea. The effect of the interaction with the physical environment is seen only on “control” variables, or variables which are controlled outside the environment and provided controllers to determine the values of these variables when looked up. The semantics of this language can be specified independently, considering these controllers as external functions which return values for these variables. We provide several abstractions to the user for communication and physical control. The majordesign details are captured by the semantics we present in this paper, while the external functionscan be implemented by the user if they want to do so. In applications written in PCCL, agentscommunicate using shared variables. Shared variables in practice are implemented throughmessage passing on hardware platforms [8]. In this paper, we present a semantics which has aneventual consistency, but our design is modular enough to implement different consistency
models. In our semantics, the external functions which control interaction with the physicalenvironment are parameters provided to the semantics. Several other application specific featurescan also be provided as external functions, such as communication restrictions based ongeographical proximity. We assume that all agents can communicate with all other agents. InSection 5, we discuss our planned implementation of a publish-subscribe model ofcommunication among agents.

We use the K semantic framework to write the semantics of this language, as it can be used to generate executable semantics which lets us run applications and generate execution traces. We talk about K in Section 3. We also discuss a distributed system implemented using this language.

1.1. Related Work

In this work, we have introduced the conventional semantics of a language for circulated specialist coordination and control. The principal focal point of this work was on fostering a proper model for nonconcurrent simultaneous applications where correspondence happens through shared memory. P is a language for nonconcurrent occasion driven programming, which permits the developer to determine the framework as an assortment of cooperating state machines, which speak with one another involving occasions rather than shared memory refreshes as in PCCL. In a genuine execution (like StarL), specialists really do answer message occasions, which could on a basic level be displayed in P. Our work gives a structure that permits a somewhat beginner client to compose pseudocode without being worried about execution subtleties, similar to dialects like Esterel [9], Radiance [10] and Signal [11]. As in our model of time development, these dialects likewise follow a model where time progresses in advances.Nonetheless, since we express our semantics in the K system, we can investigate differentinterleaving semantics. In these dialects, given a state and a contribution at the ongoing time step, there is an extraordinary conceivable state at the following time step. In any case, in an operating system or a circulated framework, it is difficult to have every one of the parts of the frameworktimed utilizing a world-clock, and thus nonconcurrent models are utilized for these frameworks,which gives a language like P a benefit over PCCL. In such models occasions are lined, andconsequently can be deferred randomly prior to being taken care of. Hypothetically, we canlikewise display postpones like this by upholding use of explicit revise-manages over and over,however that would restrict the consensus of the semantics.

2.LANGUAGE AND SYSTEM OVERVIEW

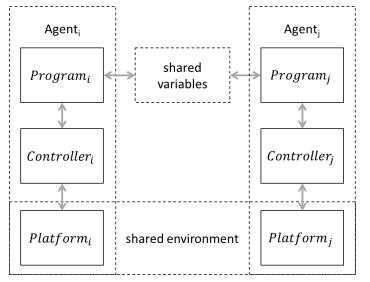
In this section, we give an overview of the system architecture within which PCCL programs execute and then discuss key language features with an example. We call an entity executing a PCCL program an agent or a process. The hardware abstraction on which PCCL programs execute includes (a) a controller, (b) shared memory, in addition to the usual (c) local memory and processing unit of the agent. The controller receives lists of way-points and obstacles from the agent’s program, drives the actuators (e.g. motors) to reach the way-points while avoiding the obstacles using sensors (e.g. GPS), and updates certain flags to indicate its status to the program The shared memory abstraction provides single-writer and multi-writer distributed sharedvariables using which an agent’s program can communicate with another agent’s program.

For this paper, we assume that all agents execute the same PCCL program; each agent knows the IDs of all participants; and there is a common coordinate system for the physical space within which the agents are operating. A program is a collection of variable declarations and events. The language provides two types of shared variables: (a) a multi-writer shared variable x is declared as allwrite and allows all agents to do reads and writes on x. (b) a single-writer shared variable x is declared as allread, and it creates an array x⟨·⟩ where the i’th component x⟨i⟩ can be read by all but can only be written to by agent i.

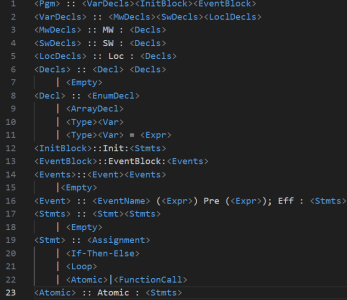
A PCCL program is organized as a collection of events. Each event nominally has a precondition (or guard) and an effect. The effect is a sequence of program statements and it may be executed only when the precondition holds. An event is said to be enabled if its precondition holds. If multiple events of a given agent program are enabled, then any one of them is chosen. There is a special event called Init that is executed when the program starts. Fig 1. Shows the syntactical structure of the language.

MW refers to middleware declarations, usually consisting of shared global variables used for global state management, inter-agent communication or other shared resources. These are synchronized across agents. Eg: Task Queue, shared lock, common memory buffer.

SW refers to software declarations managed with an agent’s application layer and are used to maintain agent-specific state or manage local computations. Eg: Status Flags.

Loc refers to local declarations managed within an event block, used temporarily during the execution of that block. Eg: loop counter, temp buffers, intermediate computation results.

Each of the above declarations follow a recursive structure Decls made of a composite pattern. It can have a single declaration or a group of declarations. A single declaration can be an enum, array or a custom type.

Figure 1. Syntactical Structure of the Language

PCCL provides a special operation doReach for programs to interact with the agent’s controller (see Fig. 2). A call to doReach instructs the controller to move towards a target (position or configuration) while avoiding a set of obstacles— both specified in the common coordinate system. Successive calls to doReach may update the sequence of targets and obstacles. The controller communicates with the program using two flags: (a) doReach_done is set if a neighborhood of the target is reached, and (b) doReach_fail is set if the controller determined that it cannot reach the target while avoiding the obstacles. Implementations of controllers for different kinds of agents platforms (e.g., ground rovers and quadcopters) provide different besteffort strategies.

Figure 2. Agent programs interact through shared variables. Each agent program also sets waypoints for its own controller which control the physical motion of the agent’s platform. The agent platforms inhabit a shared physical environment, and therefore, also interact physically

2.1. An Illustrative Example

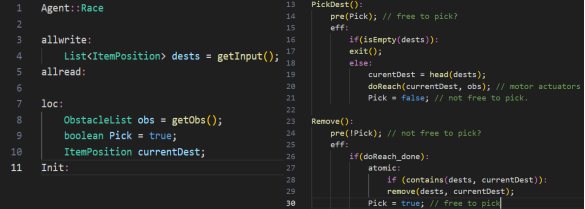
We present a simple illustrative example to demonstrate some of the features of the language, and to aid discussion in future sections. We want to design an application where (a group of) robots try to visit a predetermined sequence of waypoints, with predetermined obstacles, as shown in Fig 3. We aim to ensure that a robot choosing the next destination will not pick a waypoint that has already been visited by some robot, warranting a lock semantic.

The code for this application is provided in Figure 4. ItemPosition is a built-in datatype which is used to represent the position of the robot (the physical coordinates (x,y,z)). The robots have a shared list of ItemPositions (dests) which is initialized using the built-in function getInput. We define a boolean variable Pick which determines whether the robot is in the stage of picking and moving to the current destination currentDest or removing the current destination from the shared list of destinations, since it was visited. Functions such as getInput, getObs are provided asuninterpreted functions, which can be defined in an external language as long as they return values with consistent types.

The first stage is PickDest, when the next destination in the race is set, the robots try to reach it while avoiding the provided obstacles. Then in the Remove stage, each robot atomically updates the list of destinations to be visited if it reached the current destination. The atomic construct ensures mutual exclusion while updating a shared variable. The function remove can only remove an item from a list if it contains said item, the execution gets stuck otherwise. With that in mind, we added a check for whether the currentDest is contained in dests within the atomic block; toensure that between this check and atomically trying to remove the list element, another robot didn’t successfully already remove the same element.

Figure 3. A grid representing the physical environment with predetermined obstacles, agents and ItemPosition.

3. PCCL LANGUAGE SPECIFICATION

3.1. Syntax

This section describes the formal syntax of PCCL. We first provide the major features of the formal syntax which describe program structure, event structure, and statement structure. As mentioned in the overview in Section 2, each program consists of three major parts, with variable declarations, an initialization block and an event block. Aside from usual data types and arrays, we provide support for declaring enumerated types, as it is easy to use them as “stages” in applications.

Events, as mentioned earlier are specified by precondition-effect blocks, where the precondition is a boolean expression, and effect blocks contain statements, which can be assignment statements, if-then-else statements, atomic statements, function calls, or loops.

In this section we describe the formal semantics of key language elements. The system consists of N agents A1,…,AN. The state of the overall system advances by two types of transitions: (a) program transitions correspond to agent program events updating agent variables and possibly setting waypoints for the agent’s controllers. Program transitions take zero logical time. (b) environment transitions correspond to the physical environment of the agent evolving over an interval of time. During this period, the agent platforms may be moved by their controllers and messages implementing the distributed shared memory abstraction are propagated. Environment transitions are external to PCCL, and therefore, in providing executable semantics these transitions have to be implemented by external function(s). Thus, a given PCCL program may be executed with different external functions, to obtain different executions.

In the Race application of Section 2.1, for example, the state updates brought about by the PickDest and Remove events are program transitions and take zero logical time. In between these transitions, time may elapse and the corresponding change in the position of the agent is determined by its controller, its physical environment, etc., which are external to the program. Sample code snippet is seen in Fig 4.

Figure 4. Race Application

3.2. Overview of K

We give the semantics of PCCL abstraction utilizing the K framework [12], [13]. K is a changebased executable system for characterizing language semantics. Given a grammar and a semantics of a language, K produces a parser, a mediator, as well as investigation devices, for example, model checkers and insightful program verifiers “free of charge”.

For example, the state-space investigation ability troubleshoots PCCL programs. For demonstrating connections between specialists, an engaging part of K is its inborn help for nondeterminism. Reworking logic [14], [15], [16], makes K appropriate for thinking about circulated frameworks that are non-deterministic.

In K, a language sentence structure is characterized utilizing ordinary Backus-Naur Structure (BNF). The semantics is given as a progress framework, explicitly, as a bunch of decrease rules over designs. A configuration is a portrayal of the program code and state. For PCCL, a design addresses the code and the program state for all the specialist, as well as the condition of the actual climate (see Figure 1). Parts or individuals from a setup are called cells. The documentation ⟨celltype⟩cellname addresses a entity called cellname with a worth of type celltype. A unique cell, named k, contains a rundown of calculation to be executed. Cells might be nested, that is to say, contain different cells.

The level line portrays a rewrite from previous state (above) to result (below). Cells without a level line, for example, ⟨X → V⟩memory, are perused, yet not changed by the rewrite. The ellipsis (···) matches the segments of a cell that are neither perused nor composed by the standard. For example, the rule in Fig 5. is applied when the current computation is a look-up expression X; X is mapped to a value V in memory. The rule rewrites X to V.

Figure 5. Rule Lookup

3.3. Agent Cells and System Configuration

Each agent has an agent cell (see Fig. 6A) which stores the program variables of the agent, its execution context, as well as environment variables that are relevant for the agent such as the agent’s position. The agent cell consists of the following sub-cells.

• k: agent’s own application code
• id: agent’s unique integer identifier
• memory: a map from agent’s program variables to addresses
• position: agent’s current position in space in common coordinates
• counter: counts the number of times the agent’s event block has executed
• lockState: Denotes whether or not the agent holds the requested lock

The memory cell maps all—local and shared—variable names to addresses (of type Int). That is, the agent’s memory actually has copies of the shared variables. The position cell is specific to agents programs that rely on positional sensors. Other cells for different sensors can be included as well.

The top-level system configuration cell is called system (see Fig. 6B); it consists of the following main cells:

• agents: contain N agent cells. ; lets fix N as the number of agents.
• gMemory: maps all shared variables to addresses in the memory
• MMap: a map from memory addresses to variable values
• time: global time elapsed
• counterMap: map of agent ids to their counter (Section 3.5) values
• lockQueue: maintains the order of lock requests
• transitionState: indicates whether or not environment transitions are being executed.

Figure 6. A) Agent Cell

Figure 6. B) System Cell

The next subsections describe the semantics of PCCL in terms of rewriting rules for system configurations using the K-Framework semantic model.

3.4. Local Variable Declaration

A statement:

local T x;

declares a local variable called x of type T. The following rewrite-rule (see Fig. 7) captures a local variable declaration. It creates (a) an entry in the memory cell, that maps the variable name x a free address in MMap and (b) an entry in the MMap cell, that maps the aforementioned address to an undefined value, and (c) the line of code with the declaration is rewritten to empty (·). Shared variable declarations are processed similarly, except, that a copy of the variable is stored both at the global memory gMemory and at each agent’s memory.

Figure 7. Variable Declaration Rule

3.5. Events and Time Advancements

Time in the system is broadly categorized into two parts – discrete and continuous.

Discrete Time N is local to an agent i and is tracked using counter and is globally shared in counterMap. Discrete time threshold n0 is a predefined limit on the counter value which determines the maximum discrete cycles an agent has to perform within a continuous time interval δ. Therefore, N is reset to 0 with every δ increment of continuous time T. The K-Form for a program transition is capture in Fig. 8 below.

Figure 8. Program Time Transition Rule (Discrete Transition)

Continuous Time T is the global time of the System as a whole and governs the synchronization of all agents with the shared variables. The time cell models real-time of the system and it advances when the environment transitions occur. The program transitions (events) take zero time. In general, PCCL programs can produce zeno behavior whereby arbitrarily many program transitions occur at the same real-time. The K formalization for PCCL enables us to control the executable semantics with the following two parameters:

• δ: time elapsed over a single environment transition
• n0: maximum number of instantaneous program transitions per agent.

The counter and counterMap cells in the system configuration ensure that each event block can execute at most n0 times, before an environment transition occurs.

Consider an event block ‘pre(C); eff : S Es’ where S is a list of statements, and Es is the list of events following the first event. If C holds then the first event rewrites to S, else it rewrites to Es. After an event occurs, the agent’s counter is incremented and if it is less than n0 then the event block starts executing from the top again.

The continuous-time transition advances global time from T to T + δ. The transitionState is set from discrete to continuous. The K-Form for continuous-time transition is captured in Fig. 9 below.

Figure 9. Continuous Time Transition Rule

3.6. CAP Theorem and Discrete-Time-Threshold

It is worthy to note that Discrete Time Threshold n0 effectively can be considered as a configuration setting for either the system as a whole or a sub-cluster of agents of the system to determine if the system or the sub-cluster should behave with high consistency or high availability, thereby highlighting the fact that the proposed framework theoretically stays true to the CAP Theorem. The consistency and latency of the system are inversely proportional to n0. Conversely, throughput and availability are directly proportional to n0. Considering n0 = 1 would mean that an agent has to execute an event only once before the system synchronizes all agents and increments T. Therefore, the system performs at a high rate of synchronization and significant latency can be expected in the system at the cost of availability. This choice essentially is determined by the nature of the problem the system is designed to solve. A system performing payment operations would aim to have a high consistency whereas one sorting packages in an e-commerce warehouse can live with a drop in consistency.

3.7. Conflict Resolution

Given that synchronization among all agents in the system is a function of continuous time transition T, conflicts need to be addressed especially when n0 is higher. Note that sharedvariable synchronization takes places in one of two ways

i) when discrete time counter of all agents are equal to n0
∀i ∈ {1,2,…,n}, Ni=n0 where ‘i’ is the i’th agent
ii) when there is a change in the external physical environment of the system

Therefore, it becomes important to identify the nature of the system considering the use-case of the system before determining one of two ways to deal with conflicts emerging out of i) or ii) above

Agent Priority System (n0 first design) – continuous time T advanced only when all agents reach N=n0. Environmental changes are queued and processed after time advancement. This design favours deterministic execution and is ideal for safety-critical systems. Environment Priority System (reactive design) – continuous time advances on environment change. Agent progress is discarded and counters are reset. This design favours real-time systems and agent actions are independent or loosely coupled (i.e. low to no need of synchronization)

Table 1. Comparison of n0-first design and reactive design

The next section talks about the doReach abstraction and the associated external function, which govern the environment transitions.

3.8. Transition Dynamics

We first present the semantic rules involving the doReach abstraction. The physical environment uses the doReach component to communicate with the application, which in turn uses flags doReach_done and doReach_fail to store the event control variables used by the application. In this case, position is such a variable. Recall that doReach takes two arguments, the target, and the obstacle. The exact format of the obstacle is irrelevant to the semantics, as it is implementation specific to the doReach external function. This function is invoked whenever time advances. The target and the obstacles are set to current position and empty initially, unless the application specifies otherwise.

a) doReach invoke transition: The transitionState cell of the system is set to continuous when all the counter values of all agents reach n0. Suppose that the last observed position was P, and the time it was observed at was T0, the target is T, and the obstacles are stored in O. Time increments by δ during an environment transition. These variables are also updated at the end of every round, but we omit those details. The K-rule to process a doReach statement in the application is given in Fig 10.

Figure 10. Invoke Transition Rule

b) doReach update transition: When a doReach statement is encountered in the program, the statement itself is rewritten to empty. After which, the doReach flags should be reset (doReach_done, doReach_fail are both set to false). The K-rule for the update transition is given in Fig 11.

Figure 11. Update Transition Rule

3.9. Locking
We provide global locks to implement mutual exclusion for the atomic construct. These locks have two major properties:

• At any time, at most one agent can hold a lock.
• An agent needs to request a lock at most once before being eventually granted the lock.

The first property ensures mutual exclusion and the second ensures that high frequency agents do not monopolize the lock. While defining the semantics it is easier for us to present the rules in terms of a single global lock on all allwrite shared variables [17].

Each agent has a cell called lockState, which can have one of three values.

• idle : agent is not requesting or holding the lock.
• request : agent has requested the lock but not holding it.
• lock : agent is currently holding the lock.

We maintain the lock queue or the order in which requests to the lock were made by agents, in the cell lockQueue. A lockrequest is granted on a first-in-first-out basis. An agent is not allowed to add itself to the lockQueue unless its lockState is idle. Once it becomes the first element of the queue, its lockstate becomes lock. Then it can execute its atomic block, and immediately afterwards remove itself from the lockqueue. If we do not enable counter increments while an agent is in the lockqueue, since the event block execution takes zero logical time, all locks would be essentially granted immediately. We provide the rewrite rules governing locking below, again, given a time model τ = (δ, n0)

a) Lock Request Transition: The lock request transition is enabled when an agent with id i encounters an atomic block containing statements Ss, when its lockstate is idle. Then, the agent adds a marker atomicEnd just after the atomic block, to ensure that the agent releases the lock after executing it. At the same time, the agent adds itself to the end of the lock queue. Fig 12 shows the K-form of the lock request transition.

Figure 12. Lock Request Transition Rule

b) Atomic Wait Transition: The counter increment should be enabled when the lockState is request and the agent id is not at the head of the lockQueue. Since rewrite rules in the semantics can fire whenever they are enabled, this might result in an agent just continually incrementing its counter, and never doing anything else; thus simulating a failed or crashed agent. Fig 13 represents the K-form of the atomic wait transition.

Figure 13. Atomic Wait Transition Rule iff i1 != i2 and N < n0

c) Atomic Execution Transition: The agent acquires the lock when it is the first element of the lockQueue and starts processing the statements inside the atomic block. The counter does not increase in this rewrite, because once the lock has been acquired, the agent can immediately execute the atomic block. Fig 14 represents the K-form of the atomic execution transition

Figure 14. Atomic Execution Transition Rule< n0

d) Lock Release Transition: Once the atomic block has been executed, the lock must be released, the agent must poll itself out and set its own lockState to idle. The rest of the event continues to execute. Recall that in the lock request transition, we added a terminal atomicEnd after the atomic block. We can now use that to identify where the atomic block ends. Fig 15 represents the Kform of the lock release transition.

Figure 15. Lock Release Transition Rule< n0

3.10. Result

Sticking with the example in Section 2.1, multiple simulations of the solution was conducted with the following constraints.

i) The number of obstacles and their positions are fixed and the same for all simulations
ii) The number of items and their positions are fixed and the same for all simulations.
iii) The number of agents and their positions are fixed and the same for all simulations.

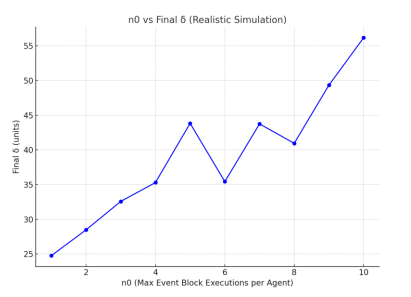
Therefore, the simulations only aim to establish a trend between n0 and T. For simplicity, we set δ=1. We enforce the above constraints because the relative position of the agents, the obstacles and the items will have an impact on T and therefore will not provide a true correlation between n0 and T. The aim of establishing the trend is to validate the hypothesis highlighted in Section 3.6 and the overall working of the framework proposed. With that in mind, the result is shown in Fig 16.

Figure 16. Correlation between n0 and total δ (or T, since δ = 1)< n0

The hypothesis in Section 3.6 holds good as we see that lower n0 results in faster completion of the task since agents do not wait for long for their peers to reach n0 and therefore, discrete time is smaller resulting in quicker continuous time ticks.

4. EXPERIMENTS

We perform two experiments, a positive test in section 4.1 and a negative test in section 4.2, to validate the correctness of the proposed atomic semantic in the framework

4.1. Fischer’s Protocol for Validating the Framework’s Atomic Semantic

Agents try to access a critical section mutually exclusively. Each agent is defined as follows. The agents have a shared variable called reqid which is used to request entry into the critical section. Another shared variable k is used to define wait times and entry times. Each agent initially waits for a time between 0 and k, (tracked by c1), and if the reqid is not set (reqid is −1), then it sets reqid atomically to its own id. Therefore, c1 is used to simulate two concurrent agents attempting to access the critical section. It then waits for d time (tracked by c2), and checks whether the reqid is its own id. If that is the case, then it enters the critical section, otherwise it goes back to waiting. If a robot enters the critical section, we make it spend cstime (tracked by c3 units of time) in the critical section to help detect mutual exclusion violations more easily. Since the passage of time should correspond to the increments of the variables c1, c2 and c3, we set n0 to 1, so that the continuous-time of the system increments every time the program time (discrete time N) of all agents increment. To ensure that this protocol works, the local in Cs variable of at most one agent can be true at time T. The assignment stage takes at least 2 increments of time, as we increment the counter every time an agent makes a lock request, and in this example, the time also increments as soon as the counter is incremented. The following execution trace shows that for d=2, we can violate this property. For bounded executions, we were unable to find traces which violated this property when d was set to a value greater than 2, which is expected. At time=0; both the agents have executed the Start event, indicated by the fact that the start variables of both agents, corresponding to addresses 8 and 22 respectively, map to false in the MMap. The waitTime for agent 0 is stored at address 7 and is seen from the MMap to be 6. The waitTime for agent 1 is seen to be 3. Refer MMap trace shown in Fig 17a.

At time=4, agent 1 is seen to be executing Assign event, as evidenced by the fact that variable assign for agent 1 stored at address 23 is true. Agent 0 is still waiting to start its Assign event, since its c1 is still 4 and its waitTime is 6. Refer MMap trace shown in Fig 17b.

At time=11, we see that the inCs values of both agents are true, which the protocol correctly detects owing to the waiting time d not being large enough to ensure coordination. During this execution, as agent 0 was assigning the reqid to its own id, agent 1 had entered the delay state. When the agent 1 checked whether it can enter the critical section, agent 0 hadn’t assigned reqid to its own id. Agent 1 set it’s inCs to true, which signifies that it is in the critical section, and still is in it when agent 0 enters after satisfying all requirements. Refer MMap trace shown in Fig 17c. This verifies that Fischer’s Protocol holds good when written and tested using the proposed framework

4.2. Race without Atomic Check

We revisit the race example from earlier, where a group of robots try to race to a predetermined set of points. In the PickDest state, the robots choose the next destination to race to. Then in the Remove stage, each robot atomically updates the list of destinations to be visited if it reached the current destination. Recall that we put the check for whether an element is present in the shared list dests inside the atomic block. We now perform experiments with two versions of doReachBB, the physical control black box, where the atomic block only contains the update, but not the membership checking.

The observed execution is that the agent cannot process the statement which asks to remove an ItemPosition from the dests, as between the time that it checked for membership and tried to update the list atomically, another agent already managed to remove the said ItemPosition. This is a negative test-case for validating the correctness of the atomic semantic proposed in the framework.

5. CONCLUSIONS

The paper successfully proposes a formal abstraction layer, a framework and a wrapper-language around PCCL and verifies the validity of the semantics adopted in the framework by using simulations and popular protocols. The use-case agnostic framework proposed here aims to provide a highly modular approach to writing application logic for multi-node distributed automation systems. These systems can range from robots on ground to drones or quadcopters in air and still onboard onto the framework owing to the abstraction details and interfaces highlighted earlier in the paper.

6. FUTURE WORK

We are currently extending the formal semantics of the language to include the implementation of neighborhood-based address information, and a publish subscribe model for shared memory.

We are developing PCCL to interface with the Stabilizing Robotics Language (StarL). StarL is primarily in Java, and it provides language constructs for coordination and control across robots. Two key features of StarL are a distributed shared memory (DSM) primitive for coordination and a reach-avoid primitive for control. DSM allows a program to declare program variables that are shared across multiple robots. This enables programs running on different robots to communicate by writing-to and reading from the shared variable.

All the program threads implementing the application, the message channels, as well as the physical environment of the application (robot chassis, obstacles) are modelled as hybrid automata, and the overall system is described by a giant composition of these automata.

We also plan to employ and extend the verification tools K provides; for instance, symbolic execution to verify the correctness of applications. We are currently only looking at invariants, and future work can involve exploring progress guarantees as well.

Figure 17. A) MMap at time=0 B) MMap at time=4 C) MMap at time=11

7. LIMITATIONS

The paper aims to provide a reusable, modular abstraction model and a sound framework to break down the development cycle for application logic of tedious and complex multi-node distributed systems in the field of robotics, automation and IoT. The paper does not provide insights into performance metrics or reliability metrics, as these vary from system to system based on the system design in question [17][18]. The abstraction layer however, can be applied on top of any backend system design, as the proposed framework.

CONFLICTS OF INTEREST

The author declares no conflicts of interest.

REFERENCES

[1] C. Steiner, “Bot in the delivery:kiva systems,” Forbes Magazine, March 2009, http://www.forbes.com/forbes/2009/0316/040_bot_time_ saves_nine.html.
[2] E. Asarin, O. Bournez, T. Dang, A. Pnueli, and O. Maler, “Effective synthesis of switching controllers for linear systems,” in Proceedings of IEEE, vol. 88, no. 7, July 2000, pp. 1011–1025.
[3] J. Misra, G. Morrisett, and N. Shankar, Eds., Workshop on The Verification Grand Challenge, SRI International, Menlo Park, CA, 2005.
[4] R. Goebel, R. G. Sanfelice, and A. R. Teel, Hybrid Dynamical Systems: Modelling, Stability, and Robustness. Princeton University Press, 2012.
[5] T. A. Henzinger, P. W. Kopke, A. Puri, and P. Varaiya, “What’s decidable about hybrid automata?” in ACM Symposium on Theory of Computing, 1995, pp. 373–382. [Online]. Available: citeseer.nj.nec. com/henzinger95whats.html
[6] T. Henzinger, “The theory of hybrid automata,” in Proceedings of the 11th Annual IEEE Symposium on Logic in Computer Science (LICS ’96), New Brunswick, New Jersey, 1996, pp. 278–292. [Online]. Available: citeseer.ist.psu.edu/henzinger96theory.html
[7] [7] T. Johnson, S. Mitra, and K. Manamcheri, “Safe and stabilizing dis tributed cellular flows,” in Proceedings of IEEE International Conference on Distributed Computing Systems (ICDCS 2010), 2010.
[8] A. Zimmerman and S. Mitra, “A programming environment for peer-to peer applications over ad hoc wifi and android phones,” 2012.
[9] H. Hermanns, J. Meyer-Kayser, and M. Siegle, “Multi-terminal binary decision diagrams to represent and analyse continuous-time markov chains,” in Workshop on the Num. Sol. of Markov Chains, 1999, pp. 188–207. [Online]. Available: citeseer.ist.psu.edu/hermanns99multi.html
[10] N. Halbwachs, P. Caspi, P. Raymond, and D. Pilaud, “The synchronous data flow programming language lustre,” Proceedings of the IEEE, vol. 79, no. 9, pp. 1305–1320, 1991.
[11] J. Elson, L. Girod, and D. Estrin, “Fine-grained network time synchronization using reference broadcasts,” 2002. [Online]. Available: citeseer.nj.nec.com/elson02finegrained.html
[12] R. Grosu, S. Mitra, P. Ye, E. Entcheva, I. V. Ramakrishnan, and S. A. Smolka, “Learning cyclelinear hybrid automata for excitable cells.” in HSCC, ser. LNCS, A. Bemporad, A. Bicchi, and G. C. Buttazzo, Eds., vol. 4416. Springer, 2007, pp. 245–258.
[13] R. Grosu, G. Batt, F. H. Fenton, J. Glimm, C. Le Guernic, S. A. Smolka, and E. Bartocci, “From cardiac cells to genetic regulatory networks,” in Computer Aided Verification. Springer, 2011, pp. 396–411.
[14] A. Bemporad, A. Bicchi, and G. C. Buttazzo, Eds., Hybrid Systems: Computation and Control, 10th International Workshop, HSCC 2007, Pisa, Italy, April 3-5, 2007, Proceedings, ser. LNCS, vol. 4416. Springer, 2007.
[15] A. Bemporad, A. Bichi, and G. Buttazzo, Eds., ser. LNCS, vol. 4416. Springer, 2007.
[16] A. Donzé and O. Maler, “Systematic simulation using sensitivity analysis,” in HSCC. Springer, 2007, pp. 174–189.
[17] V. Ramji, “Scalable Consensus for Blockchain Networks,” in Proceedings of the Computer Science & Information Technology Conference, vol. 14, no. 2, AIRCC Publishing Corporation, 2023, pp. 1–14. [Online]. Available: https://airccse.org/csit/V14N24.html.
[18] A. Thomas, NV. Eldhose, “Lorawan Scalability Analysis- Co-Spreading Factor Interference,” International Journal of Computer Networks & Communications (IJCNC), vol. 12, no. 5, AIRCC Publishing Corporation, [Online]. Available: https://ijcnc.com/2020/02/07/ijcnc-05-10/.
[19] M. D’Arienzo, M. Napolitano, SP. Romano, “Controller Placement Problem Resiliency Evaluation in SDN-Based Architectures,” International Journal of Computer Networks & Communications (IJCNC), vol. 14, no. 5, AIRCC Publishing Corporation, [Online]. Available: https://ijcnc.com/2022/10/15/ijcnc-07-22/.

AUTHORS

Vivek Ramji is a graduate with Master of Science degree in Computer Engineering from Dept. Electrical & Computer Engineering at Stony Brook University and a Senior Software Engineer at Microsoft with a keen interest in scalable and performant Distributed Systems.