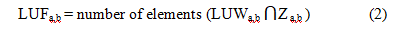IJCNC 02

Deadline-Aware Task Scheduling Strategy for Reducing Network Contention in NoC- Based Multicore Systems

Mohd Farooq ¹, Aasim Zafar ¹ and Abdus Samad ²

¹ Department of Computer Science, Aligarh Muslim University, Aligarh, India

² Department of Computer Engineering, Aligarh Muslim University, Aligarh, India

Abstract

Network on Chip (NoC) has revolutionized on-chip communication in multicore systems, establishing itself as a critical design paradigm for modern multicore processors and System-on-Chip (SoC) architectures. In contrast to standard bus-based interconnects, NoC employs a network-like structure that enables scalable and efficient communication between several processing components. This technique has addressed the issues raised by the rising complexity of integrated circuits, providing higher performance, reduced latency, and increased power efficiency. NoC has played a critical role in enabling the development of high-performance computing systems and sophisticated electrical devices by facilitating robust communication channels between components, marking a substantial shift from earlier interconnect technologies. Mapping tasks to the Network on Chip (NoC) is a critical challenge in multicore systems, as it can substantially impact throughput due to communication congestion. Poor mapping decisions can lead to an increase in total makespan, increase in task missing deadlines, and underutilization of cores. The proposed algorithm schedules tasks to cores while considering network congestion through various links and availability of processing elements. The experimental results demonstrate that the proposed algorithm improves task deadline satisfaction and minimize makespan by 23.83% and 22.83%, respectively, when compared to other dynamic task allocation algorithms.

Keywords

Dynamic Scheduling, Network on Chip, Makespan, Multicore, Deadline

1.   Introduction

Multicore systems integrate multiple processing elements (PEs), intellectual property (IP) cores, and memory units (MUs) onto a singular chip, establishing a high-performance computing platform. In multicore systems, the Network-on-Chip (NoC) functions as a communication framework due to its flexibility, reusability, scalability, and parallelism, surpassing the traditional communication method of bus-based architecture [1], [2]. The NoC communication architecture consists of network interfaces (NIs), routers, and links. Each core communicates with the router through a network interface, by converting data into a packet form. The routers are interconnected through on-chip links, forming the NoC topology [3][4]. The packetized transmission of data between two processing elements takes place as packets traverse routers, adhering to a routing policy, across the network links from source to destination cores. Multicore systems are an integral part of the rapid advancement of modern technology whether in High Performance Computing, Artificial Intelligence, or Cybersecurity [5], [6].

The main challenges faced in designing of multicore systems is to efficiently use the computational resources while utilizing less power as possible and find a suitable interconnect

architecture to connect the available cores to minimize any delay in data transmission. Therefore, application mapping is an important aspect of efficient utilization of multicore systems [7][8]. The tasks present in an application are mapped according to their dependencies on each other such that the communicating tasks are mapped to processing cores in vicinity. As the tasks are dependent on each other, when the execution of a task is completed, it sends data to all its dependent tasks. Multiple communicating tasks will be sending data through the interconnection network at the same time. Furthermore, when a network link is taken by a data packet from one communication traffic, another data packet requiring the same link needs to wait for some time until the link becomes free. This will lead to high latency or communication delay. For data- intensive applications high latency will adversely affect the execution efficiency of the system[9][10]. Therefore, it is highly required to jointly consider the computational load as well as the communications required for transferring data between different links in a given application.

Most existing work only considers application mapping to various cores and ignores the communication between various cores in an NoC [11][12]. In real time dynamic applications, tasks are submitted randomly to a multicore system. This means that the exact arrival time and the sequence in which they are arriving of tasks is not known[13][14][15]. In some cases, the execution time of tasks is also not known prior. For such type of applications, it is very important to map the tasks according to their communications to reduce the communication latency and decrease the execution time. All the decisions such as the start time of execution of a task, core assigned to a task, the time at which the communication will start are taken at runtime. On the other hand, static approaches are only applicable to a predefined set of tasks having fixed execution time. But static approaches are unaware of runtime resource variation and cannot be applied to scenarios having runtime task variation or data transfer through various links in a NoC [16][17]. Therefore, dynamic task allocation with contention awareness is a challenging task on multicore systems[18][19]. Along with computation it also considers the communication through various links in an NoC in case of dynamic scenarios. Most of the previous studies in this field either allocates the task dynamically and ignores the communication through NoC or focuses only on communication through NoC ignoring the computational part [20][21]. In this work, we propose an efficient solution for real-time dynamic task allocation and scheduling while considering the network contention. The proposed work allocates tasks to various cores dynamically and also considers the data transfer through various links in an NoC. This algorithm checks for network contention before each data transfer and chooses the alternate path or an alternate core in case of network contention. This algorithm reduces the network latency by reducing the conflicts between data transfers. It decreases the overall execution time due to changes in the method of selecting the route using the route utilization factor and also leads to a number of tasks satisfying the deadline. The salient features of the proposed work are:

• This paper proposes a dynamic scheduling algorithm for jointly allocating the tasks to various cores and scheduling the computational workload through various links and NoC-based multicore system.
• It provides an online method that takes into account the future traffic using the route utilization factor and dynamically chooses a route for data packets between the links.
• It proposes an improved heuristic method to dynamically allocate tasks leading to a reduction in overall execution time, improved deadline performance and reduced network latency.
• The proposed method ensures optimal task allocation and effective network utilization of the NoC architectures, making it a viable solution for real-time dynamic scheduling in multicore systems.

The remainder of this paper is organized as follows: the related work is discussed in Section 2. The system model considered for this work is explained in Section 3. The proposed dynamic algorithm is explained in Section 4. The experimental results obtained from the proposed algorithm are compared to other dynamic algorithms in Section 5. Finally, Section 6 presents the concluding remarks.

2. Related Work

A dynamic mapping algorithm Minimum Maximum Channel Load(MMCL) was proposed in [22]. This heuristic calculates the channel load for all possible mappings for any new task inserted in the system. Its main aim is to minimize channel usage which has a high value of channel load. Since MMCL considers all NoC channels before allocating a task. Another dynamic mapping heuristic Path Load (PL) was also proposed in [22]. This heuristic only considers only those link segments which will be used by the task under mapping. It chooses the path with a minimum value of Path Load. The path load algorithm only considers the traffic on the path but does not consider the load on the processing cores.

In Communication Aware Nearest Neighbor (CA-NN) [23], the parent task is mapped at the center of the cluster of processing elements. For all the unmapped tasks, a basic ordered list of processing elements is formed for every task. The basic ordered list is formed in a top, down, left right manner. The processing elements are searched in increasing order of hop counts. If a suitable processing element is not found in 1 hop count, it is searched at 2 hop count. If the selected task can be run on the processing element, then the previously mapped tasks on that processing element are found. Then it is checked whether any of the previously mapped tasks on the processing element is the parent of the selected task. If a selected task’s parent is found, it is mapped on the processing element. Otherwise, the next processing element is checked so that the current processing element can have the child task of the currently allocated tasks. If the selected task has no parent task, it is allocated at the first suitable processing element. Resources are updated after every mapping so that the other future tasks can have accurate information about the task’s mapping. CA-NN can be used in static as well as dynamic scenarios, In CA-NN a processing element can execute more than one task. It depends on the maximum capacity of the processing element. It is a communication-aware heuristic because it searches for communication with a parent task while allocating a new task to a processing element. CA-NN can execute more number of tasks than the processing cores. However, in this algorithm two tasks can send data through a link at the same time leading to network congestion. This algorithm also does not consider task deadlines leading to deadline violation.

Another dynamic task scheduling strategy was proposed in [24]. This method involves the implementation of a management unit employing the method of trellis search to identify the paths with reduced contention and lowering the communication latency between the source and destination tiles within a network-on-chip. It searches for a suitable tile in all directions simultaneously like flooding, resulting in faster searching speed as compared to previous similar methods. This method incorporates a hardware-based allocation manager to guarantee lower latency and enhance the mapping speed. However, this strategy introduces an additional overhead of hardware implementation.

In another similar approach the Smart Hill Climbing Algorithm[25], the authors employed a simplified algorithm to identify an appropriate location for a given application. The authors modified the process of selecting the initial processing core/node by incorporating the method of square factor. This square factor plays a crucial role in determining the number of adjacent nodes, forming nearly square shapes that surround the initial node. The dynamic task mapping strategy tries to choose a minimal mapping distance or identify a continuous region for traffic to reduce communication latency. In the context of real-time mapping scenarios, however, it becomes impractical to allocate all tasks using this algorithm.

A dynamic task mapping algorithm with congestion speculation (DTMCS) was proposed in [26]. This algorithm only executes an application if the number of tasks in an application is lesser than the number of number of tiles in a NoC architecture. Otherwise, it rejects an application. At the start, all tasks are placed in a ready queue using BFS. It starts by mapping the parent task to the first available tile. The initial execution occurs on the first tile with the parent task of an application. Subsequently, the child tasks of the executed parent task are selected sequentially for execution. The destination tile for each child task is determined using Manhattan Distance, starting from the lowest value. Once a suitable destination tile is found, the communication edge is assigned to the connecting links between the source and destination tiles. The Speculation Time Window (STW) is updated following each data transfer through a link. Speculation Time Window (STW) values serve as a means to avoid network contention. When a tile intends to transmit data via a link, the STW values of the link are compared with the current link usage. In the presence of network contention, the sending tile is required to wait for a specific duration determined by the intersection of STW values and the current link usage. Data is then transmitted through the route with minimal or zero route utilization. This entire process is applied to all traffic destined for the target tile. DTMCS is developed to be applied to dynamic scenarios only. This algorithm increases the idle time of cores because only a single task can be allocated to a processing core.

An improved throttle algorithm was proposed in [27]. This algorithm improved the throttle algorithm which was based on dynamic load balancing by maintaining a configuration table of available processing units and updating the list regularly after each task allocation. The disadvantage of this algorithm is that it needs to scan all the processing units before allocating a task and it leads to significant delays in task processing. It is also not effective if the processing units that are available for executing tasks are present at the bottom of that configuration table.

In [28], the authors introduced a Dynamic Task Scheduling Algorithm (DTSCA) for multicore systems where the issues of network contention and deadline satisfaction are both taken into account. This parent task of an application is allotted to the tile having maximum free neighbors. The child tasks of the task executed by the tile are then inserted in the ready queue. Then a child task is selected from the ready queue based on minimum slack time. After this, a suitable tile is chosen for the execution of the child task using the Manhattan Distance. Then it calculates the Link Utilization Factor (LUF) for all the links in the path between the source tile and destination tile. It then averages all values of LUF in the routs to get the Route Utilization Factor (RUF). It selects a tile if there is no link contention. Their approach checks for network contention for a link only once and then transmits the data at the next available cycle. Averaging all values of LUF to get RUF, leads to inaccurate wait time for a task. Therefore, the authors did not address the issue of network contention iteratively. This algorithm also waits for a higher amount of time at each network contention. If route is available then this algorithms does not check for the availability of the processing core, leading to an increase in waiting time for tasks.

In our previous work[29], we proposed an algorithm as an extension of the DTSCA algorithm which check the contention iteratively and improves the communication delay only. The algorithm parameters such as LUF and RUF were calculated according to the DTSCA algorithm. The other limitation of this work is that it was limited to quadcore systems only. In comparison to that, in this work, we proposed a new method to calculate the link utility factor, route utility factor, checked for network contention iteratively also added the feature of checking the availability of tile at any instant to reduce the average waiting time for tasks. This algorithm improves overall makespan, reduces the number of tasks missing deadlines as added featuresalong with minimizing network contention. This method is applied on multicore systems with varying the number of cores from 6X6 to 18X18.

3.   System Model

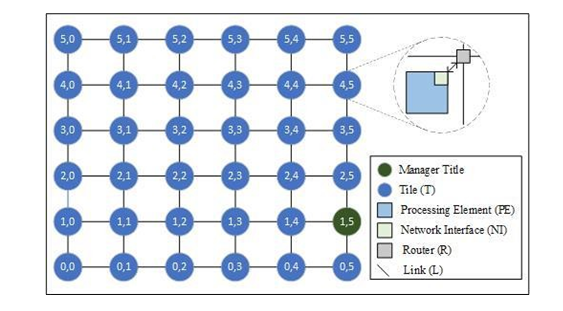
In our model, we considered a multicore system which is based on tiles. A multicore system consists of multiple tiles. Each tile contains a processing core, router, and network interface (NI). The processing cores are homogeneous in nature and the same architectural configuration. The communication architecture used to connect tiles is NoC. In this approach, we used 2D mesh NoC. Links are connections between tiles. Figure 1 shows the basic model of mesh NoC architecture.

Figure 1. Basic structure of a 6X6 NoC architecture

The tasks assigned to a tile are executed by the processing core. It is assumed that all the cores are homogeneous in nature. Data from the processing core is sent to the network via a network interface, where it is transformed into packet format and injected into the router. The router uses a routing algorithm to guide the data packets from the source to the destination. In the routing algorithm, two policies are employed to direct data packets. Initially, a route is determined using the XY routing policy. If the determined route is occupied, an alternative route is determined through the YX routing policy. If both routes are occupied, the transmitting router must delay the sending of data until one of the routes becomes free. Upon identifying a suitable route, packets are dispatched through the links connecting the source and destination tiles.

In our study, we considered a single manager tile responsible for hosting the operating system. We assumed that the OS supports non pre-emptive execution of tasks. This manager tile implements the scheduling algorithm and identifies the optimal tile for task execution. Incoming tasks in the system are mapped to the most suitable tiles by the managerial tile. The cores within each tile carry out task execution, transmitting the results to child tasks either within the same tile or across different tiles. All cores maintain complete control over executing the assigned tasks and transmitting the outcomes that generate at the end of task completion.

Application Task Graph: It is a directed acyclic graph (DAG) that comprises of a collection of tasks and edges. Each task is characterized by an execution time and a deadline, represented as ti(exei, dli). The edges in the graph are denoted by ei(ts, td, ew), where ts, td, and ew indicate the source tile, destination tile, and edge weight, respectively.

NoC Topology: The NoC topology comprises of an n*n network of tiles interconnected through various communication links. Every tile has an earliest available time, which is updated upon task completion on that tile. Routing policies establish a route R, where |R| indicates the length of a particular route, i.e., the total number of links present in a route. Contention is examined for each link at a specific time instant, and packets are transmitted once the communicating link becomes available. All the system model requirements are detailed in Table 1.

Table 1. System Model Requirements

The various terms used in the proposed algorithm are described below:

Link Utilization Window (LUW) for each link on the communication path is calculated using the formula provided in equation 1:

where,v represents the initiation time of communication, i.e. the instant at which the parent task has finished its execution.

ew represents the weight of the edge between the parent and child task

Link Utilization Factor (LUF) for each link in the path is calculated using the formula provided in equation 2:

where, Za,b signifies the time intervals during which a specific link (from tile a to tile b) is in use. Value of Z is updated at the start of data transmission when link is found to be free, so that the other tiles can check for contention.

Route Utilization Factor (RUF) for each link in the path is calculated using the formula provided in equation 3:

RUF gives the value of minimum amount of time to wait in case if the link is used by some other task for data transfer. If we take the average value of all the LUFs (LUF of all links in the path), this will give an inaccurate value of wait time which will ultimately leads to congestion.

4. The Proposed Algorithm

The proposed dynamic task allocation and scheduling strategy allocates tasks to various cores dynamically and then maps the various data transfers through different links by selecting a route dynamically to minimize network contention. Our proposed scheduling algorithm uses the best route in comparison to the previous DTSCA algorithm which reduces the overall latency. The tasks are dynamic in nature. The number of tasks is not fixed and can change at runtime. The arrival timings of tasks are also not known prior.

The proposed algorithm is given in two phases as described below: RLCAS

Input: Graph(tasks, edges), hop, mesh_size Output: Task to tile allocation and communicating edge allocation to links   task_scheduled = null; task_tile_allocation = null; 𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡 ← null; 𝐸𝑑𝑔𝑒_𝑙𝑖𝑠𝑡 ← null;

𝑡𝑟𝑜𝑜𝑡 = root task of 𝐺raph; 𝑡𝑙𝑟𝑜𝑜𝑡 = tile surrounded by the highest count of unoccupied neighboring tiles; assign tlroot to task troot; update task_tile_allocation; 𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡 ← child tasks of 𝑡𝑟𝑜𝑜𝑡; 𝐸𝑑𝑔𝑒_𝑙𝑖𝑠𝑡 ← Edges arriving at tasks in the 𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡; update Task_Tile_Allocation; while 𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡 OR 𝐸𝑑𝑔𝑒_𝑙𝑖𝑠𝑡 != NULL do 𝑡𝑠𝑒𝑙 = 𝑚𝑖𝑛_𝑑𝑙(𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡) ; 𝑡_parents = parents of 𝑡𝑠𝑒𝑙; t_children = children of 𝑡𝑠𝑒𝑙; t_parent = Check for multiple parents and choose the one which completed latest. for each t_child in t_children if (all parent tasks of t_child scheduled) 𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡 = [𝑅𝑒𝑎𝑑𝑦_𝑙𝑖𝑠𝑡, t_child]; end end   (𝑡𝑙𝑋𝑌, R𝑋𝑌, RUFXY, LUW) = 𝐷𝑅𝑆𝑇𝐶 (𝑡𝑙𝑝𝑎𝑟𝑒𝑛𝑡, 𝑡𝑠𝑒𝑙, 𝐸𝑠𝑒𝑙, ℎ𝑖𝑛𝑡, 𝑋𝑌 𝑅𝑜𝑢𝑡𝑒𝑃 𝑜𝑙𝑖𝑐𝑦); if (RUFXY == 0) then Update EATTl (𝑡𝑙𝑋𝑌); Update TaskTileAlloc; Update Z using LUW; else (𝑡𝑙𝑌𝑋, R𝑌X, RUFYX, LUW) = 𝐷𝑅𝑆𝑇𝐶 (𝑡𝑙𝑝𝑎𝑟𝑒𝑛𝑡, 𝑡𝑠𝑒𝑙, 𝐸𝑠𝑒𝑙, ℎ𝑖𝑛𝑡, 𝑋𝑌 𝑅𝑜𝑢𝑡𝑒𝑃 𝑜𝑙𝑖𝑐𝑦); If (RUFYX == 0) Update EATTl (𝑡𝑙𝑌𝑋); Update TaskTileAlloc; Update Z using LUW; else max1 = max (EATTl (𝑡𝑙𝑋𝑌), EAT(path)); max2 = max (EATTl (𝑡𝑙𝑋𝑌), EAT(path)); if (max1 <= max2) then Update EATTl (𝑡𝑙𝑋𝑌); Update TaskTileAlloc; Update Z using LUW; else Update EATTl (𝑡𝑙𝑋𝑌); Update TaskTileAlloc; Update Z using LUW; end end end update Readylist; update Edgelist; allocateroutes(send data to child tile from all other parents); endwhile

DSRTC Input: phi, tsel, edge_sel, tlparent, hop, routing policy, task graph, mesh Output: tlselected, best_route, updated_LOW_values, RUF, start_time all_tiles = all tiles having hop count less than hop from tlparent; Sort and shuffled tiles of same order in all_tiles;   for i = 1 to all_tiles tlselected = ith_tile; if (XYRoutingpolicy) Route_R = findroute (tlselected, tlparent, mesh, XYRoutePolicy); else Route_R = findroute (tlselected, tlparent, mesh, YXRoutePolicy); end for each link in R calculate LUW and then LUF; end RUF = maximum (All LUFs in route R); if (RUF = 0 && EAT(tlselected) = 0) return (tlselected, LOW, RUF, R); elseif (RUF = 0 && EAT(tlselected)! = 0) high_value = max (EAT(tlselected), max(LOW)); start_time = high_value; update (tlselected, LUW, RUF); else update the LUW values according to contention details; update modified LUW values; update start_time; update (tlselected, LUW, RUF, start_time); end endfor return(tlselected, LUW, RUF, start_time, R);

 

Where,

EAT = Earliest Available time.

EATTl = Earliest Available time of tile. tlselected = Tile Selected.

tlparent = Tile on which parent task is executed.

The first phase is defined as RLCAS. In this phase, the main inputs given are the task graph, hop size and the mesh size. The output it gives are allocating of task to various tiles and data transfer through various links. At the start of the algorithm there is an initialization phase. In this phase three list are defined the Ready_List, Edge_List and Task_Tile_Allocation list. The Ready_List and Edge_List are updated after every iteration of while loop. All the task whose parents have completed execution are added to Ready_List after the completion of each iteration. All the communicating edges are added to Edge_List after the addition of task to Ready_List. Task_Tile_Allocation list contains the various tasks which have completed execution and the tiles assigned to them.

In the first algorithm (RLCAS) root task of the task graph of an application is assigned to the tile having maximum free tiles in the vicinity. Here allocation of task to the tile indicates allocating the task to the processing core of a tile. Then the Ready_List is updated with all the tasks which are the child tasks of the executed task and only those tasks are added in the Ready_List whose all parent tasks are executed. If a task has more than one parent task, then it will only be inserted in the Ready_List after the execution of all the parents. The Edge_List is updated with all the communicating edges to the tasks which are present in the Ready_List. The Task_Tile_Allocation list is updated with the root task and the root tile.

After this the while loop starts execution and it executes till either the Ready_List or the Edge_List becomes empty. If one of the list becomes empty, it just allocates the remaining tasks or the remaining edges to the available tiles or links. In the loop, the first step is to select a task for execution. A task tsel is selected from the Ready_List for execution having the closest deadline. Next step is to search for the best parent task for the task selected. It is selected on the basis of communicating edges. The parent task having the most amount of communication with the Tsel is selected as parent task out of all the parent tasks available. The selected task tsel is executed on the tile which is closest to tile executing the parent tile for minimum delay in the network communication. Then the DSRTC function is called for finding a suitable tile for the selected task tsel using the XY routing policy. If RUF of the route comes out to be zero and the tile is available for execution, then it is executed on the tile given by DSRTC function and all the value like Z, EAT(Tl), Task_Tile_Allocation are updated accordingly. Otherwise an alternate tile is searched using YX routing policy. If the value of RUF is 0 in this case, then the alternate tile is selected for execution and value are updated accordingly. If RUF is not 0 for any tile in given hop count, it selects the tile with the min start time for execution using both routing policies. After selecting a tile, it updates Z values using LUW values, EAT(Tl), and Task_Tile_Allocation accordingly. Then at the last the Ready_List, Edge_List are updated with new tasks whose all parents have got executed and the corresponding edges. Allocate routes function is used to update all the incoming edges to the selected task tsel other than the parent one.

In the second phase, DSRTC function is given. This function is called from RLCAS function to get the best tile for implementing a task. It takes input all the basic requirements as input such as hop count, routing policy, tlparent, edge, phi, etc. The output it gives are best tile for child task, RUF, LUF, Route_R, start_time for the selected task.

This function starts by sorting the tiles in increasing order of hop count from the parent tile. If many tiles have same hop count it shuffles them between each other so they get picked randomly. Then it picks a tile from the sorted list starting with the lowest hop count. The next step is to find a route R using the given routing policy. Then for each link in the route R, it calculates the Link Utilization Window (LUW). LUW values are used to calculate Link Utilization Factor (LUF) for each link in the route. Using LUW values, we get the Route Utilization Factor (RUF). In our work, we took the maximum value of the LUF values of all links in the route. We took the maximum value of all the LUF because it gives the maximum contention in the link. If waited for this amount of time and checked again, the link might be available.

After this if the value of RUF comes out to be zero for any link and tile is also available then the selected tile is used for execution of current task. Otherwise, if RUF is zero and earliest available time of tile is less than the current time, then also the current tile is selected for execution. Otherwise if RUF is not zero and there is a contention in the link then the LUW values of link is updated according to the amount of contention and its LUF values are updated accordingly. It updates a new start time for the task which does not contain link congestion. Or if the EAT of tile is more than the present time only the start time is updated accordingly and is sent back to the calling function. Then at last, it returns all the parameters required by RLCAS function.

5. Results and Discussion

This section presents the outcomes derived from assessing the effectiveness of the proposed contention-based dynamic task mapping and scheduling approach. In this section, we evaluated the performance of the proposed algorithm. The results of the proposed algorithm are compared with the recently developed DTSCA algorithm and standard CA-NN algorithm. To evaluate the performance of the suggested scheduler, we conducted simulations using MATLAB on a multicore system with an Hp Omen Ryzen 5 4600H processor. Task graphs are random and are obtained from the standard tool TGFF [30]. The simulation parameters used in the experiment along with their corresponding values/ranges are given in Table 2. To ensure the reliability of our results and minimize potential biases, we have carefully designed our data collection approach. The task graphs used in our experiments were generated using TGFF, a widely accepted benchmark tool for the task graph generation. Additionally, we conducted multiple trials across different NoC configurations to validate consistency in results.

We adopted a systematic approach to data collection. Our experiments involved allocating different application task graphs to different NoC architectures, ensuring a diverse range of test scenarios. Specifically, we allocated 10 different applications, each containing 60 tasks, to NoC architectures ranging from 6×6 to 18×18 to analyze deadline performance and makespan. At last, we averaged the results obtained from all iterations to get our result. In a single iteration, we have applied the same task graph to all architectures to get results, this removes any form of bias. Additionally, we conducted a separate experiment with 20 applications, each containing 30 tasks, to assess scalability. Therefore, our approach remains robust and reliable within an acceptable tolerance level, providing meaningful insights into the impact of dynamic scheduling strategies on NoC-based multicore systems.

The results obtained are compared with the latest DTSCA algorithm and the standard CA-NN algorithm on the parameters deadline performance, total makespan and scalability of the proposed algorithm.

Table 2. Simulation parameters used for experiment and their values

5.1. Deadline Performance

In this subsection, results of deadline performance of the proposed algorithm are compared with the other two dynamic strategies CA-NN and DTSCA. In this experiment, we also allocated 10 different applications containing 60 tasks to the varying NoC architectures. We varied the NoC size from 6X6 to 18X18. The results obtained after comparison are shown in Figure 2. We observed that the percentage of tasks meeting deadline increases by 10.84% and 36.82% as compared to DTSCA and CA-NN algorithms. The increase in deadline performance is due to reduced network contention which will lead to more delay in execution of tasks. As latency while transferring of data decreases, therefore the proposed algorithm performs better than other two dynamic strategies in case of deadline performance. On the other hand CA-NN approach attempts

to allocate tiles to task by using the communication data between tasks but this approach results in link congestion when data from two tasks are sent through the same link. CA-NN approach does not checks for availability of route while transferring data which will lead to network congestion. Therefore the proposed dynamic strategy leads to more tasks meeting the deadlines as compared to other two strategies.

It can also be seen that numbers of tasks meeting the deadline increase as we increase the size of NoC architecture. This is because more free tiles are available to execute tasks leading to less delay in execution of tasks.

Figure 2. Comparison of deadline performance with varying Platform Size

5.2.  Total Makespan

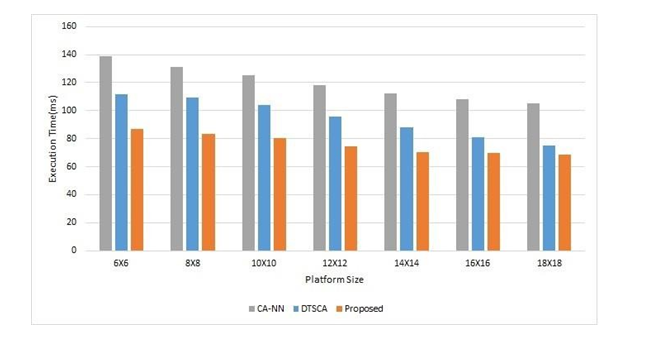
In this subsection, the results of the makespan of the proposed algorithm are evaluated. The results of the proposed algorithm are compared with the recently developed the DTSCA algorithm and the standard CA-NN algorithm. In our experimental setup, we varied the platform size from 6X6 to 18X18. We allocated 10 different applications each containing 60 tasks to all platform sizes and obtained the results of makespan. The results obtained are depicted in Figure 3. On an average, the proposed algorithm performs 15.65% faster than DTSCA algorithm and 36.43% faster than the standard CA-NN algorithm. While allocating a tile to a task, the proposed algorithm also checks for availability of the tile if the route is available. The proposed method checks for earliest available time of the tile and finds an alternate tile in case if the child tile is not available. While DTSCA allocate the task to a tile if the route utility factor comes out to be zero. It does not checks for the availability of destination tile. If the tile is busy this will lead to increase in waiting time for that task. This will lead to increase in overall makespan. The algorithm proposed in this study takes into account the timing characteristics of tasks and the utilization of their corresponding links. It aims to select an appropriate tile in close proximity to the parent task. This algorithm also uses a better estimate of route utility factor in comparison to other dynamic algorithms, so this also leads to less congestion in links, which ultimately leads to lower makespan. These considerations collectively contribute to minimizing the completion time of the mapped task, allowing for low-delay scheduling of subsequent child tasks. Consequently, the proposed method significantly reduces the makespan of allocated applications when compared to other two dynamic strategies.

Figure 3. Comparison of Execution Time with varying Platform Size

5.3.  Scalability of the Proposed Approach

This section presents the results of the scalability of the proposed approach with an increase in size of NoC architecture. We allocated 20 different applications with 30 tasks each to different NoC architectures. We used the timeit() function in Matlab to get the time taken by the algorithm to allocate all the tasks to tiles. The total time taken by 20 applications for scheduling the tasks is then divided by a total number of applications to get the average time for allocating an application. The results obtained are normalized with respect to the CA-NN algorithm at that architecture and it serves as a baseline for comparison. The results obtained are shown in Figure 4. The results on an average shows increase in 11.45% and 34.21% increase in timing overhead as compared to CA-NN and DTSCA algorithms. The results show an increase in timing overhead with increase in size of NoC architecture. The proposed algorithm show an increase in timing overhead due to increase in the number of tiles for higher NoC architectures. As it checks for extra links for link contention and it also checks for availability of tile, hence, the timing overhead increases. But it can be seen from the results, the proposed algorithm only shows a 25.26% increase in timing overhead as the number of tiles varies from 6X6 to 18X18, which is considerably low as compared to the increase in the number of tiles from 36 to 324(9 times).

Figure 4. Comparison of Execution Time with varying Platform Size

6.  Conclusion

In this study, we proposed an enhanced methodology for dynamic task allocation and scheduling in NoC-based multicore systems with contention-awareness. Our proposed algorithm takes into account the link utilization of the target multicore platform when determining the appropriate processing core for task execution. It calculates the route utility factor in an efficient way to further reduce link congestion. In real-time applications, it dynamically chooses a route to alleviate network contention during the data transfer from one tile to another. It also checks for the availability of tiles to reduce the overall makespan. To assess the effectiveness of our runtime algorithm, we conducted a comparative analysis with other dynamic task and communication mapping and scheduling algorithms found in the literature. The results obtained highlight the efficacy of our approach in terms of meeting deadlines and minimizing the makespan for the scheduled applications. The proposed method increases the number of tasks meeting the deadline by approximately 23.83%. It also reduces the overall makespan by 22.83%. It is also scalable as the total runtime of the algorithm only increases by 25.26% when the NoC architecture changes from 6X6 to 18X18. Therefore, this strategy results in better deadline performance and reduced makespan leading to improved performance in NoC based multicore systems. This strategy is also well-suited for the simultaneous allocation and scheduling of computation and communication workloads for NoC-based multicore systems.

Conflicts of Interest: The authors declare no conflict of interest.

References

1. K. Singh, P. Dziurzanski, H. R. Mendis, and L. S. Indrusiak, “A survey and comparative study of hard and soft real-time dynamic resource allocation strategies for multi-/many-core systems,” ACM Comput. Surv., vol. 50, no. 2, 2017, doi: 10.1145/3057267.
2. Teubler, D. Pfisterer, and H. Hellbrück, “Memory efficient forwarding information base for content-centric networking,” Int. J. Comput. Networks Commun., vol. 9, no. 3, pp. 67–85, 2017, doi: 10.5121/ijcnc.2017.9305.
3. Chen, C. Li, and P. Gillard, “Network-on-Chip (NoC) Topologies and Performance: A Review,”Proc. 2011 Newfoundl. Electr. Comput. Eng. Conf., pp. 1–6, 2011.
4. Joshi and M. K. Thakur, “Performance evaluation of various on-chip topologies,” J. Theor. Appl. Inf. Technol., vol. 96, no. 15, pp. 4883–4893, 2018.
5. Luqman and A. R. Faridi, “Authentication of fog-assisted IoT networks using Advanced Encryption credibility approach with modified Diffie–Hellman encryption,” Concurr. Comput. Pract. Exp., vol. 35, no. 22, p. e7742, 2023, doi: https://doi.org/10.1002/cpe.7742.
6. Alam Ansari and A. Zafar, “A fusion of dolphin swarm optimization and improved sine cosine algorithm for automatic detection and classification of objects from surveillance videos,” Measurement, vol. 192, p. 110921, 2022, doi: https://doi.org/10.1016/j.measurement.2022.110921.
7. Marculescu, U. Y. Ogras, L. S. Peh, N. E. Jerger, and Y. Hoskote, “Outstanding research problems in NoC design: System, microarchitecture, and circuit perspectives,” IEEE Trans. Comput. Des. Integr. Circuits Syst., vol. 28, no. 1, pp. 3–21, 2009, doi: 10.1109/TCAD.2008.2010691.
8. Z. Tei, Y. W. Hau, N. Shaikh-Husin, and M. N. Marsono, “Network Partitioning Domain Knowledge Multiobjective Application Mapping for Large-Scale Network-on-Chip,” Appl. Comput. Intell. Soft Comput., vol. 2014, pp. 1–10, 2014, doi: 10.1155/2014/867612.
9. Sheikh and A. Nagaraju, “Dynamic task scheduling with advance reservation of resources to minimize turnaround time for computational grid,” Int. J. Inf. Technol., vol. 12, no. 2, pp. 625–633, 2020, doi: 10.1007/s41870-020-00448-2.
10. K. Singh, J. Wu, A. Kumar, and T. Srikanthan, “Run-time mapping of multiple communicating tasks on MPSoC platforms,” Procedia Comput. Sci, vol. 1, no. 1, pp. 1019–1026, doi: 10.1016/j.procs.2010.04.113.
11. Chatterjee, S. Paul, P. Mukherjee, and S. Chattopadhyay, “Deadline and energy aware dynamic task mapping and scheduling for Network-on-Chip based multi-core platform,” J. Syst. Archit., vol. 74, pp. 61–77, Mar. 2017, doi: 10.1016/j.sysarc.2017.01.008.
12. T. Yuan, T. Huang, C. Xu, and J. Li, “A new approach to stochastic scheduling in Data Center Networks,” Int. J. Comput. Networks Commun., vol. 10, no. 5, pp. 1–25, 2018, doi: 10.5121/ijcnc.2018.10501.
13. Il Kim and J. K. Kim, “A Method to Construct Task Scheduling Algorithms for Heterogeneous Multi-Core Systems,” IEEE Access, vol. 7, pp. 142640–142651, 2019, doi: 10.1109/ACCESS.2019.2944238.
14. Baital and A. Chakrabarti, “Dynamic Scheduling of Real-Time Tasks in Heterogeneous Multicore Systems,” IEEE Embed. Syst. Lett., vol. 11, no. 1, pp. 29–32, 2019, doi: 10.1109/LES.2018.2846666.
15. Gaffour, M. K. Benhaoua, S. Dey, A. K. Singh, and A. E. H. Benyamina, “Dynamic clustering approach for run-time applications mapping on NoC-based multi/many-core systems,” 2020 2nd Int. Conf. Embed. Distrib. Syst. EDiS 2020, pp. 15–20, 2020, doi: 10.1109/EDiS49545.2020.9296439.
16. D. R. S. De Silva, N. Nedjah, and L. M. E. De Mourelle, “Static routing for applications mapped on NoC platform using ant colony algorithms,” Int. J. High Perform. Syst. Archit., vol. 4, no. 1, pp. 57–64, 2012, doi: 10.1504/IJHPSA.2012.047579.
17. Yao, P. Geng, and X. Du, “A task scheduling algorithm for multi-core processors,” Parallel Distrib. Comput. Appl. Technol. PDCAT Proc., no. September 2014, pp. 259–264, 2014, doi: 10.1109/PDCAT.2013.47.
18. Venugopal and T. G. Basavaraju, “Congestion and Energy Aware Multipath Load Balancing Routing for Llns,” Int. J. Comput. Networks Commun., vol. 15, no. 3, pp. 71–92, 2023, doi: 10.5121/ijcnc.2023.15305.
19. Pholpol and T. Sanguankotchakorn, “Traffic congestion prediction using deep reinforcement learning in vehicular ad-hoc networks (VANETS),” Int. J. Comput. Networks Commun., vol. 13, no. 4, pp. 1–19, 2021, doi: 10.5121/ijcnc.2021.13401.
20. Amin et al., “Performance Evaluation of Application Mapping Approaches for Network-on- Chip Designs,” IEEE Access, vol. 8, pp. 63607–63631, 2020.
21. Amin et al., “Performance Evaluation of Application Mapping Approaches for Network-on- Chip Designs,” IEEE Access, vol. 8, pp. 63607–63631, 2020, doi: 10.1109/ACCESS.2020.2982675.
22. L. D. S. Carvalho, N. L. V. Calazans, and F. G. Moraes, “Dynamic task mapping for MPSoCs,”IEEE Des. Test Comput., vol. 27, no. 5, pp. 26–35, 2010, doi: 10.1109/MDT.2010.106.
23. Carvalho and F. Moraes, “Congestion-aware task mapping in heterogeneous MPSoCs,” 2008 Int. Symp. Syst. Proceedings, SOC 2008, 2008, doi: 10.1109/ISSOC.2008.4694878.
24. Chen, E. Matus, S. Moriam, and G. P. Fettweis, “High Performance Dynamic Resource Allocation for Guaranteed Service in Network-on-Chips,” IEEE Trans. Emerg. Top. Comput., vol. 8, no. 2, pp. 503–516, 2020, doi: 10.1109/TETC.2017.2765825.
25. Fattah, M. Daneshtalab, P. Liljeberg, and J. Plosila, “Smart hill climbing for agile dynamic mapping in many- Core systems,” Proc. – Des. Autom. Conf., 2013, doi: 10.1145/2463209.2488782.
26. L. Chao, S. Y. Tung, and P. A. Hsiung, “Dynamic task mapping with congestion speculation for reconfigurable network-on-chip,” ACM Trans. Reconfigurable Technol. Syst., vol. 10, no. 1, 2016, doi: 10.1145/2892633.
27. N. Le and H. C. Tran, “Ita: the Improved Throttled Algorithm of Load Balancing on Cloud Computing,” Int. J. Comput. Networks Commun., vol. 14, no. 1, pp. 25–39, 2022, doi: 10.5121/ijcnc.2022.14102.
28. Paul, N. Chatterjee, and P. Ghosal, “Dynamic task allocation and scheduling with contention- awareness for Network-on-Chip based multicore systems,” J. Syst. Arch., vol. 115, doi: 10.1016/j.sysarc.2021.102020.
29. Farooq, A. Zafar, and A. Samad, “Contention-free dynamic task scheduling approach for network-on-chip based quad-core systems,” Int. J. Inf. Technol., Oct. 2023, doi: 10.1007/s41870- 023-01542-x.
30. P. Dick, D. L. Rhodes, and W. Wolf, “TGFF: task graphs for free,” in Proceedings of the Sixth International Workshop on Hardware/Software Codesign. (CODES/CASHE’98), pp. 97–101, doi: 10.1109/HSC.1998.666245.

Authors

Mohd Farooq is a research scholar in the Department of Computer Science at Aligarh Muslim University, Aligarh, India. He completed his master’s degree (MCA) from Aligarh Muslim University in 2017. His research areas include Parallel and Distributed Systems, Multicore Processors, and NoC Systems. He has contributed to and attended various national and international conferences.

Dr. Aasim Zafar is a Professor in the Department of Computer Science at Aligarh Muslim University, India. He has contributed extensively to national and international conferences and has published research in renowned journals. His academic interests and research areas encompass Mobile Ad Hoc and Sensor Networks, Software Engineering, Information Retrieval, E-Systems, Cybersecurity, Virtual Learning Environments, Neuro-Fuzzy Systems, Soft Computing, Knowledge Management Systems, Network-on-Chip (NoC) architectures, and Web Mining.

Dr. Abdus Samad is an Associate Professor in Department of Computer Engineering, ZHCET, at Aligarh Muslim University, India. His research interests include Parallel and Distributed Systems, Algorithm Design, Microprocessor Design, and Parallel System Design. With over 22 years of teaching experience, he continues to contribute significantly to his field.