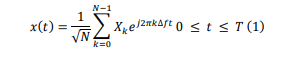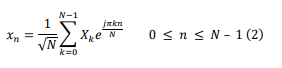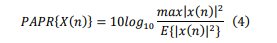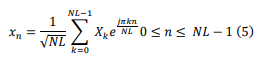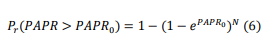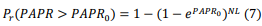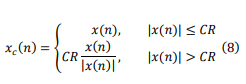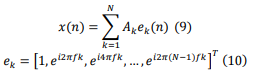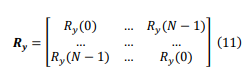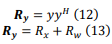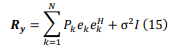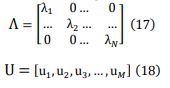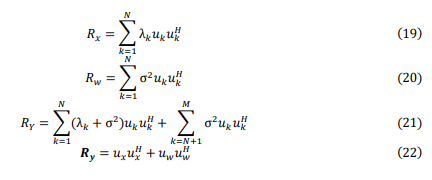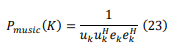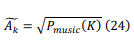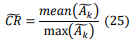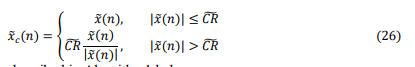IJCNC 04

ENHANCED PAPR REDUCTION IN OFDMSYSTEMS USING ADAPTIVE CLIPPING WITHDYNAMIC THRESHOLDS

Fatma Ben Salah 1, Abdelhakim Khlifi 2, Marwa Rjili 1, Amina Darghouthi 1 and Belgacem Chibani 1

1 MACS Laboratory, University of Gabes,Tunisia 2 Innov’COM laboratory, Sup’COM, University of Carthage, Tunisia

ABSTRACT

Orthogonal Frequency Division Multiplexing (OFDM) is a highly efficient multicarrier modulation method that is widely used in current high-speed wireless communication systems. It offers numerous benefits, including high capacity and resilience to multipath fading channels, when compared to other techniques. However, a significant drawback of OFDM is its high peak-to-average power ratio (PAPR), which can result in in-band distortion and out-of-band radiation due to the non-linearity of high power amplifiers. To address this issue, several techniques have been suggested, such as Selective Mapping (SLM), Partial Transmit Sequence (PTS), Clipping, and Nonlinear Compounding, which will be discussed later in the paper. The clipping technique, in particular, has been thoroughly analyzed as a simple and crucial method for reducing PAPR. However, an arbitrary choice of clipping threshold can result in significant signal distortion, degrading the transmission quality. Therefore, it is essential to find an optimum threshold that minimizes PAPR while preserving signal quality, which is a challenging task. The classical clipping scheme may not yield satisfactory results in this regard. This paper proposes a modified clipping scheme that estimates the dynamic range of a noisy OFDM signal. The estimated parameters are then used to determine the optimal threshold, which is more reliable than the previous technique that assumes an arbitrary dynamic value. Simulation results indicate that the proposed modified clipping scheme has achieved a PAPR reduction of 3.5 dB compared to the original OFDM.

KEYWORDS

OFDM; PAPR; Clipping; Threshold; Estimation; MUSIC; Eigen Decomposition

1. INTRODUCTION

The OFDM technology is a fundamental component of communication systems, offering numerous advantages over other methods [1]. These benefits include the ability to achieve high data rates, immunity to frequency selective fading and impulse interference, and tolerance of multipath delay propagation. Additionally, OFDM technology provides high spectral power efficiency, smooth equalization, and flexibility in hardware implementation [2,3,6]. Compared to other multicarrier techniques, OFDM is known for efficient bandwidth utilization [1,2,11], reduced susceptibility to echoes, and minimal non-linear distortion. These advantages have led to the widespread adoption of OFDM in various wireless communication systems, such as BRAN, WLAN, WiMAX, ETSI, LTE, DSL, and ADSL [2][4]. Furthermore, OFDM is useful in modern applications, including F-OFDM, U-OFDM, GFDM, and COFDM. Despite these advantages, OFDM faces challenges associated with the high peak-to-average power ratio (PAPR) [4,5]. This can result in in-band (IB) and out-of-band (OOB) radiation, with the non-linear nature of the High Power Amplifier (HPA) used in the transmitter being a significant contributor to the problem [5,6]. The high PAPR also increases the complexity of using processing blocks such as analog-to-digital converters (ADCs) and digital-to-analog converters (DACs) [11]. Therefore, it is essential to address the PAPR issue. Instead of the classical solution of using an expensive amplifier with a large linear range, it is advisable to find a solution to reduce the PAPR [5-7]. Many techniques have been proposed to reduce the PAPR, which can be divided into two categories [5-8]. The first category consists of signal distortion techniques, including clipping [15], clipping and filtering [14], peak windowing [10], active constellation extension (ACE) [14], non-linear companding transforming [7,22], and trellis-assisted constellation subset selection (TACSS) [8]. The second category includes signal scrambling techniques, such as selective mapping (SLM) [16], partial transmit sequence (PTS) [19], block coding [14], tone reservation (TR) [17], and tone injection [7].

This paper focuses on the clipping method, which is a distinguished PAPR reduction technique that offers a simple and low-complexity solution. It reduces the PAPR to a predefined threshold [9-11]. The clipping technique allows signal peaks to be avoided by using an arbitrarily chosen threshold. However, an arbitrary threshold value can lead to signal distortion and compromise the effectiveness of the method in terms of peak reduction. This is a common issue in classical clipping approaches [14]. To address this issue, it is advisable to select a more appropriate amplitude value before applying the clipping action. This can be achieved using various estimation techniques, such as Pisarenko Harmonic Decom position (PHD), Multiple Signal Classification (MUSIC) [13,15], Root-MUSIC [15], and Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) [12].

In this paper, the MUSIC approach is used to analyze the dynamics of an OFDM signal and to determine an optimal clipping threshold. This approach aims to improve the efficiency of the PAPR clipping reduction method by selecting an appropriate threshold that improves performance while minimizing signal distortion. The paper is organized as follows. Section 2 describes the related work. Section 3 analyzes the proposed modelling. Results and discussions are debated in Section 4. Lastly, the paper’s conclusions are given in Section 5.

2. RELATED WORK

Reducing PAPR is a significant challenge in wireless communication systems that employ OFDM modulation. Over time, several techniques have been proposed to address this challenge while minimizing signal distortion and maintaining system efficiency. One commonly used technique is the conventional clipping method, which involves limiting the amplitude of the OFDM signal to a predefined threshold [9-11]. While this method effectively reduces PAPR, it can also introduce adverse effects such as distortion and interference, which can negatively impact overall communication quality [14]. Another technique is the encoding method, which entails encoding the data bits before modulating them into OFDM symbols. This approach reduces the probability of large peaks in the signal and subsequently reduces PAPR [20]. However, the encoding method can increase system complexity and introduce redundancy, which can lead to a decrease in overall data throughput. The selective mapping method (SLM) is another technique that generates multiple OFDM symbols from the same data block, each utilizing a different phase sequence. The system then selects the symbol with the lowest PAPR for transmission [16]. Although this method effectively reduces PAPR, it introduces some complexity. Successful implementation of the SLM method requires transmitting additional information to the receiver, which adds an extra cost to the system [16]. The Partial Transmission Sequence (PTS) technique is an alternative. method that involves dividing the OFDM symbol into multiple sub blocks and applying different phase factors to each sub block. This strategic manipulation aims to decrease the PAPR when combining the sub-blocks in the final signal [19]. However, this approach also introduces additional complexity to the system. To successfully implement the PTS method, extra information needs to be transmitted to the receiver, resulting in communication costs [19].

In recent years, various techniques have been proposed to enhance the performance of wireless communication systems in reducing PAPR. For instance, a PAPR reduction method based on deep learning was introduced in [21]. This method utilizes a deep neural network to predict and decrease PAPR in OFDM signals.

3. SIGNAL MODELING

3.1. Basic OFDM Signal Modeling

The OFDM sequence is generated by summing all N modulated subcarriers when applying the IFFT operation, the subcarriers may be orthogonal to each other [1-5]. To understand the concept of OFDM, let X = {Xk, k = 0, 1…, N − 1}, be the complex representation of the input data block symbols after the constellation mapping operation, where Xk represents the block data of the kth subcarrier from 1 to N. Therefore, the complex baseband OFDM signal is defined as:

Where ej2πk∆f t is the twist factor of the kth subcarrier, T is the total time of the symbol, ∆f is the frequency space between the subcarriers. The bandwidth of the symbol is B = N.∆f, and ∆f is set to 1/T to ensure the orthogonality between the subcarriers of the symbol [1,2]. The baseband OFDM signal is sampled using the Nyquist rate (t = T /N). Therefore, the discrete OFDM signal can be expressed in the time domain as:

where n is the discrete sampling index, and the discrete OFDM signal vector is written as:

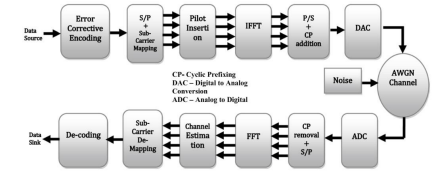
The principle of the OFDM system is shown in Figure 1. At the transmitter end, the input data is mapped by one of the modulation (Mod) schemes [4]. The signal is then converted from serial to parallel (S/P). An IFF is then applied. A cyclic prefix is added to the signal. The cyclic prefix adds a copy of the end of the OFDM symbol to its beginning, then the received signal is converted from parallel to serial (P/S) before being transmitted to the channel [5]. At the receiver side, the received signal is converted from S/P and demodulated by FFT. Then the signal is converted from P/S and demodulated to obtain data output as shown below:

Figure 1. OFDMTransmitterandReceiverBlock Diagram

3.1. PAPR in OFDM System

The presence of peaks in an OFDM signal corresponds to a high PAPR [5]. PAPR is defined as the ratio of the maximum peak power to the average power of the signal, as expressed in equation 4:

E{.}is the average power of the signal. The continuous-time representation of the OFDM signal is obtained by applying the oversampling operation. This operation ensures that peaks not captured in the PAPR calculation are taken into account [6]. To improve the accuracy of the PAPR calculation, the discrete baseband signal is sampled with L ≥ 4 by inserting (L−1) N zero padding between samples, where L is the oversampling factor. As a result, the oversampled OFDM signal is written as [3]:

The evaluation of the performance of PAPR is commonly done using the Complementary Cumulative Distribution Function (CCDF) [6]. The CCDF represents the probability of the PAPR value exceeding a specific threshold. According to the central limit theorem [5], when there is a large number of subcarriers N, the real and imaginary parts of the OFDM signal in the time domain follow a Gaussian distribution with a mean of zero and a variance of 0.5. To calculate the CCDF of the time-domain signal at the Nyquist sampling rate, the appropriate formula is used. [14]:

Where PAPR0 is the threshold value. Furthermore, when oversampling L is conducted, the CCDF of the OFDM signal can be written as [3-6]:

The CCDF curves of the PAPR performance can be used to compare the effectiveness of different PAPR reduction techniques [4]. A lower CCDF curve indicates a lower probability of having a high PAPR value, which means a better PAPR reduction [3-6].

3.2. Classical Clipping

In this section, we explore classical clipping technique used to reduce the PAPR value[14]. As it was formerly indicated, the classical clipping retains a predistortion technique used to reduce the PAPR in OFDM systems [9,10]. The basic idea is to trim the peak of the OFDM signal above a given named CR (Clipping Ratio) threshold. In this paper such clipping can be expressed as [11- 14]:

Where:

xc(n) represents the clipped output signal

x(n) is the input OFDM signal at time n

CR is a threshold. It defines the limit value beyond which the samples of the signal x(n) will be
clipped.

3.3. Contribution

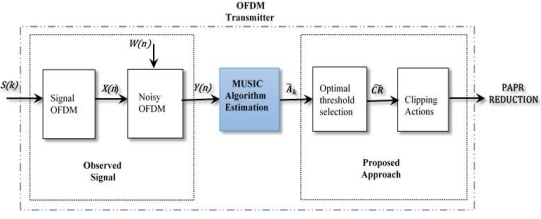
To effectively apply clipping to a signal x, it is essential to have a deep understanding of the signal’s dynamics. However, in many cases, the clipping threshold is arbitrarily set without proper justification, which may not accurately reflect the true characteristics of the signal, as highlighted in [14]. To address this, an estimation approach can be employed to make a more informed selection of the threshold. By utilizing the MUSIC algorithm, a more accurate clipping can be applied to the signal, leading to a better assessment of its effects [13,15].

The MUSIC algorithm, renowned for its spectral analysis capabilities, is employed to achieve a higher resolution of the signal’s dynamics. It is noteworthy that the signal subspace technique heavily relies on the covariance matrix, as discussed in [18]. This matrix is utilized to extract information about the signal subspace from the OFDM signal, facilitating the separation of signal components from different subcarriers and the reduction of noise. To estimate the signal, an Eigen Decomposition of the noisy observed signal is performed, dividing it into two subspaces [18]. In comparison, while the ESPRIT algorithm is more computationally efficient due to its avoidance of spectral searches, MUSIC offers superior accuracy in identifying closely spaced frequencies, which is crucial for resolving the fine spectral details in OFDM signals. Additionally, MUSIC provides higher resolution and robustness to noise, making it well-suited for applications where precision in frequency estimation and the separation of subcarriers are critical for accurate signal reconstruction.

Figure 2 bellow summarizes our contribution:

Figure 2. Proposed Method

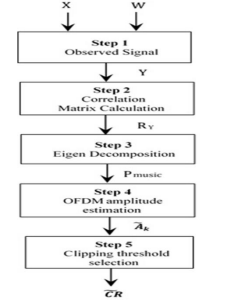
The flowchart of the proposed method, based on the MUSIC algorithm, is illustrated in Figure 3:

Figure 3. Proposed Method Flowchart using MUSIC Algorithm

Step1. Observed Signal

We have the mixture of signal OFDM, x(n), and additive noise, w(n), with variance σ2 at the observation, y(n)

𝑦(𝑛) = 𝑥(𝑛) + 𝑤(𝑛) (8)

Where x(n) contains N subcarriers.

where Ak, fk are amplitude and frequency respectively of the kth subcarriers.

Step2.Correlation Matrix Calculation

Based on the observed signal defined by (8), the related autocovariance matrix can be obtained by:

With the Toplitz matrices, the auto covariance matrix can also be written as:

Where Rx, I and H are autocovariance matrix for x, identity matrix and the Hermitian transpose respectively and Rw = σ2 I. So, Rx can be written as:

So we have:

Where PK represents the powers set of various OFDM subcarriers. It is possible to extract all the parameters relating to x from the eigenvalues and eigenvectors by the Eigen Decomposition of Ry described in the next step.

Step3. Eigen Decomposition

The MUSIC method relies on the Eigen Decom position where the eigenvalues of Ry are ordered as λ1> λ2 > λ3… >λM. In the noise free case, the eigenvalues λ1,λ2,λ3 …λN are non-zero and the eigenvalues λN+1,λN+2,…,λM are zero. The Eigen Decomposition of autocovariance matrix of Ry can be written as:

R = UΛU ^H (16)

Where U is the matrix of eigenvectors, Λ is the diagonal matrix containing the eigenvalues.

Step4. OFDM amplitudes estimation

The amplitudes of the OFDM signal are estimated by focusing on the eigenvalues associated with the signal subspace. The larger eigenvalues, corresponding to the first N values (N < M), indicate the presence of the signal. Conversely, the remaining (M − N) smaller eigenvalues represent the noise. The orthogonal nature of the noise eigenvalue, with each column of the matrix representing the signal subspace, is exploited. Since each row of this matrix corresponds to a source signal, the orthogonality simplifies the identification of the subcarriers associated with the source signal. Consequently, the first rows of the matrix are dedicated to the source signal, while the subsequent rows represent the noise. By equation (15) and (17), we have:

The signal subspace is: Ux=span {u1, u2,…,uN}. The noise subspace, is orthogonal to signal subspace: Uw= span{uN+1,uN+2,…,uM}.

So, we can deduce the MUSIC Spectrum as:

As a result, the estimated amplitudes can also be deduced from the signal powers Pmusic(k) as follows:

Step5.Clipping threshold selection

To select an optimal threshold 𝐶𝑅̃ we have used the amplitudes estimates 𝐴̃𝑘as:

Where:

• 𝐴̃𝑘: These are the estimated amplitudes of the OFDM subcarriers, derived from the MUSIC spectrum (Equation 24).
• 𝑚𝑒𝑎𝑛(𝐴̃𝑘) : This represents the average value of all the estimated amplitudes. The mean gives a general idea of the overall strength of the signal across all subcarriers.
• max(𝐴̃𝑘): This is the maximum value among the estimated amplitudes, identifying the strongest subcarrier in terms of amplitude.

𝐶𝑅̃ helps define a clipping threshold that balances between the average signal level and the strongest signal component. The idea is to avoid excessive clipping, which can distort the signal, while ensuring that weaker signals are still adequately captured.

The proposed approach is also described in Algorithm1 below:

4.RESULTS AND DISCUSSIONS

This section presents the simulation results used to evaluate the performance of the proposed PAPR reduction technique. The simulations were conducted using 64 subcarriers, with Differential Phase Shift Keying (DPSK) symbols input into the OFDM system. A Monte Carlo simulation was performed to assess the effectiveness of the proposed method.

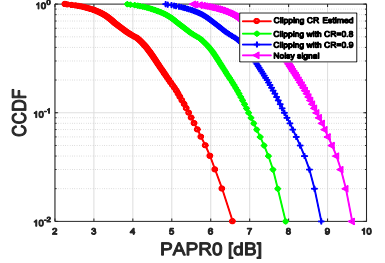
The simulation results show that the proposed PAPR reduction technique outperforms the traditional approach. Figure 4 compares the PAPR between the proposed method and conventional clipping. At a clipping threshold of 0.9, the proposed technique achieves an improvement of approximately 2.5 dB over the conventional approach, as indicated by the PAPR CCDF at 10−2.Additionally, compared to the original OFDM system, the proposed method successfully reduces the PAPR by approximately 3.5dB.

Figure 4.PAPR performance based on proposed scheme

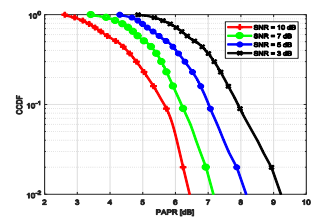
Figure 5 bellow illustrates the Complementary Cumulative Distribution Function (CCDF) of the PAPR for SNRs ranging from 3 dB to 10 dB. The results clearly show that as the SNR increases, the PAPR decreases, suggesting that systems operating at higher SNRs experience less pronounced signal peaks relative to the average power.

Figure 5. . PAPR performance of OFDM with different SNR

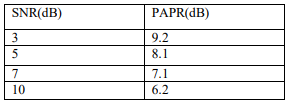
Table 1 quantifies the relationship between SNR and PAPR. The measured PAPR values for SNRs. These results further confirm the trend observed in the CCDF curves: as SNR increases, the PAPR reduction becomes more effective.

Table 5. PAPR values with various SNR

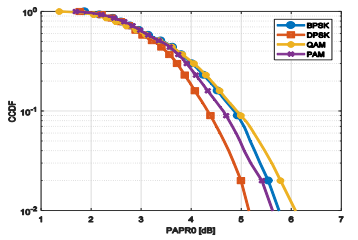
To enhance the effectiveness of our proposed method, we conducted additional simulations by varying the modulation type and the number of subcarriers. Figures 6 and 7 present the results. Figure 6 displays the CCDF curves of the PAPR for BPSK, DPSK, QAM, and PAM modulation schemes under identical conditions, using 64 subcarriers and a SNR of 10 dB. At a CCDF level of 10−2, the PAPR values are: DPSK (3.4 dB), PAM (3.8 dB), BPSK (4.2 dB), and QAM (4.8 dB).

DPSK exhibits the lowest PAPR due to its differential encoding, which smooths transitions between symbols. PAM shows a slightly higher PAPR due to occasional increases in signal peaks from a lack of phase continuity. BPSK has a marginally worse PAPR due to abrupt phase changes. QAM has the highest PAPR due to simultaneous modulation of phase and amplitude, causing significant signal fluctuations.

So, DPSK offers the best PAPR performance, followed by PAM. BPSK shows a higher PAPR, and QAM has the highest PAPR, requiring careful management in power-constrained systems

Figure 6. PAPR performance of OFDM with differents modulation type

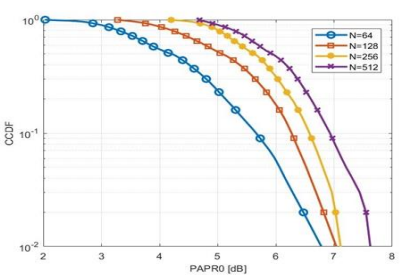
In Figure 7 we examined the PAPR in an OFDM system with varying numbers of subcarriers. The results show that PAPR increases as the number of subcarriers grows. This behaviur is to be observed, as the probability of large peaks in the transmitted signal increases in direct proportion to the number of subcarriers. As the number of subcarriers is increased, the OFDM signal becomes a sum of a greater number of independent modulated signals, which increases the likelihood of constructive interference and thus results in higher PAPR values. This trend serves to illustrate the difficulties inherent in PAPR reduction for systems comprising a considerable number of subcarriers, a configuration that is becoming increasingly prevalent in modern communication standards, including 5G and beyond.

Figure 7. PAPR performance of OFDM with differents Number of subcarriers

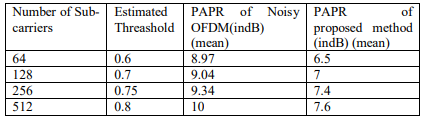
Table 2 summarizes how our approach reduces PAPR by an average of 2.75 dB to 3.34 dB, depending on the number of subcarriers. It also highlights that the clipping threshold increases with more subcarriers, indicating higher clipping levels for larger OFDM signals.

Table 2. PAPR values with various subcarriers

5.CONCLUSIONS

This research introduces a novel and effective approach to reducing the peak-to-average power ratio (PAPR) in OFDM systems, achieving a substantial reduction of 3.5 dB compared to the original OFDM and 2.5 dB compared to conventional clipping methods. A significant contribution of this research is the integration of the Multiple Signal Classification (MUSIC) algorithm for the estimation of the dynamic range of the OFDM signal. By accurately assessing the signal dynamics, the MUSIC algorithm enables the precise determination of the optimal clipping threshold, thereby achieving a balance between PAPR reduction and signal distortion minimisation. The deployment of the MUSIC algorithm guarantees that the clipping threshold is dynamically calibrated in accordance with the estimated characteristics of the OFDM signal, thereby facilitating more efficient PAPR reduction without the introduction of excessive distortion. This approach not only enhances the performance of power amplifiers by reducing power consumption but also preserves the integrity of the transmitted signal, thereby improving both efficiency and reliability in wireless communication systems. The results demonstrate the potential of the proposed method to significantly enhance the performance of OFDM systems, rendering it highly applicable in modern wireless communication networks where power efficiency and signal quality are paramount. Moreover, the techniques developed in this study can be extended to a range of wireless communication technologies, particularly as they evolve towards more complex and bandwidth-intensive standards, such as 5G and beyond. The combination of MUSIC-based dynamic range estimation with adaptive clipping offers significant advantages in PAPR reduction across a range of platforms.

CONFLICTS OF INTEREST

The authors declare no conflict of interest.

REFERENCES

[1] Javier Lorca Hernando, Ana García Armada “Frequency-Modulated OFDM: A New Waveform for High-Mobility Wireless Communications” in IEEE transactions on communications, VOL. 71, NO. 1,2023;

[2] F. Conceição, M. Gomes, V. Silva, R. Dinis, A. Silva, and D. Castanheira, “A Survey of Candidate Waveforms for beyond 5G Systems” in Electronics, vol. 10, no. 1, p. 21, 2021.

[3] N. A. Galande and A. M. Shah, “Implementation of OFDM by using wavelet for optimization of wireless communication system,” in IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), 2016.

[4] A. Darghouthi, A. Khlifi, H. Shaiek, F. B. Salah, and B. Chibani, “A Hybrid Framework OTFSOFDM Based on Mobile Speed Estimation” in International Journal of Computer Networks and Communications(ijcnc) 16(3):49-67, 2024.

[5] F. B. Salah, A. Khlifi, M. Rjili, and B. Chibani, “PAPR Reduction Based on FrFT in OFDM Systems,” SSD 2024, vol. 745, pp. 745-749, 2024.

[6] U. S.M. and M. H.B., “A new approach to improve the performance of OFDM signal for 6G communication,” International Journal of Computer Networks & Communications (IJCNC), vol. 14,

[7] B. Adebisi, K. Anoh, and K. M. Rabie, “Enhanced nonlinear companding scheme for reducing PAPR of OFDM systems,” in IEEE Syst. J., vol. 13, no. 1, pp. 65–75, Mar. 2019.

 [8] K. Liu, L. Wang, and Y. Liu, “A new nonlinear companding algorithm based on tangent linearization processing for PAPR reduction in OFDM systems,” in China Commun, vol. 17, no. 8, pp. 133–146, Aug. 2020.

 [9] Z. Xing, K. Liu, A. S. Rajasekaran, H. Yanikomeroglu, and Y. Liu, “A hybrid companding and clipping scheme for PAPR reduction in OFDM systems,” in IEEE Access, vol. 9, pp. 61565–61576, 2021.

[10] Liu & al “An Enhanced Iterative Clipping and Filtering Method Using Time-Domain Kernel Matrix” in IEEE Access, 2019.

[11] F. B. Salah, A. Khlifi, M. Rjili, and B. Chibani, “PAPR Reduction in OTFS Systems Using Multi Weighted Fractional Fourier Transform Analysis,” HSI 2024, pp. 1-6, 2024.

[12] Liu & al “An Improved ESPRIT Algorithm for DOA Estimation of Coherent Signals” in IEEE Access,2019.

[13] C Liu, X Cheng, J Su, Y Yuan “Research and Simulation of Super resolution Root-MUSIC Algorithm” in 4th International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), 2023.

 [14] S. S. Haque and M. M. Mowla, “Performance improvement for PAPR reduction in LTE downlink system with elliptic filtering,” Int. J. Comput. Netw. Commun(IJCNC)., vol. 7, no. 1, pp. 1-10, Jan. 2015.

[15] Jin& al “Improved MUSIC algorithm for frequency estimation” in Signal, Image and Video Processing, 2017.

[16] M. A. Taher & al “Sliding the SLM-technique to reduce the non-linear distortion in OFDM systems”, in Elektrotechn, 2014.

[17] H. Liang & al “PAPR of orthogonal frequency division multiplexing systems using modified tone reservation techniques”,in IJCS,2016

[18] Aidan O. T. Hogg; Vincent W. Neo; Stephan Weiss; Christine Evers “A Polynomial Eigenvalue Decomposition Music Approach for Broadband Sound Source Localization” in IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA),2021.

[19] R. P. S. M. Pallavi, G. Rajalakshmi, and S. R. Mahadeva Prasanna, “Efficient PAPR Reduction in OFDM Systems Using Modified PTS Scheme,” IEEE Access, vol. 9, pp. 30497-30504, 2021

[20] J. Wang, Z. Ma, and D. Qu, “Joint Source-Channel Coding and PAPR Reduction Scheme for OFDM Systems,” IEEE Transactions on Communications, vol. 71, no. 2, pp. 887-898,2023

[21] S. Chen, X. Zhang, and C. Zhao, “PAPR Reduction in OFDM Systems Using Deep Learning,” IEEE Access, vol. 8, pp. 57580-57589, 2020.

[22] M. M. El-Nabawy, M. A. Aboul-Dahab, and K. El-Barbary, “PAPR Reduction of OFDM Signal by Using Combined Hadamard and Modified Meu-Law Companding Techniques,” International Journal of Computer Networks & Communications (IJCNC), vol. 6, no. 5, pp. 71-84, Sep. 2014

AUTHORS

Fatma BEN SALAH, born in Gafsa, Tunisia, in 1989, earned her Bachelor’s degree in Engineering in 2014 from the National School of Engineers of Gabes(ENIG), with a specialization in Communication and Networking. Presently, she is pursuing her doctoral studies in Telecommunication Networks. Fatma is currently a contracted professor at ENIG, where she imparts her knowledge and expertise to students.

Abdelhakim KHLIFI serves as an assistant professor at the National Engineering School of Gabes, Tunisia. He earned his Engineer degree in 2007, followed by a Master’s degree from the National Engineering School of Tunis in 2010, and a Ph.D. degree in 2015. His teaching specializes in signal processing and digital communications. His primary research interests center on the performance analysis of waveform optimization in 5G/6G systems.

Marwa RJILI born in Medenine, Tunisia, in 1991, obtained her Bachelor’s degree in Engineering in 2014 specializing in Communication and Networking. She is currently a doctoral student in Electrical Engineering at the same institution. Additionally, Marwa serves as a contractual lecturer at the Higher Institute of Computer Science and Multimedia of Gabes.

Amina Darghouthiborn in Tozeur, Tunisia, in 1993, is a doctoral student researcher in Electrical Engineering at the National Engineering School of Gabes (Tunisia). Additionally, Amina serves as a contractual lecturer at the National School of Engineers of Gabes, sharing her knowledge and expertise with students.

RHAIMI Belgacem Chibani is an Associate Professor in Computer Sciences & Information Engineering (CSIE). He has been employed at the National Engineering High School at Gabes (ENIG) since September 1991. After earning his Doctorate Thesis at the National Engineering High School at Tunis (ENIT), he received his Ph.D. degree from ENIG, University of Gabes, Tunisia, in 1992. He is a member of the Research Laboratory MACS at ENIG, where he serves as an activities supervisor in the field of Signal Processing and Communications Research. Currently, his research areas encompass Signal Processing and Mobile Communications. He is affiliated with the University of Gabes, and his research interests include Information and Signal Processing, as well as Communications Engineering. He has published numerous papers in international conferences and journals, such as CESA, IFAC, autumn, spring, A2I, and Summer Schools. Additionally, he is a member of the Communications Engineering staff at ENIG and has served as a Program Committee Member for various top national schools and activities related to Communications.