IJCNC 04

FUZZY-BASED CLUSTERING OF WIRELESS SENSOR NETWORKS FOR MULTIPLE MOBILE AGENT ITINERARY PLANNING

Nidhi Kashyap1 , Shuchita Upadhyaya1 ,Monika Poriye*1 , Sachin Lalar2

1 Department of Computer Science and Applications, Kurukshetra University, Kurukshetra, India

4Department of Engineering and Technology, Gurugram University Gurugram

ABSTRACT

Mobile agent (MA) technology exhibits remarkable efficiency when integrated into Wireless SensorNetworks (WSNs) for information processing tasks. MAs reduce network overhead by executing processing code locally on nodes and selectively transmitting significant data to designated remote sensor nodes, thereby enhancing data fusion and acquisition while minimizing energy depletion. However, in large-scale networks, relying on a single MA leads to significant delays, necessitating the use of multiple MAs to operate asynchronously and minimize latency. The challenge lies in effectively grouping nodes to ensure MAs reach their intended destinations.

To address this challenge, this paper introduces a novel approach, the Adaptive FCM Clustering Algorithm (AFCM), a fuzzy-based clustering algorithm designed for addressing network partitioning challenges in Multiple Mobile Agent Itinerary Planning (MIP). A systematic analysis of the existing literature examines various MIP algorithms, emphasizing their strengths and uncovering potential research gaps. AFCM is specifically developed to create disjoint and load-balanced partitions tailored for multi-mobile agent itinerary planning. A Methodical analysis with three traditional clustering algorithms is conducted. The correctness of the Adaptive Fuzzy C-Means (AFCM) algorithm is demonstrated through a detailed manual application on a wireless network comprising 15 nodes.

KEYWORDS
Clustering, Itinerary planning, Mobile agent, Routing, Wireless sensor network.

1. INTRODUCTION

Mobile agents are software agents capable of autonomously migrating with their processing code and data state to perform specified data processing tasks for remote users [1], [2]. They can resume execution even after disconnection and process data at designated nodes. This flexibility allows them to efficiently utilize network bandwidth, conserve energy, and minimize latency [3], [4], [5], [6]. However, the deployment of mobile agents is only necessary when dealing with substantial amounts of data transmission. In traditional Wireless Sensor Networks (WSNs), deploying numerous sensor nodes in close proximity often leads to redundant sensed data. Transmitting this redundant data individually consumes significant energy and bandwidth [7], [8], [9], [10], [11]. In contrast, mobile agents migrate to each node, process and accumulate reduced data in their payload, and perform aggregation with previously accumulated and newly retrieved data [12], [13], [14]. By delivering only processed and aggregated information to the intended node, mobile agents enable accurate decision-making based on significant information.

Despite its numerous benefits, mobile agent (MA) technology also presents challenges, with mobile agent routing being a prominent issue [15], [16], [17], [18]. Routing mobile agents involves determining their optimal itinerary, which includes the sequence of migration and the group of nodes to be visited. The itinerary must be carefully planned to ensure that the collaborative system performs better than the traditional system. The problem is divided into three steps to address this:

• dividing the network into appropriate and disjoint clusters
• creating a group of source nodes to be visited within a single itinerary
• deciding the visiting order for completing their tasks

This research paper addresses the initial step of the stated problem, which involves partitioning the network into disjoint domains.To address this challenge, the study introduces an algorithm that partitions a Wireless Sensor network into distinct, non-overlapping domains, thereby improving the efficiency of the mobile agent system.

The proposed algorithm introduces a novel approach for autonomously determining the cardinality for network segmentation. It dynamically selects the optimal number of domains (clusters) and effectively partitions the network into non-overlapping, disjoint segments. Additionally, the algorithm adeptly resolves the challenge of assigning nodes equidistant from two centroids to the correct domain, ensuring precise network segmentation.

2. LITERATURE REVIEW

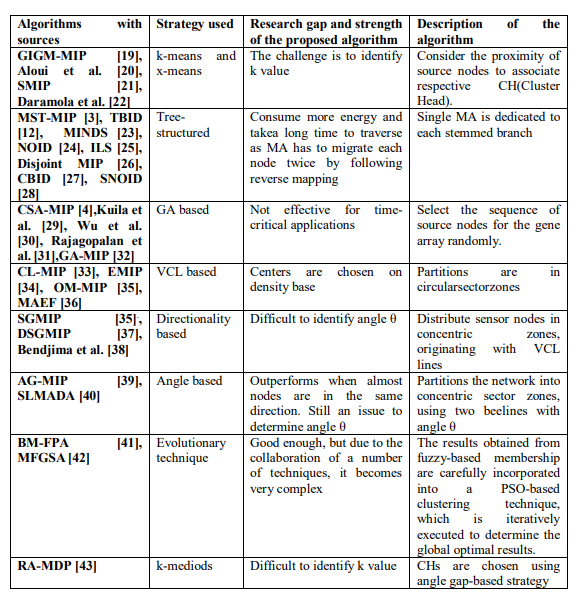
This research investigates the use of the mobile agent paradigm for Wireless Sensor Networks (WSNs) in communicating data. The mobile agent paradigm offers advantages such as efficient resource utilization, reduced network bandwidth usage, improved scalability, and offline stability. However, the effective operation of mobile agents requires careful planning of their migration path to avoid energy consumption and delays. Path determination can be achieved through static or dynamic itinerary planning. Static planning is suitable for known node sequences in physical data monitoring, while dynamic planning is used for target tracking with mobile and evolving targets. Table 1 presents a summary of the literature reviewed in this study, outlining the main findings and methodologies explored.

Table 1Clustering Techniques in Wireless Sensor Networks: A Review of Relevant Studies

The review of literature, detailed in Table 1, highlights different algorithms employed for network partitioning in multiple Mobile Agent Itinerary Planning (MIP), each with its unique advantages and limitations. Building on these observations, this study presents a new approach with the Adaptive FCM Clustering Algorithm, designed to generate disjoint and balanced partitions tailored for multi-mobile agent itinerary planning.

This research paper addresses the challenges of clustering in context to Mobile Agent routing in Wireless Sensor Networks, specifically focusing on issues related to overlapping and load balancing. The paper introduces the proposed AFCM algorithm and compares it with three traditional clustering algorithms. To validate the algorithm, a manual demonstration is provided using a 15-node wireless network. Additionally, the algorithm was implemented in Python to further verify its accuracy, and the results supported its correctness. The conclusions and findings of these investigations are discussed in the concluding section of the paper.

3. ENHANCING MULTI-MOBILE AGENT ITINERARY PLANNING: INTRODUCING AN ADAPTIVE FUZZY C-MEANS ALGORITHM FOR NETWORK CLUSTERING

After conducting a review of existing literature on multi-mobile agent itinerary planning (MIP), it was observed that network clustering plays a crucial role in achieving efficient MIP. Various algorithms, including k-means, x-means, tree-based, genetic algorithm-based, center locationbased, and directional based approaches, have been proposed to partition the network and optimize MIP.

The main drawback of the k-means clustering algorithm is its requirement to specify the number of clusters beforehand. Variants such as x-means and Fuzzy c-Means (FCM) are built upon the kmeans framework. In x-means clustering, an initial minimum number of centroidsis assumed, and clusters are subsequently adjusted to achieve optimal configuration. FCM algorithms, on the other hand, start with a fixed number of clusters and iteratively update centroids while assigning data points to clusters based on membership values to optimize results. Although x-means, kmeans, and FCM share some characteristics, FCM is distinguished as a prominent soft clustering method, allowing data points to belong to multiple clusters simultaneously according to their membership degrees.

However, Fuzzy c-Means (FCM) encounters challenges when a sensor node has equal membership values for multiple destination itineraries, potentially resulting in imbalanced domains within multi-mobile agent itinerary planning (MIP) systems. To address this issue, this paper proposes a revised version of the FCM algorithm, termed Adaptive Fuzzy C-Means (AFCM), designed to improve network clustering in MIP applications.

The AFCM algorithm addresses the issue of imbalanced domains by associating each sensor node with the Domain Initial (DI) that has the lower expected load. This method helps to balance the domains, thereby enhancing the efficiency of multi-mobile agent itinerary planning (MIP) systems. The research will assess the AFCM algorithm’s capability to manage cases where sensor nodes have equal membership values for multiple DIs and evaluate its effectiveness in creating balanced domains.

By overcoming the limitations of existing clustering algorithms, particularly Fuzzy C-Means (FCM), the proposed study aims to improve the performance and efficacy of MIP systems. The evaluation of the AFCM algorithm’s performance in network clustering for MIP will contribute to the advancement of more effective itinerary planning techniques in multi-agent systems.

3.1. Distinguishing Clustering Algorithms: Exploring AFCM’s Motivation and Uncovering Algorithmic Differentiations

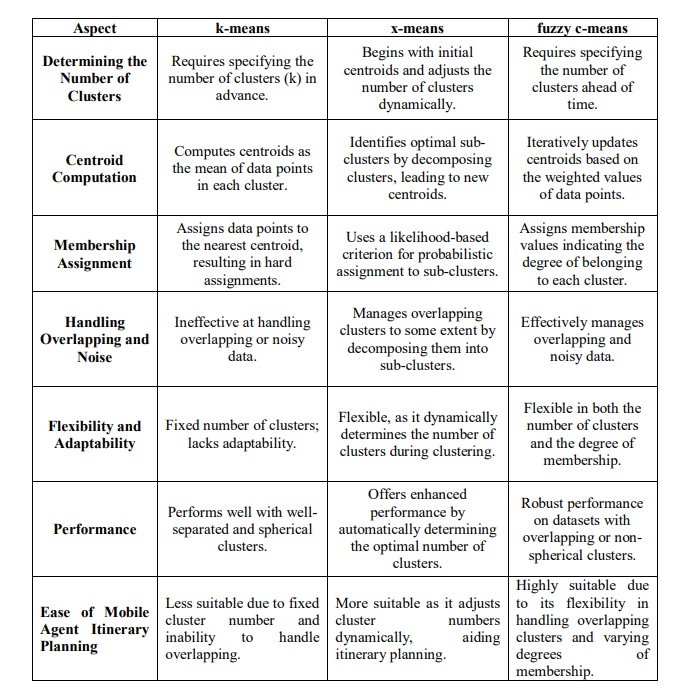
Table 2 offers a detailed comparison of the k-means, x-means, and fuzzy c-means clustering algorithms. This analysis aims to clarify the reasons for introducing the Advanced Fuzzy CMeans (AFCM) algorithm. By highlighting the unique characteristics and limitations of each algorithm, the table helps to identify the specific strengths and weaknesses that drive the development of AFCM as a novel approach in clustering techniques.

Table 2: Comparison between k-means, x-means, and fuzzy c-means clustering algorithms

This table offers a succinct overview of the primary distinctions among the algorithms. It is important to note that their performance can vary based on the particular dataset and the nature of the clustering task.

3.1.1. Description of the Adaptive Fuzzy C-Means (AFCM) Clustering Algorithm for Sensor Networks

This section provides a detailed, point-by-point description of the Adaptive Fuzzy C-Means (AFCM) Clustering Algorithm, tailored for use in Sensor Networks

1. AFCM approach: The Adaptive Fuzzy C-Means (AFCM) Clustering Algorithm for Sensor Networks operates without the need to specify the number of clusters (k) in advance.

2.Selection of processing node (PE): AFCM selects a centralized processing node (PE) within the network.
3. Determining k: The number of Sensor Nodes (SNs) in the vicinity of the PE becomes the value of k. These SNs are referred to as domain initials (DI).
4. Assignment of Remaining Sensor Nodes (SNs): The remaining sensor nodes are allocated to the domain initials (DIi) within the set DI. For each remaining sensor node, the membership value (µi, j) is computed relative to each domain initial (DIi) in its vicinity.
5. Sum of membership values: The sum of membership values (∑ µi, j) of each remaining SN with respect to each DIi is calculated in advance.
6. Calculation of Sum of membership values: The total sum of membership values (∑ µi, j) for each remaining sensor node (SN) with respect to each domain initial (DIi) is computed beforehand.
7. Assignment to Domain Initials (DIi): Each sensor node is allocated to the domain initial (DIi) that has the highest membership value. After each assignment, the sum of membership values (∑ µi, j) is recalculated.
8. Finalizing Assignments: The assignment process continues until all sensor nodes in the network are allocated to a designated domain initial (DIi). For nodes that have identical membership values across multiple DIs, they are assigned to the DIi with the lowest total sum of membership values (∑ µi, j).
9. Threshold Comparison: The updated sum of membership values (∑ µi, j) is compared against a predefined threshold, which represents the minimum value required for deploying a single Mobile Agent (MA). Domain initials (DIi) with ∑ µi, j values falling below this threshold are excluded from further consideration.
10. Domain Reduction: To minimize the number of domain initials (DIs) or DIi, existing domain initials and their assigned nodes are consolidated. This merging process facilitates the creation of non-overlapping, load-balanced domains, ensuring a more efficient distribution of sensor nodes.

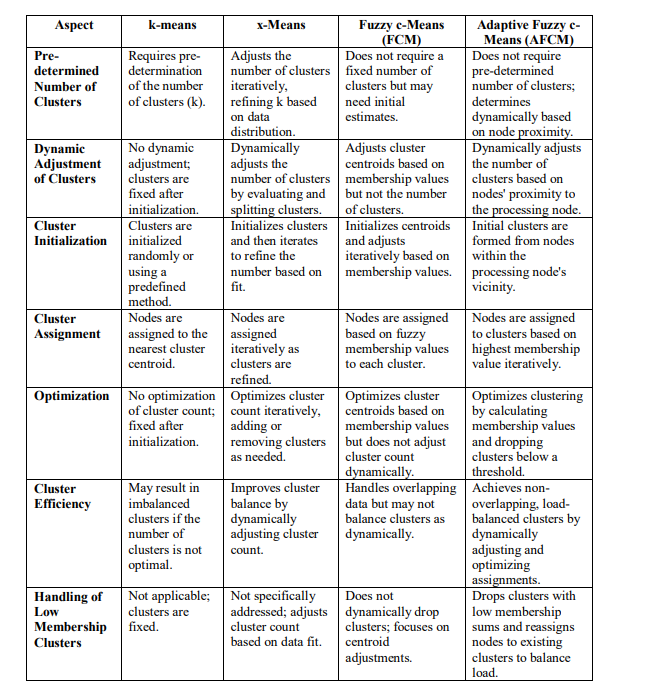
3.1.2. Distinctive Features of the Adaptive Fuzzy C-Means (AFCM) Algorithm in Comparison to k-means, x-Means, and Fuzzy c-Means (FCM)

1. Requirement for Cluster Number Specification:

• k-means: Requires an explicit specification of the number of clusters prior to execution, which can limit its adaptability to diverse data distributions.

• x-Means: Addresses the limitation of fixed cluster numbers by iteratively adjusting and refining the number of centroids based on data characteristics.

• Fuzzy c-Means (FCM): Does not necessitate a fixed number of clusters from the outset, but still relies on initial estimates that can influence clustering outcomes.

• Adaptive Fuzzy c-Means (AFCM): Advances beyond these methods by determining the number of clusters dynamically, based on the proximity of nodes to a central processing node, thus eliminating the need for pre-specified cluster numbers.

2. Cluster Initialization:

• k-means: Initializes clusters either randomly or through a predefined method, which may not always align with the data distribution.

• x-Means: Starts with an initial cluster configuration and iteratively adjusts the cluster count to enhance data fit.

• Fuzzy c-Means (FCM): Initiates with centroids and iteratively refines them based on membership values, though initial cluster estimates still play a role.

• AFCM: Uniquely establishes initial clusters (domain initials) using nodes in proximity to the processing node, thus aligning initial clusters more closely with local data characteristics.

3. Cluster Assignment Method:

• k-means: Assigns nodes to the nearest centroid, potentially leading to imbalanced clusters if the initial number of clusters is suboptimal.

• x-Means: Iteratively refines cluster assignments as the number of clusters is adjusted, improving alignment with data distribution.

• Fuzzy c-Means (FCM): Utilizes fuzzy membership values to assign nodes to clusters, allowing for partial membership but not necessarily optimizing cluster count.

• AFCM: Assigns nodes to clusters based on the highest membership value in aniterative manner, ensuring effective and balanced allocation of all nodes.

4. Clustering Optimization:

• k-means: Does not perform dynamic optimization of cluster numbers after initialization, which can lead to inefficiencies if the fixed number of clusters is not ideal.

• x-Means: Enhances clustering by iteratively optimizing the number of clusters, adapting based on data fit.

• Fuzzy c-Means (FCM): Focuses on centroid optimization according to membership values but does not dynamically adjust the number of clusters.

• AFCM: Provides a sophisticated optimization approach by calculating the sum of membership values in advance. It discards clusters with low membership sums and redistributes nodes to remaining clusters, resulting in non-overlapping and load balanced domains.

5. Handling Low Membership Clusters:

• k-means: Fixed clusters remain unchanged regardless of membership distribution, which may not address low membership issues.

• x-Means: Adapts the number of clusters based on data fit but does not specifically address low membership clusters.

• Fuzzy c-Means (FCM): Concentrates on refining centroid positions without dynamically adjusting or eliminating low membership clusters.

• AFCM: Actively manages clusters with low membership sums by eliminating them and reassigning their nodes, thereby optimizing clustering efficiency and balance

In summary, the AFCM algorithm offers significant improvements over k-means, x-Means, and FCM by dynamically determining the number of clusters based on node proximity, optimizing cluster assignments, and achieving more balanced and efficient clustering in sensor networks.

Table 3 gives a comprehensive comparison that includes all aspects for k-means, x-Means, Fuzzy c-Means (FCM), and Adaptive Fuzzy c-Means (AFCM)

Table 3: Comprehensive Comparison of k-means, x-Means, Fuzzy c-Means (FCM), and Adaptive Fuzzy c-Means (AFCM): Key Aspects and Distinctive Features

3.1.3. Comparative Analysis of Fuzzy c-Means (FCM) and Adaptive Fuzzy c-Means (AFCM) Algorithms: Advancements, Adaptability, and Efficiency

Comparing the Fuzzy c-Means (FCM) and Adaptive Fuzzy c-Means (AFCM) algorithms is crucial for understanding their respective strengths and advancements in clustering research. While FCM requires pre-determined cluster numbers and operates with static cluster adjustments, AFCM introduces dynamic cluster determination based on node proximity, significantly enhancing its adaptability to varying data distributions. This dynamic approach allows AFCM to optimize clustering through iterative membership calculations and cluster reduction, leading to more balanced and efficient clustering outcomes compared to FCM. Additionally, evaluating these algorithms helps identify their suitability for different applications, particularly in scenarios requiring dynamic adjustments and efficient resource management. Overall, this comparison highlights AFCM’s practical advantages in handling dynamic and resource-sensitive clustering
tasks more effectively than FCM.

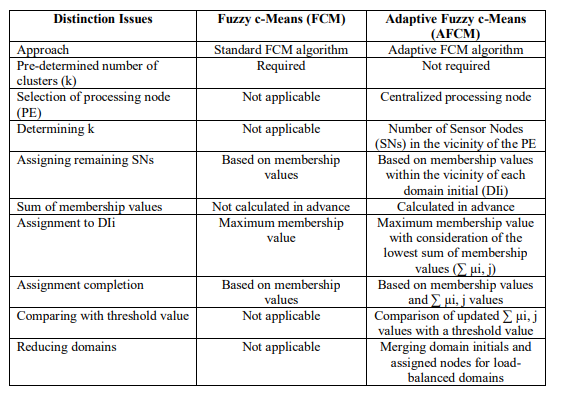
Table 4 offers a concise yet thorough comparison between the Fuzzy c-Means (FCM) and Adaptive Fuzzy c-Means (AFCM) algorithms, highlighting their key differences and demonstrating the advantages of AFCM over FCM.

Table 4: Distinctions between Fuzzy C-Means (FCM) and Adaptive Fuzzy C-Means (AFCM) algorithms

These distinctions highlight the key differences between the FCM and AFCM algorithms, emphasizing the adaptive nature of AFCM, which does not require pre-determining the number of clusters (k) and incorporates additional steps for processing node selection, assignment completion, and domain reduction to achieve load-balanced domains in sensor networks.

4. ADAPTIVE FUZZY-BASED CLUSTERING ALGORITHM (AFCM): A COMPREHENSIVE DESCRIPTION

The proposed algorithm addresses critical challenges in clustering, such as load balancing and cluster overlapping. Unlike traditional set theories, fuzzy-based partitioning captures the degree of belongingness of each sensor node (SN) to the network. Equation 1 illustrates that the degree of membership (µ) represents the similarity between nodes. Sensor nodes are grouped based on the domain initial (DI) with the highest µi,j value, where µi,j∈ [0, 1]. Nodes near the center have higher µ values, while those near the boundary have lower µ values. The algorithm utilizes membership functions to map distances to degrees of membership (µi,j).

4.1. Objective and Methodology: Associating Source Nodes with Domain Initials

In a collaborative system, the processing element (PE) assigns mobile agents (MAs) to specific starting points known as domain initials (DIs), where DIi represents the candidate’s starting point for an MA’s journey. The set DI consists of source nodes that are within the transmission range of the PE.

The objective of the proposed algorithm is to associate source nodes with their corresponding DIs. This association ensures that for every source node i in the set SN (∀i∈ N), there exists a DIj in the set DI such that i is within the transmission range of j i.e. jrange. Any source nodes that are not directly associated with a DI are placed in the set NDA (not directly associated). The algorithm employs fuzzy-based clustering to determine the degree of association µi,j, calculated using equation 2. The clustering process follows the constraints specified in equations 3 and 4, ensuring exhaustive partitioning and disjointness among the DIs.

The value of ‘m’ can be adjusted adaptively.

• A lower value of ‘m’ results in sharper boundaries between clusters, making them more
  distinct.
• Conversely, a higher value of ‘m’ leads to softer boundaries between clusters, allowing
  for more overlap and uncertainty.

Equation 3 ensures that the total degree of association between each source node and the domain initials within its vicinity always adds up to one. This constraint guarantees the disjunction of any two domains, meaning that no source node is connected to more than one domain initial.

∑µ𝒊,𝒋 = 𝟏,∀𝒋 ∈ {𝟏, 𝟐, 𝟑, … . . , 𝒏}|𝑫𝑰| 𝒊=𝟏(3)

In Equation 4, it is ensured that the sum of the degree of membership values of each source node which comes under it’s vicinity (irange)with respect to each domain initial is always non-zero. This constraint guarantees that each domain initial has an expected assigned load from each source node in the network, preventing any null assignments.

∑µ𝒊,𝒋𝒏𝒊=𝟏> 𝟎,∀𝒋 ∈ {𝟏, 𝟐, 𝟑 … . , |𝑫𝑰|}, ∃ 𝒋 ∶ 𝒅(𝒊 ,𝒋) ≤ 𝒊𝒓𝒂𝒏𝒈𝒆 (4)

In this section, a concise description of the proposed partitioning algorithm for wireless sensor networks is provided. Once the domain initials (DIs) have been established, the subsequent step involves allocating the remaining nodes to their corresponding domain initials (DIi).

4.2. Problem Statement

Clustering of the wireless sensor network into disjoint and equally loaded appropriate number of
domains.
Given:

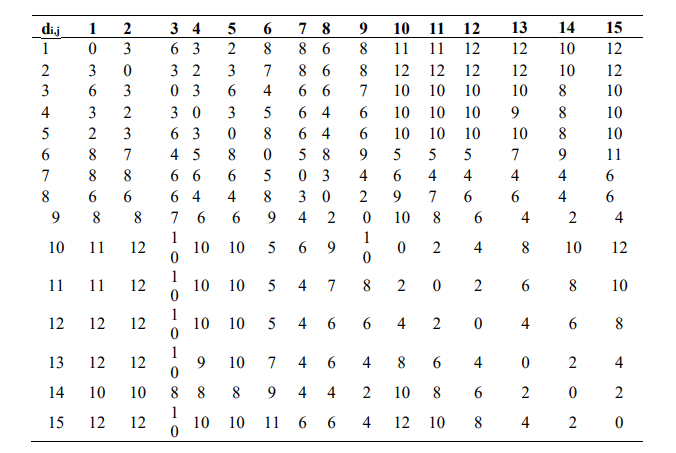
1. SN = {SN∈ i = 1, 2,….., n} – Documented set of n sensor nodes.
2. D = {dij, where, i∈ 1 to n; j ∈1 to n; i ≠ j} – Given by Table 2: Spatial distance of each
sensor node in illustrated wireless sensor network, where dij is the Euclidean distance,
described as the whole number.
3. The transmission range of each sensor node is taken as 5.

To find out:

Exhaustive partition of a set of source nodes (SN) into c number of domains.

Steps for proposed AFCM algorithm

1. Given: Set of n number of sensor nodes. SN = {1, 2, 3, …….n};
2. N = {SN– x: x is any centrally located node in the network};/*set of nodes that are to be
associated with the domains. This set contains all sensor nodes except the processing
element.
3. Set Level=0; Choose Llevel = {i: d ( PE, i) ≤ PErange;/* MA will be dispatched by PE by
choosing the nodes which directly come under PE’s vicinity. These nodes are termed
domain initials.
4. Update Nlevel = {N – Llevel};
5. Determine subsets of Llevel, DI = {∃𝑗 : d ( i, j) ≤ jrange: ∀ i∈ Nlevel,∀ j ∈Llevel;/* Set of
domain initials to which source node may be connected.
6. NDA = {∃ i ∈ Nlevel, : d ( i, j ) >jrange,∀j ∈Llevel}; /* Set of nodes i∈ N, which are not
directly connected to Llevel.
If ( NDA ≠ ∅ ) then
Nlevel = Nlevel – NDA;
7. Find µ𝑖,𝑗 =𝑑𝑖,𝑗−2𝑚−1∑ 𝑑𝑖,𝑗−2𝑚−1|𝐷𝐼|𝑙=1 ∀𝑖 ∈Nlevelw.r.t. each DI such that d (i, j) ≤ irange∀𝑖 ∈ Nlevel,∀𝑗 ∈
Llevel;
8. Calculate the estimated load of each DI by adding µ values of each DI w.r.t. nodes thatcome under their vicinity;
9. Associate the nodes with the DIi
10. If (NDA ≠ ∅) then
i) Llevel = Nlevel,
ii) Level = Level +1,
iii) Nlevel= NDA,
iv) Go to step 5 and repeat until NDA = ∅;
11. Check if there is any domain having data to be carried by the mobile agent less than the
MA’s threshold value then less loaded domain needs to be dropped out by following step
11 else go to step 13;

12.Identify each node of this domain (to be dropped out) with their corresponding Llevel and
assign identified nodes to their respective same level by considering membership values;
13. Stop;

In some domains, the amount of data that needs to be carried by the Mobile Agent (MA) associated with the domain’s nodes may be less than the MA’s threshold value. The threshold value represents the minimum data quantity for which a dedicated MA should be deployed. In such cases, these domains should be excluded or dropped out. Consequently, all relevant nodes will be associated with their respective domain, denoted by j∈Li, where the membership degree (µ) is maximum. Similarly, the remaining nodes that were previously associated with the dropped domain (j) should be connected to the remaining domains (j).

4.3. Evaluating Efficiency of Fuzzy-Based Clustering Algorithm for Wireless Sensor Network Partitioning: An Illustrative Example

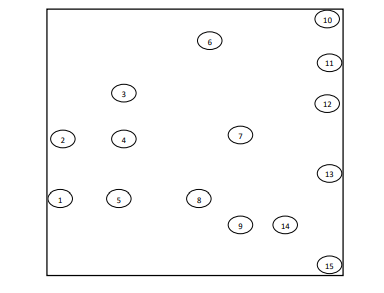
In Figure 1, a specific instance of a wireless sensor network comprising 15 nodes is depicted. The
figure also demonstrates the spatial separation between nodes within the network.

Figure 1: Representation of a Wireless Sensor Network with 15 Nodes

The Fuzzy C-means (FCM) clustering algorithm, initially applied to wired networks as detailed in [44], is here re-examined in the context of wireless sensor networks (WSNs) using the same illustrative network. This study shifts focus to explore fuzzy-based clustering in WSNs, as presented in Table 5, which outlines the range matrix for the discussed network. The objective is to demonstrate the algorithm’s effectiveness in partitioning both wired and wireless networks while ensuring that clusters maintain non-overlapping domains. The research highlights the significant differences between clustering wired and wireless networks due to their distinct characteristics: wired networks have fixed, stable topologies that optimize static connections, whereas WSNs feature dynamic, irregular topologies with mobile nodes, necessitating adaptable clustering strategies to address issues such as energy constraints and communication variability. By comparing clustering outcomes in WSNs with those from wired networks, this study emphasizes the need for tailored approaches that effectively manage the unique challenges of each network type.

The distinction between applying the proposed clustering algorithm to wired versus wireless networks lies in how proximity is considered. In wireless networks, clusters are formed based on the wireless range between the processing elements and the centroids of the nodes selected for clustering. This approach accounts for the variable communication range and signal strength inherent to wireless environments. In contrast, in wired networks, clustering is based on the physical proximity of nodes to each other rather than their proximity to a centroid. This reflects the fixed and stable nature of wired connections, where mutual proximity is the primary factor in cluster formation. The application of the proposed algorithm is illustrated as follows:

Table 5: Spatial distance of each sensor node in wireless sensor network[39]

Node 8, selected as the Processing Node (PE) due to its central location, serves as the basis for the proposed fuzzy-based clustering algorithm. With the chosen PE, nodes 4, 5, 7, 9, and 14 will be grouped together as elements of the set DI. Table 6 provides a list of domains to which each source node may be connected. However, node 10 does not have any domain (DIi) within its transmission range. Therefore, node 10 will be categorized as a member of the set NDA (Not Directly Associated) in this context.Table 7presents the degree of membership (belongingness) of each source node (SNi) to its corresponding Domain Initial (DI).

Table 6: : Set of domain initials to which node may be connected

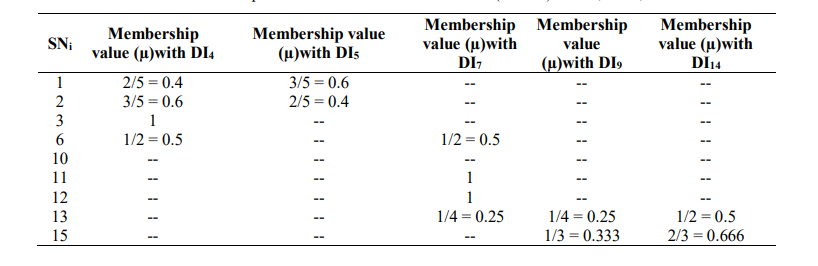
Table 7: Membership values (µ) of each sensor node for the current set of domain initials

In this scenario, the expected assigned load for each domain initial can be calculated by summing the membership values of each domain initial with respect to each sensor node. For the given example, the expected assigned load for domain initials 4, 5, 7, 9, and 14 are 2.5, 1, 2.75, 0.583, and 1.166, respectively.

Table 8: Association of succeeding sensor nodes to their respective domain initial

Table 8 presents the nodes in ascending order of the cardinality of set DI (as shown in Table 6), ensuring that nodes with smaller cardinality sets are associated first. In the assignment process, each node is associated with the DIi that has the highest membership value, as indicated in Table 7. However, if multiple DIi have the same membership value for a node, the node is connected to the DIi with the lower assigned load. This approach ensures that all nodes within the vicinity of DIi are appropriately associated.

In contrast, the set NDA contains one element, node 10, which needs to be connected to the source nodes that are already linked to DI in the previous iteration. In this iteration, the elements of set DI are replaced by the elements of set N, i.e., 1, 2, 3, 6, 11, 12, 13, and 15, while the elements of set N are replaced by the element of set NDA, which is 10. Table 9 displays the degree of belongingness of node 10 with respect to the new set DI.

Table 9: Membership values (µ) of the set NDA for the new set DI

• In this paper, the modification of the proposed algorithm produced three distinct
  • domains: {1, 2, 3, 4, 6}, {7, 10, 11, 12}, and {5, 9, 13, 14, 15}, with node 8 chosen as the Processing Element.
• In contrast, applying the FCM algorithm to general/wired networks, as described in [46],
  • resulted in a different partitioning of the instance network into three domains: {1, 2, 3, 4,5}, {6, 7, 10, 11, 12}, and {9, 13, 14, 15}.
• Both networks were structured with an equal number of domains and an identical numberof nodes per domain, though the specific nodes within each domain varied.
• The loads for the wired networks were determined as minL(wired), minL(wired) + 0.2,and minL(wired) + 0.4, where minL(wired) represents the minimum load.
• The loads for the wireless networks were minL(wireless), minL(wireless) + 0.374, andminL(wireless) + 0.306, with the minimum load for wireless networks denoted as minL(wireless).
• In both cases, the domains maintained the same cardinality of 4, 5, and 5 nodes; however,the composition of nodes within each cluster differed between the two algorithms.

6. CONCLUSION

The research paper introduces the Adaptive Fuzzy c-Means (AFCM) algorithm to address the limitations of existing clustering methods like k-means, x-means, and Fuzzy c-Means (FCM) in multi-mobile agent itinerary planning (MIP). The AFCM algorithm enhances network clustering by effectively managing sensor nodes with equal membership values and ensuring balanced, nonoverlapping domains. This improvement optimizes the efficiency of MIP systems, particularly under varying constraints. The algorithm demonstrated success in partitioning networks into well-balanced domains and suggested an appropriate number of mobile agents for optimized performance.

Future research can be focused on exploring the AFCM algorithm’s performance under diverse network constraints and in larger-scale systems. Additionally, integrating AFCM with real-world MIP applications could further validate its effectiveness and scalability.

Compliance with Ethical Standards

The authors have no conflicts of interest to declare. All the co-authors have seen and agree with the contents of the manuscript and there is no financial interest to report.  Each author have made substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data.

 

REFERENCES

[1] E. Fissaoui, M. Beni-hssane and S. A. Ouhmad, “A survey on mobile agent itinerary planning for information fusion in wireless sensor networks,” Archives of computational methods in engineering, vol. 28, pp. 1323-1334., 2021.
[2] S. Khan, A. Tariq, H. Richard and A. A. Hussain, “Multi-Mobile Agent Security by Design Itinerary Planning Approach in Wireless Sensor Network,” in International Conference on Ubiquitous Security (pp. 534-544).:Springer Nature S, Singapore, December, 2022.
[3] Chen, M., Cai, W., Gonzalez, S., & Leung, V. C., “Balanced itinerary planning for multiple mobile agents in wireless sensor networks,” in International conference on ad hoc networks., Berlin, Heidelberg, 2010.
[4] Chou, Y. C., & Nakajima, M., “A clonal selection algorithm for energy-efficient mobile agent itinerary planning in wireless sensor networks,” Mobile Networks and Applications, vol. 23, no. 5, pp. 1233-1246, 2018.
[5] Hong, W., Liu, Z., Chen, Y., & Guo, W., “Energy-efficient mobile agent communications for maximizing lifetime of wireless sensor networks,” in Wireless Communications, Networking and Applications, New Delhi, 2016.
[6] S. P. Ardakani, “Data aggregation routing protocols in wireless sensor networks: A taxonomy,” International Journal of Computer Networks & Communications, vol. 9, no. 2, 2017.
[7] S. P and S. R., “Invesigation of Ant Colony Optimization Algorithm for Efficient Energy Utilization in Wireless Sensor Network,” International Journal of Computer Networks & Communications, vol. 15, no. 4, 2023.
[8] Chen, Min, et al., “Mobile agent-based directed diffusion in wireless sensor networks,” EURASIP Journal on Advances in Signal Processing, pp. 1-13, 2006.
[9] Lingaraj, K., Biradar, R. V., & Patil, V. C., “Eagilla: An enhanced mobile agent middleware for wireless sensor networks,” Alexandria engineering journal, vol. 57, no. 3, pp. 1197-1204, 2018.
[10] M. M. Islam and J. Fariha Tasmin, “MAXIMIZING NETWORK INTERRUPTION IN WIRELESS SENSOR NETWORK: AN INTRUDER’S PERSPECTIVE,” International Journal of Computer Networks & Communications, vol. 7, no. 2, p. 103, 2015.
[11] V. N and S. J. M, “INTELLIGENT EFFICIENT ROUTING AND LOCALIZATION IN THE UNDERWATER WIRELESS SENSOR NETWORK TO IMPROVE NETWORK LIFETIME,”
[12] Konstantopoulos, C., Mpitziopoulos, A., Gavalas, D., & Pantziou, G., “Effective determination of mobile agent itineraries for data aggregation on sensor networks,” in IEEE transactions on knowledge and data engineering, 2009.
[13] Nidhi, Shuchita Upadhyaya, “A Comparative Analysis of Itinerary Planning Algorithms for Single Mobile Agent and Multi Mobile Agent,” International Journal of Computer Sciences and Engineering, vol. 6(3), pp. 92-96, 2018.
[14] N. Souparnika Jadhav and Nagesh K. N, “Energy Harvesting Rectenna Design for Enhanced Node Lifetime in WSNs,” International Journal of Computer Networks & Communications, vol. 14, no. 2,
2023.
[15] N. Kashyap, S. Upadhyaya, M. Poriye, S. Laler and S. Aggarwal, “Assessing the efficacy of a novel adaptive fuzzy c-means (AFCM) based clustering algorithm for mobile agent itinerary planning in wireless sensor networks using validity indices.,” Peer-to-Peer Networking and Applications, pp. 1- 13, 2024.
[16] T. Alsboui, Q. Yongrui, H. Richard and A. A. Hussain, “An energy efficient multi-mobile agent itinerary planning approach in wireless sensor networks,” Computing, vol. 103, no. 9, pp. 2093- 2113, 2021.
[17] S. Chaudhary, K. U. and G. S., “Energy-efficient and secured mobile agent itinerary approach in wireless sensor network.,” in In Innovations in Electrical and Electronic Engineering: Proceedings of ICEEE 2020 (pp. 693-711). Springer, Singapore., 2021.
[18] O. S. Egwuche, S. A. Olumide, A. O. Samuel and A. D. Oladunni, “Enhancing network life-time of wireless sensor networks through itinerary definition and mobile agents for routing among sensor nodes.,” in International conference in mathematics, computer engineering and computer science (ICMCECS) (pp. 1-7)., March, 2020.
[19] Aloui, I., Kazar, O., Kahloul, L., & Servigne, S., “A new itinerary planning approach among multiple mobile agents in wireless sensor networks (WSN) to reduce energy consumption,” International Journal of Communication Networks and Information Security (IJCNIS), vol. 7, no. 2, p. 116, 2015.
[20] Aloui, I., Kazar, O., Kahloul, L., Aissaoui, A., & Servigne, S., “A new” data size” based algorithm for itinerary planning among mobile agents in wireless sensor networks,” in In Proceedings of the International Conference on Big Data and Advanced Wireless Technologies, 2016.
[21] Qadori, H. Q., Zulkarnain, Z. A., Hanapi, Z. M., & Subramaniam, S., “A spawn mobile agent itinerary planning approach for energy-efficient data gathering in wireless sensor networks,” Sensors, vol. 17, no. 6, pp. 1280-1296, 2017.
[22] Daramola, O. A., Fakoya, J. T., Danjuma, H. I., & Egwuche, O. S., “Towards clustering technique for a fault tolerance mobile agent‐based system in wireless sensor networks,” Int J Comput Sci Inf Secur (IJCSIS), vol. 19(1), pp. 48-58, 2021.
[23] Ardakani, Pourroostaei, “MINDS: Mobile agent itinerary planning using named data networking in wireless sensor networks.,” Journal of Sensor and Actuator Networks, 10(2), 28., vol. 10, no. 2, 2021.
[24] Mpitziopoulos, A., Gavalas, D., Konstantopoulos, C., & Pantziou, G., “Deriving efficient mobile agent routes in wireless sensor networks with NOID algorithm,” in IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, 2007.
[25] Gavalas, D., Venetis, I. E., Konstantopoulos, C., & Pantziou, G., “Energy-efficient multiple itinerary planning for mobile agents-based data aggregation in WSNs,” Telecommunication Systems, vol. 63, no. 4, pp. 531-545, 2016.
[26] Liu, Bo; Jiuxin, Cao; Jie, Yin; Wei, Yu; Benyuan, Liu; Fu, Xinwen;, “Disjoint multi mobile agent itinerary planning for big data analytics,” Journal on Wireless Communications and Networking, vol. 2016, pp. 1-12, 2016.
[27] Mpitziopoulos, A., Gavalas, D., Konstantopoulos, C., & Pantziou, G., “CBID: a scalable method for distributed data aggregation in WSNs,” International Journal of Distributed Sensor Networks, vol. 6(1), 2010.
[28] Gavalas, D., Pantziou, G., Konstantopoulos, C., & Mamalis, B., “New techniques for incremental data fusion in distributed sensor networks,” in Proceedings of the 11th Panhellenic Conference on Informatics (PCI’2007), 2007.
[29] Kuila, P., Gupta, S. K., & Jana, P. K., “A novel evolutionary approach for load balanced clustering problem for wireless sensor networks,” Swarm and Evolutionary Computation, vol. 12, pp. 48-56, 2013.
[30] Wu, Q., Rao, N. S., Barhen, J., Iyenger, S. S., Vaishnavi, V. K., Qi, H., & Chakrabarty, K., “On computing mobile agent routes for data fusion in distributed sensor networks.,” in IEEE Transactions on Knowledge and Data Engineering, 2004.
[31] Rajagopalan, R., Mohan, C. K., Varshney, P., & Mehrotra, K., “Multi-objective mobile agent routing in wireless sensor networks,” in IEEE Congress on Evolutionary Computation, 2005.
[32] Cai, W., Chen, M., Hara, T., Shu, L., & Kwon, T., “A genetic algorithm approach to multi-agent itinerary planning in wireless sensor networks,” Mobile Networks and Applications, vol. 16, no. 6, pp. 782-793, 2011.
[33] Chen, M., Gonzalez, S., Zhang, Y., & Leung, V. C., “Multi-agent itinerary planning for wireless sensor networks,” in International Conference on Heterogeneous Networking for Quality, Reliability, Security and Robustness, Berlin, Heidelberg, 2009.
[34] Wang, J., Zhang, Y., Cheng, Z., & Zhu, X., “EMIP: energy-efficient itinerary planning for multiple mobile agents in wireless sensor network,” Telecommunication Systems, vol. 62, no. 1, pp. 93-100, 2016.
[35] Lingaraj, K., Biradar, R. V., & Patil, V. C. (2017)., “OMMIP: An optimized multiple mobile agents itinerary planning for wireless sensor networks,” Journal of Information and Optimization Sciences, vol. 38(6), pp. 1067-1076, 2017.
[36] El Fissaoui, M., Beni-Hssane, A., & Saadi, M. (2018). Multi-mobile agent itinerary planning-based energy and fault aware data aggregation in wireless sensor networks., EURASIP Journal on Wireless Communications and Networking, vol. 1, pp. 1-11, 2018.

[37] Chen, M., Gonzalez-Valenzuela, S., & Leung, V. C., “Directional source grouping for multi-agent itinerary planning in wireless sensor networks,” in International conference on information and communication technology convergence (ICTC), 2012.
[38] Bendjima, M., Feham, M., & Lehsaini, M., “Directional Itinerary Planning for Multiple Mobile Agents in Wireless Sensor Networks,” Wireless Communications and Mobile Computing, 2021.
[39] Cai, Wei, Min Chen, and Xiaofei Wang., “Angle gap (AG) based grouping algorithm for multimobile agents itinerary planning in wireless sensor networks.,” 2009.
[40] Gupta, G. P., Misra, M., & Garg, K., “Towards scalable and load-balanced mobile agents-based data aggregation for wireless sensor networks,” Computers & Electrical Engineering, vol. 64, pp. 262- 276, 2017.
[41] Karthik, S., Karthick, M., Karthikeyan, N., & Kannan, S., “A multi-Mobile Agent and optimal itinerary planning-based data aggregation in Wireless Sensor Networks,” Computer Communications, vol. 184, pp. 24-35, 2022.
[42] R. &. S. V. Saravanan, “Wireless sensor network data gathering using a multi-fold gravitational search algorithm with a mobile agent.,” International Journal of System of Systems Engineering, vol. 14, no. 1, pp. 23-41., 2024.
[43] Yousefi, S., Derakhshan, F., Karimipour, H., & Aghdasi, H. S., “An efficient route planning model for mobile agents on the internet of things using Markov decision process,” Ad Hoc Networks, vol. 98, 2020.
[44] Nidhi, Shuchita Upadhyaya, “Fuzzy C-Means Clustering of Network for Multi Mobile Agent Itinerary Planning,” in Smart Trends in Computing and Communications, vol. 396, Warsaw, Poland, Springer, 2022, pp. 589-598.