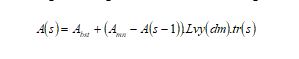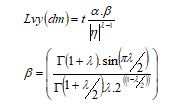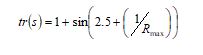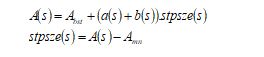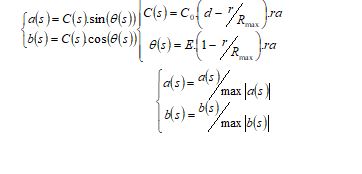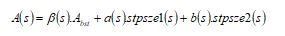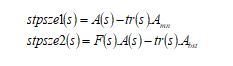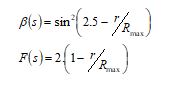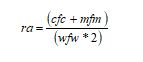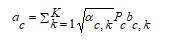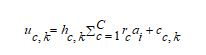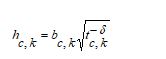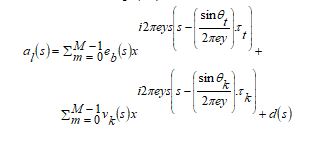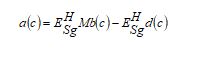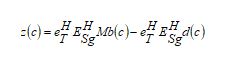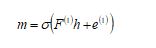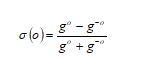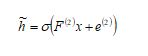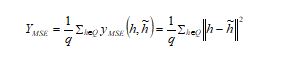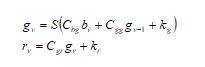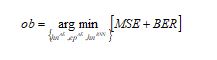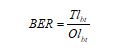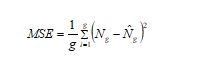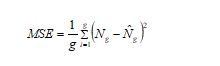IJCNC 07

Adaptive Hybrid Deep Learning based Effective Channel Estimation in MIMO-NOMA for Millimeter-Wave Systems with an Enhanced Optimization Algorithm

Belcy D Mathews  and Tamilarasi Muthu

Department of Electronics and Communication Engineering, Puducherry Technological University, Puducherry, India

Abstract

The channel estimation is crucial in the “millimeter Wave (mmWave) Massive Multiple-Input Multiple Output (MIMO) and Non-Orthogonal Multiple Access (NOMA)” devices. Hybrid beamforming techniques are employed nowadays to minimize the complexity and equipment price. However, the absence of digital beam forming in mmWave affects the dynamic range and accuracy of the channel estimation. Previous research has concentrated mainly on predicting narrow-band mmWave channels using deep learning networks, as the wideband channels of mmWave create a considerable range and noise issue. Accurate channel estimation in the MIMO system is challenging because of the increased number of antennas and radio frequency (RF) chains. MIMO system communications using mmWave are frequently chosen because of their massive spectrum resources. Therefore, it is essential to tackle the obstacles obtained in the standard channel estimation framework by developing a MIMO-NOMA network with the help of deep learning methods Hence, this paper proposes an efficient hybrid deep learning model for channel estimation in MIMO-NOMA for mmWave systems. At first, the channel estimation is carried out using the Adaptive Hybrid Deep Learning (AHDL) model, where it combines both Autoencoder and Recurrent Neural Network (RNN). Here, the parameters are optimized using the Improved Red-tailed Hawk Algorithm (IRHA). Later the hardware cost and system complexity are reduced by performing the hybrid beam-forming process. Numerical results show that the proposed channel estimation and pilot estimation process outperforms the state-of-the-art approaches

KEYWORDS

Multiple-input multiple-output; Non-Orthogonal Multiple Access; Channel Estimation; Adaptive Hybrid Deep learning; Improved Red-tailed Hawk Algorithm

1. Introduction

Nowadays, mmWave communication devices have developed as an effective innovation for the future generation of wireless communications [1]. The mmWave utilizes high-frequency bands of mmWave, where the spectrum is underused and less crowded. The NOMA is a significant principle for future networks and radio access in 5G [2]. NOMA is on the basis of the concept that numerous candidates are multiplexed against the same orthogonal resource module [3]. Nowadays, the NOMA has been suggested as an effective access mechanism that can fulfill the present 5G and beyond requirements including high connection density, improved user coverage, and low latency [4]. The significance of the NOMA is to assign the non-orthogonal resources to assist the numerous candidates providing better spectral effectiveness while having minimum disturbance at the receivers [5]. Though there is a large amount of spectrum present in the mmWave band, the utilization of NOMA in the mmWave band is significant because of the mass connectivity of the NOMA with the mmWave network, higher spectral efficacy, and also less delay [6]. Precise CSI is significant to attain the overall merits of mmWave with NOMA innovation. But, the most complex task is to achieve precise CSI [7].

The combination of MIMO and NOMA has been experimented with conventional communication standards [8]. The conventional standards employed the beamforming model that reduces the transmission power [9]. Moreover, in conventional works, an efficient transmission approach is implemented that confirms the network coverage in that multi-antenna BS that sends various individual antenna elements employing NOMA [10]. It is significant to employ the NOMA in mmWave because of the numerous merits including the channels of distinct users in the same way are highly correlated in the mmWave [11]. This unique channel feature of mmWave is highly applicable to utilizing the NOMA. Moreover, the wide-scale antenna array offers very effective directional beams in the mmWave [12]. This provides better beamforming gains and lower interferences, where the transmissions of NOMA are given to each beam [13]. The overload of the user is enhanced by employing NOMA in mmWave transmission enhances the spectral efficiency.

Compressive sensing (CS) is an effective field to regenerate the sparse physical signal from the pending sequential model of derivations [14]. In the past years, numerous CS-aided models have been employed for NOMA devices by employing various sparsity frameworks [15]. However, these models consider that the channels for overall candidates are referred a priori which is not highly practical. This is because of the truth that numerous candidates are idle and the CSI is outdated [16]. Deep learning has attained enhancing popularity in the modern days. Deep learning is a data-driven technique, where the frameworks are implemented over a huge amount of data sources and an effectively trained mathematical system is not necessary [17]. These attributes are a result of employing deep learning in the transmission model. A learned denoising-aware approximate message-transmitting model is employed to determine the channel for the MIMO model. The traditional channel estimation technique has a tractable technique. However, the practical channel estimation can be ineffective and highly complex.

The contributions of the designed channel estimation framework are listed below.

• To present a new channel estimation framework in MIMO-NOMA for the mmWave system by utilizing the deep learning method that minimizes the interferences and error rates of the network. Moreover, it improves the data transmission rates and signal connectivity.
• To present an AHDL network by integrating the autoencoder and RNN techniques that effectively perform the channel estimation in MIMO-NOMA. Here, the IRHA is also applied for optimally determining the AHDL network’s parameters. This AHDL-based channel estimation framework optimizes the data transmission by offering significant data.
• To recommend an IRHA model by utilizing the necessary features of the existing RHA that supports the channel estimation framework with its higher convergence rates and capacity to choose the optimal solutions. Moreover, it fine-tunes the parameters such as epochs and hidden neuron counts in the designed AHDL network.

This paper is framed as follows. Part II illustrates the conventional channel estimation works in MIMO-NOMA. Part III demonstrates the basic model of MIMO-NOMA with mm-wave system and problems related to channel estimation. Part IV explains the description of IRHA for parameter optimization. Part V offers the channel estimation employing the AHDL model and its fitness formulation. Part VI displays the research findings of the designed channel estimation framework. Part VII provides the conclusion of the recommended channel estimation framework.

2. Existing Works

2.1.1.  Related Works

In 2021, Pawar et al. [18] offered a max-min power control factor that increased the low noise achievable value. In addition, the authors examined two distinct grouping mechanisms and analyzed their impacts on this noise achievable rate. The authors validated the functionality attained by the highest ratio decoder. The simulations and the extensive evaluations display that the developed model provided a high max-min achievable value between the overall considered grouping and decoding mechanisms.

In 2023, Ahmad et al. [19] have introduced the channel estimation of the massive MIMO NOMA models and the identification technique that employed deep learning to mitigate the problems of erroneous signal identification created by the imperfect CSI. The experiment displayed that the deep learning-aided estimation of the channel and the identification technique canceled the interference more effectively than the traditional channel estimation models. In addition, the wavelet-aided technique was compared to the conventional techniques. The simulation solutions displayed that the designed technique outperformed the existing techniques.

In 2023, Mathews and Tamilarasi [20] recommended a Black Window Optimization (BWO)-aided network to validate the channel for the mmWave-MIMO devices. The implemented model employed the hybrid beamforming mechanism to minimize the hardware complexity of the model and the hardware expenses of the MIMO system. The simulation experiments ensured that the implemented technique offered enhanced classification functionality and spectral efficiency when compared with the existing channel estimation approaches.

In 2019, Gao et al. [21] examined the issue of wideband beamspace channel validation without general support consideration. The authors initially confirmed that wideband beamspace’s path factor offered a special frequency-relied sparse framework by utilizing the beam squint’s effect. The author’s method effectively validated the overall sparse path factors following the conventional concept of interference mitigation. The experimental outcomes revealed that the designed model minimized the pilot overhead and also obtained enhanced accuracy of the channel estimation.

In 2022, Audu and Oyerinde [22] employed a 3D geometric channel system to implement a very realistic technique for extra signal perturbations. The developed estimator named Singular Value Decomposition (SVD) focussed on tolerating the system burdens and minimizing the correctness of the channel estimation. The recommended system’s outcome displayed timely convergence during the research and scaled the complexity than the earlier developed techniques.

In 2024, Oyerinde et al. [23] aimed to develop a channel estimation technique with enhanced functionality in comparison with other traditional estimation models. The developed channel estimation framework utilized the hybrid mechanism to integrate the enhanced Compressive Sensing Algorithm (CSA). The recommended estimator displayed enhanced functionality when contrasted with the other conventional channel estimators.

In 2024, Van [24] examined the security and reliability of the “MIMO NOMA transmission with energy harvesting-aided full-duplex jammer (MMnOehFD)”, where numerous evaluation factors were considered. In addition, the practical attributes were also utilized in this validation. The designed model could prevent the overall outage and achieve optimal functionality with a specific configuration of the device. The functionality of the model was enhanced with an enhanced amount of antennas. In addition, the model performed better than the conventional techniques.

In 2024, Chandra and Borugadda [25] considered the integrated framework uplink communication for the MIMO NOMA model’s power effectiveness and beam forming enhancement via three-layer candidate grouping. In this grouping process, the K-means algorithm was employed in the starting layer for grouping the candidates and minimizing the clustering faults in the 3rd layer. The 2nd layer was employed for integrating the small clusters. The beam selection was performed to reduce the intrusion. The solutions displayed that the implemented technique provided a better sum rate.

2.2 Research Gaps and Challenge

NOMA techniques are being developed to mitigate several primary limitations in future wireless transmissions. Especially, the channel estimation is highly complex where the NOMA techniques are combined with the mmwave massive MIMO. A precise channel estimation is crucial in utilizing the merits of connecting mmWave and NOMA. Various methodologies have been offered in the recent years. Nevertheless, these models need some improvements and some of the research experiments are explained below.

• The traditional channel estimation techniques are complex and have poor interpretability. Therefore, a simple channel estimation framework is necessary.
• The conventional deep learning-aided channel estimation models utilize only one optimization technique. These techniques are prone to error and ignore the significant features. Therefore, a hybrid deep learning model is significant for performing the channel estimation.
• Some of the existing channel estimation models are not suitable for practical use. Therefore, a suitable and efficient channel estimation model is necessary for MIMO-NOMA.
• The traditional channel estimation models utilize more processing time and encounter overfitting issues. Hence, optimizing the channel estimation models is necessary with the support of optimization algorithms.
• Some other classical models could not process the vast amount of data and were also sensitive to noise. To rectify these difficulties, a new technique is important.

Hence, an effective channel estimation system is implemented in this work for MIMO-NOMA using deep learning.

3. Basic Model of MIMO-NOMA with mm-Wave System and Problem-Related to Channel Estimation

3.1  MIMO-NOMA: System View

MIMO is a wireless antenna innovation that employs numerous antennas at both receiver and transmitter to enhance wireless communication efficiency. The MIMO model can improve the data throughput by sending numerous data streams continuously. The signal quality is also improved by the MIMO which minimizes the interference and fading effects. The MIMO can increase the wireless communication’s range by enhancing the signal-to-noise ratio (SNR) at the receiver. The MIMO-NOMA is a mechanism that integrates the merits of MIMO and NOMA. It enables numerous users to send and obtain data continuously employing numerous antennas, and improved signal processing mechanisms. In the implemented channel estimation framework, the input data is forwarded to the data converter. Here, the input data stream is converted into parallel information. Further, the obtained parallel information is provided to the 64-QAM model that utilizes the individual radio wave to indicate the six bits of achieved parallel information. With the subcarrier module, the modulator is connected to generate the pilot modules. In this, the signals are transformed to the time sector by employing the mechanism named Inverse Fast Fourier Transform (IFFT). Additionally, in the dispute multipath fading, the Cyclic Prefix (CP) is included. In this, the multipath fading’s length increases the channel’s largest latency speed. An effective IRHA is utilized to optimize the pilot symbol supports to improve the estimation efficiency of the channel. The channel estimation is conducted on the designed AHDL technique by considering the channel matrix. The primary objective of the channel estimation is to minimize the MIMO-NOMA system’s error rate by optimizing the parameters employing IRHA.

3.2. Motivation for Channel Estimation 

Channel estimation [27] is the operation of validating the features of the wireless channel between the receiver and transmitter including interference, delay, fading, and path loss. The channel estimation is necessary for developing and tuning the wireless transmission devices. However, channel estimation encounters numerous difficulties in dynamic environments, where the conditions of the channel quickly vary because of the environment, traffic, and mobility attributes. Some of the limitations and motivations in the channel estimation are given as follows. 

• Time-varying channel: One of the primary complexities in dynamic environments is the channel’s time-varying nature. The channel is not static, yet the variations over time are because of the transmitter motions, objects, or receivers in the environment. This creates the channel to face delay spread, multipath fading, and Doppler shifts that impact the data rate and the signal quality. To mitigate this issue, the wireless systems require accurate and frequent channel estimation.

• Spatial diversity: The channel is not uniform, yet changes across distinct directions and regions. This creases the channel to face the angular spread, shadowing, and spatial fading that impact the interference level and the signal strength. To utilize the channel’s spatial diversity, the wireless devices require employing numerous antennas or relaying mechanisms that improve the coverage and signal quality. But, these strategies also improve the overhead and difficulty of the channel validation.

• Channel estimation techniques: The channel is not simple to validate as it includes resolving difficult mathematical issues. There are numerous channel estimation modes, which have been divided into distinct types. Each type has its own limitations, merits, and assumptions concerning adaptability, robustness, complexity, and so on. Hence, selecting a suitable channel estimation model is important for satisfying the user requirements.

• Channel model: There is no single channel design that has the capacity to capture overall variations and the features of the channel in dynamic environments. Hence, the systems require employing distinct channel models for distinct applications and scenarios. In addition, the systems require estimating and validating their channel designs periodically which demands more data evaluation and collection.

• Non-linear distortion: The channel is not linear and utilizes non-linear impacts including clipping, harmonic distortion, and inter-modulation that affect the spectral efficiency and the signal integrity. To reduce this problem, wireless systems require employing improved signal processing models. But these models also demand more robust and accurate channel estimation.

3.3 Proposed CE Technique

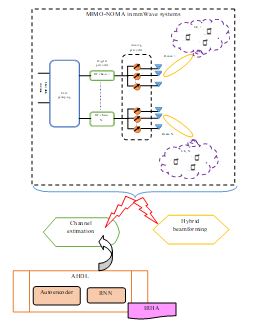
With an increased requirement for radio spectrum resources, the underused mmWave band has attained wide attention because of its higher spectral efficiency and large bandwidth. Since the transceiver compensates for the greater loss of propagation employing the beam gain provided by the wide-scale antenna array, the mmWave integrated with the wide-scale antenna array becomes the fundamental supporting innovation in the 5G transmission devices. The combination of NOMA and the MIMO has been analyzed in numerous works in the past years. But, these MIMO-NOMA approaches are all concentrated on low frequency and cannot be employed for the mmWave transmission, where the sparsity of the channel, number of conflicting user uncertainty, and so on also require to be focus. It is understood that the overall merits of the mmWave with the NOMA innovation relatively depend on the accurate CSI validation that is also considered as one primary complexity for mmWave NOMA devices. Some of the channel validation approaches for the mmWave device have been recommended on the basis of numerous traditional models. However, the traditional channel estimation models are highly on the basis of an on-grid mechanism that is always troubled by functionality loss because of energy leakage. Hence, some experts implemented off-grid channel estimation techniques. However, conventional techniques face limitations including complex signal processing. Hence, an effective channel validation framework is necessary for the MIMO-NOMA in the mmWave system. Figure 1 displays the functional diagram of the implemented estimation of the channel system for the MIMO-NOMA in the mmWave system.

Figure 1. Functional diagram of proposed channel estimation framework for MIMO-NOMA in mmWave systemt

---

A hybrid deep learning framework is suggested in this work for channel estimation in MIMO-NOMA for the mm Wave system. Initially, the estimation of the channel is performed by employing the AHDL technique. The suggested AHDL mechanism is the combination of the autoencoder and RNN techniques. In this, the AHDL model’s parameters are optimally tuned by the IRHA technique. Further, the complexity and the hardware expenses are minimized by performing beamforming. In the end, the efficacy of the presented model is correlated with some other traditional methods to display its superiority over others.

1. Improved Red-Tailed Hawk Algorithm for Parameter Optimization and Hybrid Beamforming Technique

4.1. Red-Tailed Hawk Algorithm

The existing RHA [26] is a meta-heuristic approach motivated by the bird named red-tailed hawk. The RHA utilizes the hunting mechanism of the red-tailed hawk and it follows three primary phases.

High soaring: The mathematical stage of this phase is shown in Eq. (1).

Here, the region of the red-tailed hawk at the iteration is given as As The achieved best region is taken as Abst and the mean region is considered as Amn. The function of levy flight distribution is represented as L_vy that is estimated based on Eq. (2). Further, the transition factor is indicated astr s that is determined based on Eq. (3).

Here, the variable t is a fixed value (0.01), and the issue dimension is indicated as ‘dm’. The constant is taken as (1.5).

Here, the highest iteration is declared as R_max.

Low soaring: This phase is designed in Eq. (4).

Here, the direction coordinates are given as a and b, and these factors are estimated in Eq. (5).

Here, the radius’s starting value is given as C₀ in the range of [0.5-3], and the factor ‘E’ indicates the angle gain between 5 to 15. The control gain is denoted as ‘d’ from the range of [1, 2] and the updated arbitrary gain is denoted as ‘ra’.

Swooping and stopping: This phase is derived in Eq. (6).

Here, each step size is determined based on Eq. (7).

Here, the gravity and acceleration attributes are taken as ‘F’ and ‘β’ accordingly and these factors are determined in Eq. (8).

The acceleration of the hawk is given as ‘β’ enhanced with the improvement of ‘s’ to increase the speed of convergence. The variable ‘F’ is the gravity impact that minimizes to decreases the exploitation diversity. Algorithm 1 shows the pseudo-code of conventional RHA.

4.2. Improved Red-tailed Hawk Algorithm

The IRHA is designed to optimally determine the parameters in the AHDL model. The IRHA is improved from the existing RHA with an innovative mechanism. This IRHA helps to conduct the channel validation by optimizing the AHDL network parameters including epochs and hidden neurons. Thus, this method minimizes the “Bit Error Rate (BER) and Mean Square Error (MSE)” of the overall channel estimation process. As explained earlier, the IRHA is developed from the existing RHA. The RHA utilizes the hunting mechanism of the red-tailed hawk as an inspiration and solves complex optimization problems. Moreover, this algorithm provides higher performance with optimal solutions. However, the RHA includes the random gain in the phase named low soaring. This random gain ranges from 0 to 1. When the iteration count is high, the random gain factor demands more time to determine the better solutions. This negatively impacts the convergence and also leads to unsatisfactory solutions. Therefore, the IRHA is implemented, where the arbitrary gain is upgraded by the values of fitness. This helps to improve the convergence rates and offers satisfactory solutions. The improved random gain ‘ra’ is determined in Eq. (9). improved random gain is determined in Eq. (9).

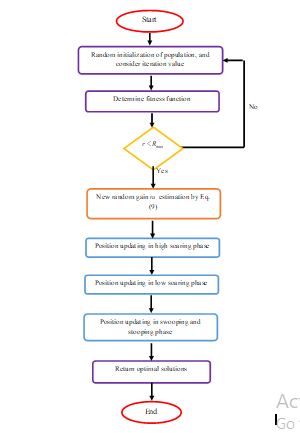
In this, the current fitness is taken as cfc, and the mean fitness is represented as mfm. Then, the worst fitness is considered as WFW. By the derived new arbitrary gain, Eq. (5) in the low soaring phase is modified and optimal solutions. The pseudo-code of recommended IRHA is given in Algorithm 2 and the flowchart of the presented IRHA is shown in Figure 2.

Figure 1Flowchart of IRHA

4.3. Hybrid Beamforming Model

Consider the MIMO-NOMA model in a macro cell with a 500m radius. The BS provides the power of transmission ‘P_wb’ and equally divides it among the antenna ‘C’. Hence, the superimposed signals are transmitted by the BS based on the NOMA attributes. Each User Equipment (UE) ‘M’ is randomly provided to the cells to produce the conditions of MIMO-

NOMA. In this, the power delivered through the individual antenna is specified as he nearby BS to the UE utilizes the SIC mechanism to prevent the interference signal in the MIMO-NOMA. The Rayleigh fading and the “Additive White Gaussian Noise (AWGN)” have an effect on the signals achieved from all UEs. The transmitted signal with the support of BS is formulated in Eq. (10).

(10)In this, the power transmitted attributes on each beam with candidates transferred signals, and the coefficient of power allocation is specified asand respectively. The obtained signals with the support of are given in Eq. (11).

In this, the factor of Rayleigh fading channel is indicated as that is determined among BS to, and the variable specifies the precoding vector. Then, the variable, and the attribute indicate the AWGN. Further, Eq. (12) offers the numerical form of.          

In this, the attribute points to the division among and BS. Eq. (13) gives the coefficient of power allocationon the basis of the NOMA principle.

In this, the attribute specifies the set of reliable power allocation variables. The end receiver includes of count of isotropic antenna factors that are partitioned into antenna arrays subgroups, where all subgroups have a number of antenna factors. The hybrid beamforming framework attains the required signal with as the “Angle Of Arrival (AOA)” and the number of interference signals with a changing AOA Here. The obtained sub-array signal in each antenna factor includes an AWGN signal, interference signal, and necessary narrow signal band. Hence, the obtained sub-array is formulated in Eq. (14).

Here, the variable specifies the distance between the nearby antenna array factors taken as.  The propagation delay of the required and interference signals is given as. The light intensity is specified as. According to the estimated baseband signal, each subset is validated in Eq. (15).

Here, the matrix diagonal is given as, and the variable indicates the analog beamforming stage’s input. The noise vector is specified as. While utilizing the digital beamforming factor to the digital beamforming state, Eq. (15) changes as given in Eq. (16).

The signal amplitude and the stage are distinguished by varying the digital beamforming attribute. Hybrid beamforming is employed in the technique for improving spectral effectiveness.

5. Channel estimation using an adaptive hybrid deep learning model

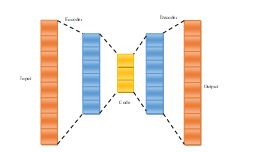
5.1. Autoencoder

The autoencoder [28] is a feed-forward neural network with three layers. It consists of a decoder and an encoder. The variable’s hidden representations are determined by the encoder with a sized vector as given in Eq. (17).

Here, the bias attribute and the weight matrix is specified as respectively. The activation function is pointed as. The hyperbolic tangent is estimated in Eq. (18) as it is utilized in this model.

The input vector is reconstructed by the decoder from the hidden vector to achieve the resultant vector as given in Eq. (19).

Here, the reproduced vector is considered as , and the bias vector is represented as. Further, the weight matrix is taken as.

The parameter validation of the autoencoder is conducted by reducing the following MSE regenerationconcerning the group of attributes utilizing the MSE as shown in Eq. (20)

The architecture of the autoencoder is provided in Figure 3.

Figure 1The architecture of the existing autoencoder model

5.2. Recurrent Neural Network

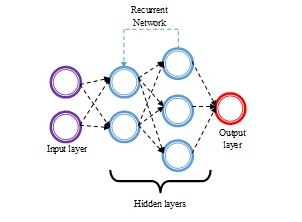
The RNN [29] is employed to forecast future data with the support of historical data samples. The RNN technique is very effective and utilized in implementing the sequence information. Moreover, the RNN method efficiently captures the long-term dependencies. The outcome of the RNN is determined by repeatedly executing Eq. (21) and Eq. (22) from.

Here, the resultant sequence is represented as , and the input is specified as. Then the weight matrix is specified as and the sequence of hidden vectors is pointed as. The hidden layer function is and the bias factor is. The diagrammatic illustration of RNN is given in Figure 4.

Figure 1RNN network

5.3. Proposed AHDL for Estimation

The AHDL technique is implemented for performing the channel validation in the MIMO-NOMA model. The AHDL model is a combination of autoencoder and RNN techniques. The autoencoder is highly effective for capturing significant features and showing accurate solutions. The RNN technique can improve the training efficiency and handle any length of input data. Though these techniques are effective, these techniques can’t offer satisfactory estimated solutions in terms of error rates and interference while processing individually. Hence, these two techniques are hybridized to offer the channel estimation properly. Thus, the HDL network is constructed for the developed model. However, when integrating the autoencoder, and RNN techniques causes overfitting troubles due to the high number of parameters such as epochs and hidden neurons in these models. To rectify this difficulty, the IRHA is utilized. This algorithm is suitable for choosing the optimal solutions and also has rapid convergence. Therefore, the IRHA is selected for this model. By utilizing the IRHA, the epochs and hidden neuron counts are optimally determined and its objective function is displayed in Eq. (23).    

        

In this, the autoencoder’s epoch count is pointed as varied from [5-255]. The autoencoder’s hidden neuron count is denoted as varied from [5-50]. Then, the RNN’s count of hidden neurons is given as varied from [5-255]. Further, the MSE and BER are minimized in this process. These measures are explained as follows.

BER: It is the bit count estimation, which is obtained in error contrasted to the total bits sent on the transmission technique. It is derived from Eq. (24).

Here, the overall bit count obtained with error is taken as, and the overall bit transformed in the network is given as.

MSE: It is the mean square variation between the actual and validated values. It is formulated in Eq. (25).

Here, the “predicted and actual” values are given as. The count of the data points is taken as.

AHDL: The channel matrix is provided as input for the AHDL mechanism, which is the integration of autoencoder, and RNN. The autoencoder and RNN techniques separately predicted the outcomes. Further, the predicted outcomes from both these techniques are averaged to obtain the effective channel estimated outcome. Thus, the AHDL technique helps to achieve the channel estimated solution for the MIMO-NOMA model. Figure 5 shows the pictorial illustration of AHDL for channel validation.

6. Results and Discussions

6.1. Simulation Setup

The developed channel estimation system was executed by the MATLAB 2020a platform. The implemented IRHA’s length of chromosome was 3 and the highest iteration was 50. The number of population of the IRHA was 10. Some of the existing models such as “DWT [2], BWO [3], CSA [6], and HDL [28] [29]” were utilized for the experiments. Moreover, several algorithms including “Clouded Leopard Optimization (CLO) [30], Wild Horse Optimization Algorithm (WHOA) [31], Coati Optimization Algorithm (COA) [32], and RHA [26]” were considered for the analysis. The parameter setting of the presented channel estimation framework is shown in Table 1.

Table 1. Parameter setting for the implemented Channel estimation Framework

Parameters	Values
Symbol’s time period	171ms
Small cell coverage	500 m
Carrier frequency	28 GHz
RF chains count	4
Channel Bandwidth	1 GHz
The number of BS antenna	64
Pilot count	200
CP Length	10 ms

6.2. Performance Evaluation of Developed Channel Estimation Framework based on SNR Values

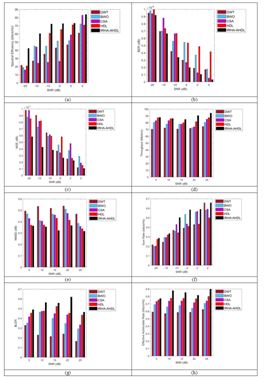
The designed channel estimation system’s performance is analyzed by utilizing the SNR values. This experiment is shown in Figure 6 over conventional related techniques. The developed channel estimation system’s MSE is decreased by 2.8% of DWT, 30% of BWO, 15.7% of CSA, and 11.4% of HDL appropriately when the SNR value is 5. This experiment explains that the implemented channel estimation model gives better outcomes than the existing techniques. Thus, it has been proved that the designed channel estimation system achieves more effective solutions than the classical models.

6.3. Performance evaluation of developed channel estimation framework based on user count

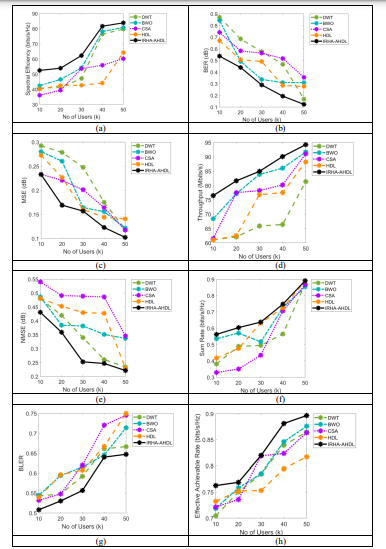
Figure 7 depicts the implemented channel estimation framework’s performance validation over traditional techniques using user counts. The throughput of the developed channel estimation model is enhanced by 24.24% of DWT, 7.27% of BWO, 6.66% of CSA, and 23.6% of HDL correspondingly for the 20th user count in Figure 7(d). Thus, it has been elaborated that the presented model offered more satisfactory solutions than the conventional models. Moreover, it has been explained that the implemented channel estimation framework minimizes the error values.

Figure 6Performance investigation of implemented channel estimation framework based on SNR values over conventional techniques in terms of “ (a) Spectral efficiency, (b) BER, (c) MSE, (d) Throughput, (e) NMSE, (f) Sum rate, (g) BLER, and (h) Effective achievable rat ;/p

Figure 7. . Performance investigation of implemented channel estimation framework based on user count over conventional techniques in terms of “ (a) Spectral efficiency, (b) BER, (c) MSE, (d) Throughput, (e) NMSE, (f) Sum rate, (g) BLER, and (h) Effective achievable rate”

7. Conclusions

This paper has explored the hybrid deep learning for performing the channel estimation in MIMO-NOMA for mmWave devices. In the very beginning, the channel estimation was conducted with the support of the AHDL mechanism. The recommended AHDL model was a combination of the existing RNN and autoencoder techniques. Here, the IRHA was exploited for optimally tuning the AHDL network parameters. Next, the complexity and the hardware expenses were reduced by conducting the beamforming task. Finally, the efficacy of the implemented model was contrasted with the existing models. The spectral efficiency of the designed channel estimation framework was enhanced by 2.5% of DWT, 1.25% of BWO, 35% of CSA, and 47.5% of HDL respectively when the user count was 40. From this research findings, it has been illustrated that the designed channel estimation system provided very low error rates and higher throughput than the traditional methods. In future work, the implemented channel estimation framework will be strengthened with other recent deep learning and optimization concepts for minimizing network interference.

REFERENCES

[1] Raveendran, T., “CNN based Channel Estimation using NOMA for mmWave Massive MIMO System”, arXiv preprint, 2021.
[2] Kanzariya, D., Trada, P., Kaswala, H. and Shah, H.B., “Deep Learning Based Signal Detection and Channel Estimation for MIMO-NOMA system”, Science, vol.1, pp.23-35, 2022.
[3] C. Hu, H. Wang, and R. Song, “Group Successive Interference Cancellation Assisted Semi-Blind Channel Estimation in Multi-Cell Massive MIMO-NOMA Systems,” IEEE Communications Letters, vol. 25, no. 9, pp. 3085-3089, Sept. 2021.
[4] M. H. Al-Ali and W. A. Al-Hussaibi, “Ergodic Sum Rate Expressions for Uplink MIMO-NOMA Under Spatial Correlation and Imperfect Channel Estimation,” IEEE Systems Journal, vol. 17, no. 4, pp. 5499-5510, Dec. 2023.
[5] Le-Thanh, T. and Ho-Van, K., “MIMO NOMA with nonlinear energy harvesting and imperfect channel information”, Arabian Journal for Science and Engineering, vol.49, pp.6675-6693, 2024.
[6] C. Hu, H. Wang, and R. Song, “Group Successive Interference Cancellation Assisted Semi-Blind Channel Estimation in Multi-Cell Massive MIMO-NOMA Systems,” IEEE Communications Letters, vol. 25, no. 9, pp. 3085-3089, Sept. 2021.
[7] M. H. Al-Ali and W. A. Al-Hussaibi, “Ergodic Sum Rate Expressions for Uplink MIMO-NOMA Under Spatial Correlation and Imperfect Channel Estimation,” IEEE Systems Journal, vol. 17, no. 4, pp. 5499-5510, Dec. 2023.
[8] Chen, S., Li, H., Zhang, L., Zhou, M. and Li, X., “Block sparse Bayesian learning based joint user activity detection and channel estimation in grant-free mimo-noma”, Drones, vol.7, no.27, 2022.
[9] Aldababsa, M. and Kucur, O., “Majority-based antenna selection schemes in downlink NOMA network with channel estimation errors and feedback delay”, IET Communications, vol.14, pp.2931- 2943, 2020.
[10] L. Wu, P. Sun, Z. Wang and Y. Yang, “Joint User Activity Identification and Channel Estimation for Grant-Free NOMA: A Spatial-Temporal Structure-Enhanced Approach,” IEEE Internet of Things Journal, vol. 8, no. 15, pp. 12339-12349, 1 Aug.1, 2021.
[11] Gollagi, S.G., Maheswari, S.S., Sapkale, P.V. and Poojitha, S., “Channel estimation for pilot contamination in massive MIMO-NOMA system”, Journal of High-Speed Networks, pp.1-19, 2024.
[12] H. Yu, Z. Fei, Z. Zheng, N. Ye, and Z. Han, “Deep Learning-Based User Activity Detection and Channel Estimation in Grant-Free NOMA,” IEEE Transactions on Wireless Communications, vol. 22, no. 4, pp. 2202-2214, April 2023.
[13] A. Salari, M. Shirvanimoghaddam, M. B. Shahab, R. Arablouei and S. Johnson, “Design and Analysis of Clustering-Based Joint Channel Estimation and Signal Detection for NOMA,” IEEE Transactions on Vehicular Technology, vol. 73, no. 2, pp. 2093-2108, Feb. 2024.
[14] Z. Wang, Z. Lin, T. Lv and W. Ni, “Energy-Efficient Resource Allocation in Massive MIMONOMA Networks With Wireless Power Transfer: A Distributed ADMM Approach,” IEEE Internet of Things Journal, vol. 8, no. 18, pp. 14232-14247, 15 Sept.15, 2021.

[15] Chung, K., “Impact of channel estimation errors on SIC performance of NOMA in 5G systems”, Journal of Convergence for Information Technology, vol.10, pp.22-27, 2020.
[16] Salari, A., Shirvanimoghaddam, M., Shahab, M.B., Arablouei, R. and Johnson, S., “Clusteringbased joint channel estimation and signal detection for NOMA”, arXiv, 2022.
[17] I. Khaled, C. Langlais, A. E. Falou, B. A. Elhassan and M. Jezequel, “Multi-User Angle-Domain MIMO NOMA System for mmWave Communications,” IEEE Access, vol. 9, pp. 129443-129459, 2021.
[18] A. R. Pawar, S. Kashyap and S. Chouhan, “Impact of Max-Min Power Control, Channel Estimation and User Grouping Strategies on Uplink Massive MIMO-NOMA Systems,” IEEE Transactions on Vehicular Technology, vol. 70, no. 8, pp. 7858-7869, Aug. 2021.
[19] Ahmad, M., and Shin, S.Y., “Wavelet-based massive MIMO-NOMA with advanced channel estimation and detection powered by deep learning”, Physical Communication, vol.61, no.102189, 2023.
[20] Mathews, B.D. and Tamilarasi, M., “Black Widow Optimization and Long Short-Term MemoryBased Channel Estimation in MIMO–NOMA for mmWave Systems”, Computational Electronics for Wireless Communications, pp. 169-179, 2023.
[21] X. Gao, L. Dai, S. Zhou, A. M. Sayeed, and L. Hanzo, “Wideband Beamspace Channel Estimation for Millimeter-Wave MIMO Systems Relying on Lens Antenna Arrays,” IEEE Transactions on Signal Processing, vol. 67, no. 18, pp. 4809-4824, 15 Sept.15, 2019.
[22] Audu, W.M. and Oyerinde, O.O., “Iteratively reweighted super-resolution channel estimation in hardware-impaired hybrid-precoded MM-wave massive MIMO systems using dual SVD and Marquardt’s global search”, Digital Signal Processing, vol.120, no.103308, 2022.
[23] Oyerinde, O.O., Flizikowski, A. and Marciniak, T., “Iterative hybrid compressive sensing-based channel estimation method for intelligent reflecting surface-supported millimeter wave systems”, AEU-International Journal of Electronics and Communications, no.155415, 2024.
[24] Ho-Van, K., “Secure MIMO NOMA transmission with energy harvesting-aided full-duplex jammer under erroneous channel information”, Digital Signal Processing, vol.151, no.104532, 2024.
[25] Chandra, K.R. and Borugadda, S., “Energy efficiency enhancement in millimeter-wave MIMONOMA using three layer user grouping and adaptive power allocation algorithm”, Sustainable Computing: Informatics and Systems, vol.43, no.100991, 2024.
[26] Ferahtia, Seydali, Azeddine Houari, Hegazy Rezk, Ali Djerioui, Mohamed Machmoum, Saad Motahhir, and Mourad Ait-Ahmed, “Red-tailed hawk algorithm for numerical optimization and realworld problems,” Scientific Reports, Vol. 13, no. 1, 2023.
[27] Dovelos, K., Matthaiou, M., Ngo, H.Q. and Bellalta, B., “Channel estimation and hybrid combining for wideband terahertz massive MIMO systems”, IEEE Journal on Selected Areas in communications, vol.39, pp.1604-1620, 2021.
[28] Janod, K., Morchid, M., Dufour, R., Linares, G. and De Mori, R., “Denoised bottleneck features from deep autoencoders for telephone conversation analysis”, IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol.25, pp.1809-1820, 2017.