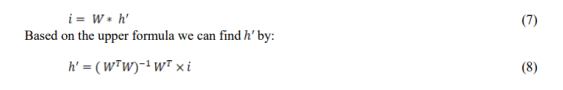IJCNC 03

HIGH PERFORMANCE NMF BASED INTRUSION DETECTION SYSTEM FOR BIG DATA IOT TRAFFIC

Abderezak Touzene, Ahmed Al Farsi, Nasser Al Zeidi
Department of Computer Science, College of Science, Sultan Qaboos University, Oman

ABSTRACT

With the emergence of smart devices and the Internet of Things (IoT), millions of users connected to the network produce massive network traffic datasets. These vast datasets of network traffic, Big Data are challenging to store, deal with and analyze using a single computer. In this paper we developed parallel implementation using a High Performance Computer (HPC) for the Non-Negative Matrix Factorization technique as an engine for an Intrusion Detection System (HPC-NMF-IDS). The large IoT traffic datasets of order of millions samples are distributed evenly on all the computing cores for both storage and speed up purpose. The distribution of computing tasks involved in the Matrix Factorization takes into account the reduction of the communication cost between the computing cores. The experiments we conducted on the proposed HPC-IDS-NMF give better results than the traditional ML-based intrusion detection systems. We could train the HPC model with datasets of one million samples in only 31 seconds instead of the 40 minutes using one processor), that is a speed up of 87 times. Moreover, we have got an excellent detection accuracy rate of 98% for KDD dataset.

KEYWORDS

Intrusion Detection Systems, Machine Learning, Dimensionality Reduction, High Performance Computing, IoT traffic.

1. INTRODUCTION

Based on reports published by cybersecurity institutions in several countries worldwide, network cyber-attacks have increased exponentially in recent decades. These days, as we witness the era of the Fourth Industrial Revolution (4IR) and its emerging technologies like the Internet of Things, Quantum Computing, and Artificial Intelligence. Millions of users have become connected to the Internet, and hundreds of millions of devices connected to the network produce millions of network traffic records datasets. Storing and analyzing those massive network traffic datasets using a single computer become difficult and highly inefficient especially when it comes to detection and prevention of traffic attacks on real-time.

Many machine learning algorithms can deal with relatively large datasets dimensionality reduction techniques for faster analytics, but it takes much time as the dataset size increases, Big Data. Therefore, it is necessary to use High Performance Computer and parallel implementation of machine learning algorithms to overcome both the storage and speed limitations.

This paper will focus on parallel Nonnegative Matrix Factorization using a High Performance Computer (HPC) using Message Passing Interface (MPI) for processors’ communication to implement an efficient real-time intrusion detection system to Big Data Analytics for large scale IoT traffic datasets. Nonnegative Matrix Factorization (NMF) is an approximation numerical method aiming at decomposing data matrix A into its simpler factors lower-rank matrices H and W. NMF is an unsupervised Machine Learning technique widely used in data mining, dimension reduction, clustering, factor analysis, text mining, computer vision, and bioinformatics, image recognition and recommendation systems to name a few. In contrast to Singular Value Decomposition (SVD) and Principal Component Analysis (PCA), Nonnegative Matrix Factorization (NMF) requires that A, W, and H be nonnegative. For many real-world data, nonnegativity is inherent, and the interpretation of factors has a natural interpretation which could be one of the advantages of NMF compared to PCA and SVD.

Formally, Nonnegative Matrix Factorization problem is to find two low-rank factors matrix and for a given nonnegative matrix , such that A ≈ WH. Most of the available optimization techniques include Hierarchical Alternative Least squares HALS, Multiplicative Updates (MU), Stochastic Gradient Descent, and Block Principal Pivoting (ALNS-BPP), which are based on alternating optimizing W and H while keeping one of them fixed.

1.1. Intrusion Detection System Background

This section discusses the background of Intrusion detection systems, including their definition and diverse types. Moreover, it discusses several papers on machine learning IDS algorithms.

1.1.1. Intrusion Detection System(IDS)

An intrusion Detection System is defined as a hardware device or software that observes systems for malicious network traffic or policy violations. The purpose of IDS is to detect various types of malicious network traffic or malicious computer use that a firewall cannot recognize. This is critical to achieving high protection against actions threatening computer systems’ availability, integrity, or confidentiality [1].

1.1.2. Types of Introduction Detection Systems(IDS)

There are many classifications for intrusion detection systems (See Figure 1). However, this classification has been used extensively in previous studies based on the data collection method:

1. Network intrusion detection system, which observes and analyses data traffic to detect if there is an attack or malicious behavior (NIDS).
2. The Host-based intrusion detection system monitors and analyses data from log files (HIDS), and based on the detection technique, it can be categorized into three main categories: Specification-based IDS, Anomaly-based IDS, and signature-based IDS.

Figure 1. Intrusion Detection Systems Classification

Signature-based (Misuse) Intrusion Detection Systems: Signature-based intrusion detection analyzes the network traffic, searching for occasions or combinations of similar to a predefined event pattern that describes a known attack.
Advantages: Signature-based Intrusion Detection Systems effectively detect intrusions without almost no false detections.
Disadvantages: Signature-based-IDS can only identify known attacks, requiring constant updating of the attack signatures. Signature-based-IDS detectors are trained very well for detecting specific types of attacks which may prevent them from detecting new kinds of attacks.

Anomaly-based Introduction Detection Systems: Anomaly-based intrusion detection systems identify abnormal behavior on a network. Commonly attacks differ from regular legitimate network traffic; the IDS can detect them by analyzing these changes and differences. Anomaly IDS are trained well on normal network traffic from historical data collected. So, they can see abnormal behaviors easily.
Advantages: Anomaly-based Intrusion Detection systems can detect abnormal behavior, so they can detect an attack without any knowledge about it, only from their behavior.
Disadvantages: Because of the variations in users and network behaviors, Anomaly-based IDS may fire many false alarms. Anomaly detection approaches must be trained in huge datasets of normal behavior activities.

1.2. Motivation

In this paper we aim at overcoming some of the limitations existing in traditional machine learning-based Intrusion Detection Systems (IDS), such as a considerable amount of training and testing on Big data datasets and to detect multiple types of attack in real-time. In this study we analyse the performance of ML-based IDS using KDD and CIC datasets by applying NMF, which will help reduce the datasets dimensions into lower-rank matrices that can be used for analysing and testing any new network traffic in real time.

The rest of the paper is structured of the remaining as follows: In section 2, will start with a brief background on Machine Learning based IDS and NMF and introduce the related work on which the proposed solution will be built. In section 3 will discuss the design of the proposed HPC parallel NMF based IDS including the learning and the detection phase. Section 4 is dedicated to the experimental work, it describes the implementation environment and the datasets used, and the performance evaluation of our IDS. Finally, section 5 will summarizes the paper and highlights some limitations along with the future works.

2.BACKGROUND AND RELATED WORK

This section will discuss the background of Machine Learning IDS and the background related to the Nonnegative Matrix Factorization (NMF).

2.1. Machine Learning-based IDS

Many recent Anomaly Intrusion Detection Systems (AIDS) is based on Machine Learning methods. There are a lot of ML algorithms and methods used for ML-based IDS, such as neural networks, nearest neighbor, decision trees, and clustering methods, applied to discover the meaningful features from IDS datasets [1] [2].

2.1.1. Supervised Learning in Intrusion Detection System

Supervised ML-based IDS techniques that can identify attacks based on labeled training datasets. A supervised ML technique can be divided into training and testing. Training phase, important features are specified and processed in datasets, then we train the model from these datasets. There are many applications of supervised machine learning-based IDS. Li et al. [3] used an SVM classifier with an RBF kernel to classify the KDD 1999 dataset into predefined classes. From a total of 41 attributes, a subset of features was carefully chosen by using the feature selection approach [3]. K-Nearest Neighbours (KNN) classifier: The k-Nearest Neighbour (kNN) method is a typical non-parametric classifier used in machine learning [4]. These methods aim to name an unlabelled data sample to the class of its k nearest neighbours.

2.1.2. Un Supervised ML-Based Intrusion Detection System

Unsupervised ML can be defined as an ML technique that obtains information of interest from input data sets without class labels. The input data points are usually treated as a set of random variables. A standard density model is then generated for the data set. In supervised learning, output labels are presented and used to train the machine to obtain the desired results for an unseen data point. By contrast, in unsupervised learning, no label is provided. Instead, the data is automatically grouped into different categories through the learning process [5].

2.2. Non Negative Matrix Factorization (NMF)

Non-negative matrix factorization is an algorithm that takes a nonnegative input matrix and decomposes it into lower rank matrices W and H based in low rank parameter K. NMF is an unsupervised Machine Learning technique commonly used in clustering, dimensionality reduction, factor analysis, data/text mining, computer vision, bioinformatics, image recognition and recommendation systems to name a few. In contrast to Principal Component Analysis (PCA) and Singular Value Decomposition (SVD), NMF requires that A, W, and H be nonnegative. For many real-world data, non-negativity is inherent, and the interpretation of factors has a natural interpretation which could be one of the advantages of NMF compared to PCA and SVD [10] [11].

2.2.1. Foundations of Non Negative Matrix Factorization Framework

NMF takes a nonnegative input matrix is number of rows which represent number of features and is number of column which represent number of samples, and low rank parameter which is positive integer < { }, NMF algorithms aims to find two low rank matrices and such that . NMF aims to minimize the following cost function:

Most of the available optimization techniques include Hierarchical Alternative Least squares HALS, Multiplicative Updates (MU), Stochastic Gradient Descent, and Block Principal Pivoting (ALNS-BPP), which are based on alternating optimizing W and H while keeping one of them fixed. NMF-IDS system consist of three major phases. In phase 1 the network dataset file is converted into a two dimensional matrix . In phase 2, the matrix will be factorizedinto two low-rank matrices and . Phase 3 consists of the detection phase. The same phases will be conducted for the parallel High Performance Computing distribution HPC-NMF- IDS.

2.2.2. NMF Factorization Phase
Lee and swing [6] proposed a multiplicative updates algorithm (MU) to solve the NMF factorization problem where the factor matrices W and H are updated using the following formulas:

HT means the matrix transpose of the matrix . MU algorithm can be divided into individual smaller sub problems of matrix dot product. Instep 1 we update W based on , and ,then in step 2 we update H based on , and . See algorithm 1 below.

Algorithm (1)

The while loop at algorithm 1 will stop if the stopping criteria are satisfied. Either it reaches the maximum number of iterations specified by the user, or it reaches convergence based on the Frobenius norm function .

2.2.3. NMF Detection Phase
After MU algorithm reach to convergence or it reach the maximum number of iterations specified by the user, we obtain the factor matrices W and H, that can be used to represent every sample from A as weighted linear combination of columns of W, every column of W called bases where the corresponding called the weights or encoding.

Now if we have a new sample let’s call it and we want to check if it matches one or more of the samples from the training set, we compute the encoding of it using :

Now we check the similarity of this encoding with every encoding that existed in H. The closest match (sample class) is that sample whose encoding is the closest to the new sample (multi-class detection). We can determine the matching score between the encodings using the following formula:

2.3. Related Work
2.3.1. Serial NMF-based IDS
X. Guan in [7] presented an efficient and fast anomalous intrusion detection model that includes many data from different sources. A new method based on non-negative matrix factorization (NMF) is discussed to characterize program and user behaviors in a computer system. A large amount of high-dimensional data was collected in their experiments. NMF was used and reduced the vectors to a smaller vector length after that, any simple classifier can be implemented in low dimension data instead of the entire dataset. After getting low dimension features the model can differentiate between normal traffic and abnormal traffic easily by using a threshold, so any user behavior on that threshold will be considered an attack.
Limitations: Although the implemented NMF-based IDS gives good accuracy, the datasets were nonstandard. Moreover, the threshold technique used in the testing phase could not be applied to multi-class network attacks.

2.3.2. Parallel NMF
In order to overcome the limitation of low performance NMF when applied to a larger dataset. scientists have proposed parallel NMF and applied it in different ways, we will discuss here two approaches, the first is based on MapReduce, and the second is based on Message Passing Interface (MPI).
2.3.2.1. Hadoop Map Reduce based Parallel NMF
Yin et al., 2018 [12] proposed scalable distributed Nonnegative Matrix Factorization based on Hadoop Map Reduce for different application. See Figure 2.

Figure 2. Map Reduce Applications

The authors proposed a technique for NMF matrix update by using block-wise updates in an efficient MapReduce implementation. Moreover, they propose frequent and lazy block-wise updates to optimize the operations. They claimed that their solution is faster than any existing MapReduce NMF implementation with a traditional NMF update algorithm.
Limitations:
Although their implementation can handle larger files efficiently, the reported results for NMF algorithm time are relatively large. See Figure 2. It is meanly due to Hadoop Map Reduce-based algorithms with involving read/write data to/from disk which affecting the algorithms’ performance.
2.3.2.2. Message Passing Interface based NMF
MPI-FAUN by R. Kannan et al. 2018 [13] overcomes the Hadoop implementation as it shows better speedup results. They test their algorithm in more extensive datasets of order millions x millions in seconds using MPI-based parallel high-performance NMF. See Figure 3.

Figure 3. MPI based applications

The authors proposed a parallel distributed high-performance NMF framework based on MPI that iteratively updates the low-rank factors in an alternating fashion. The framework proposed can be applied with many different NMF update algorithms, giving efficient results for dense and sparse matrices of massive sizes of hundreds of millions of datasets. The framework parallelism is designed to use minimum communication and it can scale up to more than 1000 cores.

Figure 4. Processors data distribution

Data Distribution:
They divided the matrix W into blocks of rows equal to the number of processors p, ( )

and the matrix H into blocks of columns ( ). Then, based on this distribution, matrix the A is distributed by rows ( ) and also by columns ( ), as shown in the Figure 4, so that processor has column and row . Using this distribution Alternating Update algorithm such as Multiplicative Update (MU) or Hierarchical Alternative Least Square (HALS) implemented
Limitations: As far as it is linked to our research, the authors were only interested to develop a
parallel version of NMF without testing on specific application. In this paper, we use the same methodology, apply it and test it in the context of developing a real-time Intrusion Detection System using our University High Performance Computing facility.

3.PARALLEL NMF-IDS PROPOSED SOLUTION

This section will discuss the proposed solution of distributed parallel NMF based IDS in the HPC of Sultan Qaboos University (Luban).

3.1. Proposed Solution
This section discusses the proposed solution for the problem of low performance (Speed and accuracy) of Machine Learning Anomaly Intrusion Detection System when dealing with huge datasets of orders of millions of samples.

3.1.1. NMF based Intrusion Detection System
KDD99 and CIC datasets (discussed in section 4.3) are Big data sets contains millions of network traffic data. Based on the results of the above-mentioned literature, NMF based IDS has proven to give better performance than other ML based AIDS, in terms of speed of training/testing high dimensional datasets and accuracy. Therefore, NMF was selected. The initial experiment on NMF based IDS (one processor) showed promising results.

3.1.2. Parallel NMF based Intrusion Detection System
Although NMF-based IDS showed good performance in relatively small datasets, it showed, based on the experiments, to take a lot of time for larger datasets. In this study, we solved this issue by applying parallel MPI-based NMF implemented on high-performance computing Luban (section 4.2).

As mentioned in section (2.1.1), the non-negative matrix factorization algorithm aims to decompose input matrix into the low-rank matrices and . Lee and swing [6] proposed a multiplicative updates algorithm (MU) to solve the NMF problem. The matrices W and H are updated using the following formulas:

Where means the matrix transpose of the matrix . MU algorithm can be divided into individual smaller sub-problems of matrix dot product. In step 1 we update W based on ,HHT and , then in step 2 we update H based on , and . Looking at the

dimensions of the matrices involved on each dot product operation, we can see that and have low dimension only . So, they can be solved in all processors without distribution to reduce communication costs. Now, to solve the rest of the operations in parallel, we divided W into blocks of rows equal to the number of processors (W1,…..,Wp) and the matrix H into blocks of columns (H1,…Hp). Then, based on this distribution, we distributed the matrix A, once by rows (A1,…,Ap) and once by columns (A1,…,Ap), as shown in Figure 5, so that processor I has column A i and row Ai.

Figure 5. Parallel data distribution and communication

With this distribution of data and variables, we can now apply parallel MU algorithm using only two communications per iteration. As shown in algorithm 1. we can solve in several parallel instances of equations 4 and 6 to update and , respectively. In equation 3, we apply MPI allgather to gather parts of the updated matrix from each processor and distribute the full matrix to all processors. We do the same process for in equation 5.

Algorithm (2)[W,H]=Parallel_NMF(A,k)

The all-gather communication steps allow to collect from all processors the updated row blocks of Wi and the columns blocks of H I to form the matrices W and H on each processor in order to start a new iteration.

4.IMPLEMENTATION OF HPC-NMF-IDS AND EXPERIMENTAL RESULTS

We will explain the implementation environment starting by explaining the software and hardware specification of Luban High performance Computing system at Sultan Qaboos

University. Then the data sets used in this study will be described. After that, the parallel multiplicative update algorithm will be discussed, the rest of the section will show the performance of the results.

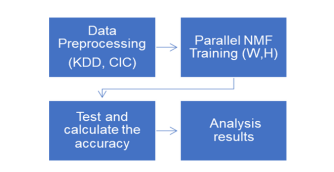
4.1. NMF-IDS Methodology
In this study we will test our NMF-IDS on two known datasets (KDD, and CIC) after a preprocessing phase, training phase using NMF factorization eq. 4, 5, and detection testing eq.7, 8, 9.

Figure 6. HPC-NMF-IDS Methodology

4.2. High Performance Computing (Luban) @ SQU
Luban is a High Performance Computing system of Sultan Qaboos University (SQU), launched in February 2020. It provides 50 teraflops of computing power delivered using 15 advanced compute nodes with around 400 terabytes of storage space, all connected to a high-speed connection. The hardware and software specifications of Luban System are as follows. See
Figure 7:

● Compute Node Specification:
Each compute node (Think-System SD530): has Cent OS 7 Linux operating system, Dual 20- cores Intel Xeon Gold 6230 2.10GHz CPUs, 197GB RAM, 10Gb Ethernet interface, and 100Gb Intel Omni-Path Architecture (OPA) 100 Series.
● Login and Master Node Specification:
Each node (Lenovo Think-System SR630): has Cent OS 7 Linux operating system, Dual 14-cores CPUs, 197 GB RAM, and 480TB + 12GB (SSD) storage.

Figure 7. High Performance Computing Facility HPC Luban @SQU

4.3. Datasets

This section will discuss the datasets used in this study in detail and how we pre-process them. To study the performance of the proposed solution in this study, we applied it and analysed its efficiency and accuracy on two different datasets, namely KDD and CIC.

KDD99: KDD dataset is a dataset used in an international competition held at the University of California [8], where the goal of that competition was to build an intrusion detection system that can differentiate between a normal good connection, or a bad connection called an intrusion or attack. KDD dataset is about 5 million connection records that was generated from 7 days’ network traffic. It contains 41 features, and it is labelled by either Normal or specific type of attack. KDD contains attacks that can be categorized to Denial of service (DoS), Remote to local (R2L), and User to root (U2R).

CIC-IDS2017:The second dataset used in this study is CICIDS2017,created by I.Sharafaldin [9] from the Canadian Institute for Cybersecurity. It’s a benchmark dataset consisting of 2830743 samples and 78 features. CIC dataset contains more recent attacks. For example, Brute Force FTP, DoS, infiltration, DDoS.

4.4. Datasets Pre-Processing

This section explains the pre-processing methods for KDD and CIC datasets before applying NMF to them to get the best results.

Label Encoding: To apply NMF to any dataset, we must ensure that all elements within the dataset are non-negative numbers. The KDD dataset contains some features with text values namely, service, Protocol_type, and flag, so they need to be converted to numeric values using label_encoder from sk learn library of Python.

Normalization: Some features from the datasets contain large numbers. For example, src_bytes and dst_bytes from KDD have large values that can reach thousands. Also, in CIC dataset Flow_Duration contains values reach more than one million and Destination_Port can reach thousands, those great values may affect the model’s performance as it will be biased to those great values. Therefore, normalization is applied to ensure that all the dataset’s values are in the same range. In this study, we apply min-max normalization to make sure that all the values are ranged between 0 and 1 only.

Train/Test Split: We divided KDD and CIC datasets into several training data sizes to apply the proposed parallel NMF on it.
 Training datasets sizes (30K)
 Testing dataset size 3K
The original shape of the datasets was to reduce the number of features and to get correct results out from NMF we will transpose the input matrix so it will be on the following shape .

4.5. Experiments and Results
4.5.1. Experiment (1) Find Best Rank K for KDD Dataset
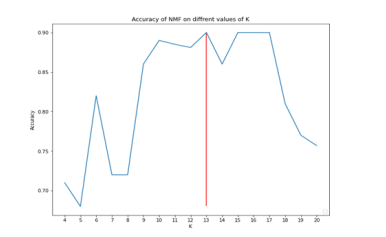
To make the most of NMF Algorithm, we must select the rank hyper-parameter carefully to ensure that it gives the best results by striking a balance of reducing the dimension of the problem and keeping the most amount of the features to insure good detection accuracy. In theory it is difficult to assess which rank K will be the best. We decided to select the best rank experimentally by running 1000 iteration of NMF with different values of K, as shown in Figure 8By analyzing the results of the experiments, was selected as it gives an accuracy rate reaching up to 98% in 1000 iterations.

Figure 8.NMF-IDS Best Rank selection for KDD

4.5.2. Experiment (2) Training & Testing on 30K samples KDD
Using as per the previous experiment, we implemented NMF on 30000 samples of42 features extracted from the KDD dataset.

Table 1.30K samples KDD dataset Results

As shown in the Table 1, increasing the iterations gives better results in terms the detection accuracy, at the expense of higher training time (factorization). As it is clear, NMF for one processor finished 100 iterations in approximately 4 seconds, with a detection accuracy of 76%, compared to 800 iterations in approximately 31 seconds, but with a detection accuracy of 98%.

Table 2.30K samples KDD dataset Results

Table 2 summarizes the results of running our proposed parallel NMF. We can reduce the training time from 39.5 seconds using 1 processor to 3.9 seconds using 4 processors which corresponds to a speedup of 10. This speedup is called super-linear speedup as it is more than number of processors (4). Super-linear speedup happened here because running NMF in one processor with a dataset that may not fit into its main memory, virtual memory using paging stored in the disk memory will be time consuming. On other hands, we noticed unexpected behaviour as we increase the number of processors the speedup decreases. This happens due to the cost of the communication between processors, which overwhelms the speedup in processing when the dataset is small.

4.5.3. Experiment (3) Training & Testing on 1M samples KDD
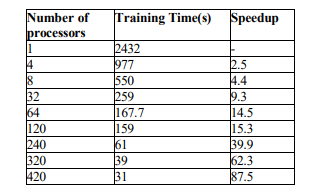
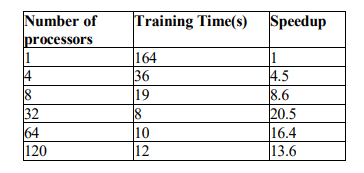
In this experiment we applied parallel NMF on one million samples of KDD, after one thousand iterations we got detection accuracy of 97%. The results using different numbers of processors are shown in Table 3.

Table 3.1M samples KDD dataset Results

In this experiment, as we can notice from Table 3, training the model using one processor took 2432 seconds, approximately 40 minutes. However, we reduced this large number using the Parallel NMF on 420 cores to be only 31 seconds, with a speedup of 87.5 times.
4.5.4. Experiment (4) Find Best Rank K for CIC Dataset
As the best selection of the rank K depends on the dataset, in this experiment we run different runs of NMF with different values of K for the CIC dataset, as it is shown in Figure 9. After1000. By analyzing the results of the experiments, was selected as it gives an accuracy rate reaching up to 90% in 1000 iterations.

Figure 9. NMF-IDS Best Rank selection for CIC

4.5.5. Experiment (5) Training on 30K samples CIC

Using based in experiment 4, we implemented parallel NMF on 30000 samples of CIC. Using different number of processors, we got the following results shown in Table 2.

Table 4. 30K samples CIC Dataset Results

As shown in the Table 4, increasing the iterations gives better results the accuracy rate is increasing but with an additional cost for training. NMF-IDS reaches a detection accuracy of 90% in 164 seconds.

4.5.6. Experiment (6) Training on 30K samples CIC parallel

Using the best rank from experiment 5, we implemented parallel NMF on 30000 samples of CIC. From Table 5, we notice a similar behavior compared to the KDD dataset in terms of speed-up due to the size of the dataset which is relatively small.

Table 5. 30K samples CIC dataset Results

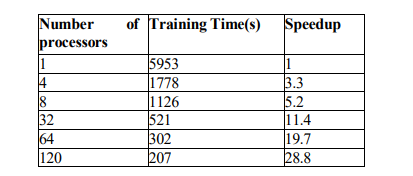
4.5.7. Experiment (7) Training on 1M samples CIC parallel

Using select in experiment 4, we implemented parallel NMF on one million samples of CIC. Table 6 shows a better speed up compared to smaller dataset 30K. Using 120 processors our parallel HPC-NMF-IDS manages to reduce the training time from 1.6 hours to 3.45 minutes.

Table 6. One Million samples CIC dataset Results

5.CONCLUSION

Millions of users and smart devices connected to the network produce several millions of network traffic records. Storing and analyzing those traffic datasets is a challenging task. In this paper we proposed a parallel and distributed Intrusion detection system based on dimensionality reduction using High Performance Computer facility for Non-Negative Matrix Factorization to be able to analyze efficiently large IoT traffic datasets. To achieve higher speedups using as many cores in the HPC, the NMF algorithm distributes the blocks of rows and columns of the matrices A, W, and H, by taking into account the data locality and minimization of the communication between the computing node. Unlike the previous work which focus only on binary classification of the network traffic, our implementation can detect multi-class of network attacks. Experimental results show a detection precision of 98% for KDD datasets and 90% precision for CIC dataset. In terms of efficiency for the HPC implementation, we could train our model using KDD dataset of order of a million of samples in only 31 seconds instead of the sequential implementation (one processor) which took approximately 40 minutes, that is a speed up of 87 times.

In our future work this study will investigate different approaches for data distribution distribute to make the most of the parallelism and reduce the communication overhead to the minimum possible. We will also investigate different update methods for NMF updates, including Block Principal Pivoting (BPP) and Hierarchical Alternating Least Squares (HALS) which may give faster results by reducing the number of iterations and thus the computation cost.

REFERENCES

[1] L. Xiao, X. Wan, X. Lu, Y. Zhang, and D. Wu, “IoT Security Techniques Based on Machine Learning: How Do IoT Devices Use AI to Enhance Security”,IEEE Signal Process. Mag., vol. 35, no.5,pp. 41–49, 2018

[2] N. Kshetri and J. Voas, “Hacking Power,” no. December, pp. 91–95, 2017.

[3] Y. Li, J. Xia, S. Zhang, J. Yan, X. Ai, and K. Dai, “An efficient intrusion detection system based on support vector machines and gradually feature removal method,” ExpertSyst. Appl., vol.39, no. 1, pp. 424–430, 2012.

[4] W. C. Lin, S. W. Ke, and C. F. Tsai, “CANN: An intrusion detection system based on combining cluster centers and nearest neighbors,”Knowledge-BasedSyst.,vol.78,no.1,pp.13–21,2015.

[5] A. Khraisat, I. Gondal, P. Vamplew, and J. Kamruzzaman, “Survey of intrusion detection systems: techniques, datasets and challenges,” Cybersecurity, vol. 2, no. 1, 2019.

[6] D. Leeand H.S. Seung, “Algorithms for Non-Negative Matrix Factorization,” in Advances in Neural Information Processing Systems, no. 1, 2000, pp. 556–562

[7] X.Guan, W.Wang, and X.Zhang, “Fast intrusion detection based on a non-negative matrix factorization model,” J. Netw. Comput. Appl., vol. 32, no. 1, pp. 31–44, 2009.

[8] S. Stolfo, “KDD-99 Dataset, ” online,1999. http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html (accessed Dec. 24, 2022).

[9] I. Sharafaldin, A. H. Lashkari, and A. A. Ghorbani, “Toward generating a new intrusion detection dataset and intrusion traffic characterization, ”ICISSP2018 -Proc.4thInt.Conf.Inf.Syst.Secur. Priv., vol. 2018-Janua, no. Cic, pp. 108–116, 2018.

[10] R. Hedjam, A. Abdesselam, and F.Melgani, “NMF with feature relationship preservation penalty term for clustering problems,” Pattern Recogn., vol. 112, 2021.

[11] T. Masuda, T. Migita and N. Takahashi, “An Algorithm for Randomized Nonnegative Matrix Factorization and Its Global Convergence, “2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 2021, pp. 1-7.

[12] J. Yin, L. Gao, and Z. Zhang, “Scalable Distributed Nonnegative Matrix Factorization with BlockWise Updates,” IEEE Trans. Knowl. Data Eng., vol. 30, no. 6, pp. 1136–1149, 2018, doi: 10.1109/TKDE.2017.2785326.

[13] R. Kannan, G. Ballard, and H. Park, “MPI-FAUN: An MPI –Based Framework for AlternatingUpdating Nonnegative Matrix Factorization,” vol. 30, no. 3, pp. 544–558, 2018.