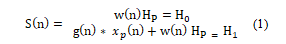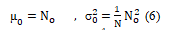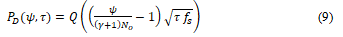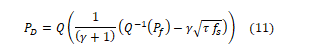IJCNC 05

Sensing Time Improvement Using Two Stage Detectors For Cognitive Radio System

Mohamed Khalaf 1*, Ahmed Fawzi 2† and Ahmed Yahya3†

1*Department of Electronics and Communications Engineering, Modern Academy for Engineering and Technology, Maadi, Egypt
2Department of Electronics and Communications Engineering, Modern Academy for Engineering and Technology, Maadi, Egypt
3Electrical Engineering Department, Faculty of Engineering (Cairo), Al-Azhar University, Cairo, Egypt

ABSTRACT

Cognitive radio (CR) is a promising technology for both present and future telecommunications to satisfy the demand of the next generation due to inefficient use of the allocated spectrum. Due to its ability to utilize the available bandwidth of other wireless communication networks and so enhance its occupancy. Spectrum sensing (SS) is the key characteristic of the CR system that helps it identify the empty spectrum. SS has gained a lot of interest recently and it is an active research area since it offers additional opportunities to secondary users. A broad variety of analytical methods to identify the Primary User’s (PUs) presence have emerged as a result of SS techniques for CRs. Although each approach has its own benefits, the drawbacks attached to them make an individual implementation of the technique impractical for usage. To mitigate the drawbacks and maximize the benefits offered by the individual methods, a two stage detector can be employed for SS. However, the stages method lengthens the time needed to sense the spectrum and produce a definitive result. In this paper, we propose a two-stage sensing approach, where the first stage is an Interval Dependent Denoising detector (IDD) and followed by a second stage is Energy Detection (ED) which provides a large decrease in the mean sensing time compared to different related two-stage SS approaches The ED method is simple and has a short sensing time, but it performs poorly when the Signal to Noise Ratio (SNR) is low, Hence it is thought that separating PU activity from noise is essential for accurate SS. Therefore, we use IDD as a noise reduction technique in the first stage before the ED stage. The simulation results have been utilized to demonstrate that this technique leads to a large savings in sensing time as compared to an existing two-stage detection approaches.

Keywords:
Cognitive radio (CR), Spectrum sensing (SS), two stage detection, energy detection (ED), mean detection time, interval dependent denoising detector (IDD).

1. INTRODUCTION

As wireless communication grows rapidly, it becomes increasingly crowded due to inefficient bandwidth use across different spectrum bands, which is a one of the major drawbacks of traditional wireless networks with limited bandwidth deployment constraints. In accordance with estimation of expected communications-related needs, in the next years, it’s predicted that the spectrum will expand even further. However, the current spectrum shortfall is largely as a result of ineffective fixed spectrum allocations than physical shortage of spectrum. The conventional fixed spectrum assignment policy is a big hurdle in the innovation of new technologies is supported by recent studies of the Federal Communication Commission (FCC) allowed the unlicensed fixed and personal/portable devices in rural and urban area [1, 2].

CR has been recently seemed as an effective method to increase spectrum utilization through opportunistic spectrum sharing in order to resolve the conflicts between spectrum under-utilization and congestion. CRs are intelligent communication technology that can recognize their wireless surroundings and decide when and how to use the available spectrum (white space), which is not being used by the authorized user. To avoid causing damaging interference to main users, CRs must be capable of scanning wide frequency ranges and detecting unoccupied bands [3]. The CR must sense the spectrum’s availability before accessing the channel in order to implement without interfering with the primary signal [4].

The primary purpose of CR is SS to identify PU / licensed user; if PU is not present, spectrum is then available to Secondary User/cognitive radio user (SU), and this area is known as a “spectrum hole” or “white space”. SS is a process for detecting PU by sensing the surrounding radio environment [5-7]. The fundamental concerns of SS revolve on two issues: first, SU communication should not interfere with the primary system, and second, spectrum holes should be efficiently identified for the desired throughput and Quality of Service (QoS) [8].

There are several techniques for SS that are determined, such as matching filter, ED [3] and Cyclostationary Feature Detection (CFD) [9, 10]. The received SNR in communication systems is maximized by the matched filter, so it is the optimal technique. However, a key disadvantage of a matched filter is that it required previous knowledge of the signal of the PU, including the type and order of the modulation, the pulse shaping, and the packet format. CD offers reliable SS, even at low SNRs and it is based on the autocorrelation function, but it is computationally complicated and necessitates longer sensing time. On the other hand, one-order CD [11, 12] is conducted in the time domain. The mean characteristic of the PU signal is used in one-order CD to increase the effectiveness of the channel sensing. Therefore, less computational complexity and real time operation can be accomplished by the one-order CD. on the other hand, ED is a simple approach with a short sensing time, but it performs poorly in low SNR conditions. There are also other additional approaches to detect the spectrum such as maximum-minimum eigenvalue detectors, which may simultaneously achieve high detecting probability and low false-alarm probability without requiring PU prior information [3].

The detection rate and  serve as indicators of the sensitivity and selectivity, which together forms the metrics for spectrum sensing performance. The probability that SU announces that PU is present when the spectrum is vacant is known as the ; in contrast, the probability that SU announces that PU is present when the spectrum is occupied by PU is known as the . The probability that SU will announce that PU is not present when the spectrum is in use is indicated by the probability of missed detection. Due to the fact that false alarms decrease spectrum efficiency and miss detection causes interferes with PU, achieving the highest while maintaining the lowest  is essential for the best detection performance [13].

According to the IEEE 802.22 standard [14], PUs must be identified within two seconds, and  and missed detection must be less than or equal to 0.1 [15]. To guarantee that the spectrum resources are completely utilized without interfering with PUs’ communication, the sensing time must not exceed 2 seconds [16]. It is not possible to transmit data while also sensing the licensed spectrum. Therefore, for effective use of spectrum holes, SU must periodically sense the band at sensing period every Tp seconds. Due to SU’s not being aware of its activities through the sensing interval, or until the next sensing moment, PU transmission may be prevented. As a result, the sensing period has a major impact on PU performance. Maximizing the sensing period may enhance SU throughput, but may make PU prevented because PU is rarely sensed. From the viewpoint of a CR network, SU wants to increase the sensing period and reduce the sensing time to increase transmission time [17]. To cohabit with the licensed band, the SU must correctly schedule the sensing period. The SU can increase throughput and minimize PU interference while maintaining sensing reliability by minimizing the sensing time. In CR networks, maximizing PU detection reliability and reducing sensing time are two key considerations for efficient SS. In this paper, a two-stage sensing model for spectrum detection is developed to increase sensing efficiency by increasing  while staying within the parameters of the and obtaining a low mean sensing time. The rest of the paper is arranged as follows. Section 2 displays a brief discussion of various related work on two-stage SS methods.  The system model of the sensing approach is shown in Section 3; Section 4 includes simulation results for evaluating the proposed model performance in terms of detection performance and mean detection time and finally conclusions are noted in section 5.

2. RELATED WORK

According to the benefits and drawbacks of the methods mentioned above, it can be concluded that no single technique is perfect enough to be used on a CR device. As a result, it would be preferable to combine two or more techniques in order to mitigate the drawbacks of the techniques while utilizing the individual benefits of the techniques. This kind of synergy may be used to establish algorithms that have quick sensing time even in low SNR situations and can achieve the required probabilities of detection and false alarms. Thus, recent paper on SS is concentrating on two-stage spectrum detection. The authors of Ref. [18] suggest a two stage sensing approach for dynamic spectrum access, which has been studied. The authors divided the sensing techniques into two stages: coarse and fine sensing. The first stage is coarse sensing based on ED, and if needed the second stage is fine sensing based on CD. Only if a channel is identified to be vacant in the coarse stage the fine stage is employed and will take the final decision .If not, coarse sensing will take the final decision. Another two-stage sensing mechanism was presented by the authors in Ref. [19]. Multiple Energy Detectors (MED) are performed in the first stage, where each energy detector (ED) consisting of a single antenna and with a fixed threshold (MED FT) for making a local binary decision, and if needed, the second stage, which is constructed of ED with Adaptive Double Threshold (ED ADT), is activated with this technique, computing complexity is reduced, but sensing time is increased. The authors of Ref. [20] use a two adaptive local SS technique in which CR can utilize either an ED or a one-order cyclostationary for SS based on expected SNR, which is determined in advance for available channels. The proposed technique uses the ED to provide rapid detection at high SNRs. at low SNRs since ED is unreliable, the proposed technique offers improved detection at the cost of longer mean detection time.

Two-stage SS approaches are suggested by the authors in Ref. [21]. They used two-stage detectors in the general case, An ED is the first stage followed by a Covariance Absolute Value (CAV) in the second stage. The authors used the two stages for all the received signals with variable SNRs. In a modified method, only when the SNR is higher than a specific threshold the second stage of the CAV detector is activated. Based on Estimated SNR with Adaptive Threshold (ESNR ADT), the authors of [22] provided a unique collaborative SS method in CRN. The proposed scheme evaluates SNR and chooses an ED with either a fixed threshold or an adaptive threshold to improve detection performance at a fixed  = 0.1. Based on the estimated SNR value and the first threshold, the detector is selected. If the estimated SNR value exceeds or is equal to this threshold, an ED with the second threshold will be employed; else, an ED with ADT will perform sensing processes. Although this technique decreases mean sensing time less than CD, it does not take into account the issue of SS failure. In [23], the authors suggested a two-stage sensing approach for CRs, where the first stage involved ED and the second, CD. The detection parameters are used in both stages to enhance the within the boundaries of the , although it is computationally more complex and needs a longer sensing time. The authors of Ref. [24] presented an improved two-stage detection (improved-TSD) method for SS. The improved-TSD technique consists of two stages: the first stage contains two detectors, namely an ED using a single adaptive threshold (ED SAT) and an ED using two adaptive thresholds (ED TAT), which are arranged in parallel, and the second stage includes a decision device (DD) that creates the final decision using the OR-rule. The proposed sensing technique reduces the sensing time.

With the aid of the two stages ED and CD discussed in [18], however the elapsed time by a two stage detector is still high because of the complexity of the second stage. Better performance features are presented by the authors In Ref. [25]. As a result, the second stage detector can be used intelligently and decreasing the time taken to reach a conclusive decision. The decrease in the mean detection time of the SS algorithm in this method illustrates the advantage of reduction in the activation of the second stage. It was further shown that the suggested modification has no bad effect on of the CR and the authors did not consider uncertainty in their estimation of the noise power for the ED stage. In Ref. [26], a hybrid sensing model for spectrum detection in CR is executed. The first path is constructed from two sequential sensing stages; in the first stage, an ED is used to identify the presence of the PU signal when the signal has not been detected. The presence of the PU signal is detected using a second stage called Maximum-Minimum Eigen value (MME). The second path composed of two parallel stage detectors employing separate ED and MME to detect the PU signal separately. The two results are brought together to form a decision, and the final decision is taken using the combined results of the two paths’ detection. The suggested hybrid sensing method, used to improve sensing performance, is validated using traditional techniques but it suffers from computational complexity.

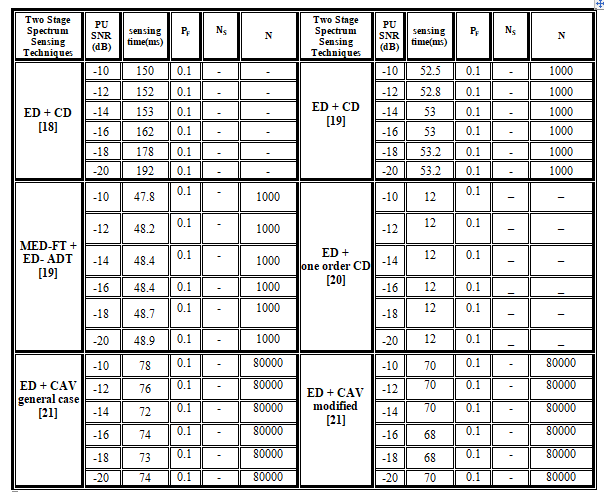
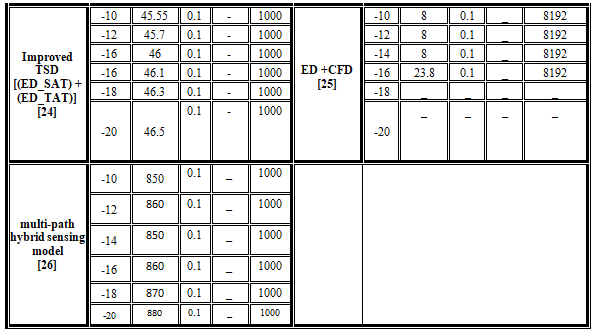
Tables [1, 2] show a summary of the previous related works of two stage SS methods [18-26]. This table provides a thorough comparison of the related two stages prior research in terms of SNR for PU signals (SNRp), sensing time)ms), , and number of sensing samples N. the tables provide a complete comparison of the earlier efforts. According to prior research, it has been shown that the various two-stage SS approaches have a tendency to have a high computing complexity, high sensing overheads, low and medium sensing accuracy, and bad performance in uncertain noise environments. Finally, we observe that in the situation of low SNR values, the step of distinguishing between PU signals and noise is missing. The ED technique alone cannot be utilized to make decisions about the main user (PU) condition when the SNR is low. So, the IDD detector step is utilized before to the ED to minimize noise and identify the PU signal in the presence of noise. As a result, we offer an alternative implementation of the two stage detection techniques which can help in substantial savings in the sensing time required to compute an accurate result while maintaining the target detection and false alarm probabilities of the CR device.

Table 1. Comparison of the related works on two-stage SS methods

Table 2. Comparison of the related works on two-stage spectrum sensing methods

3. THE PROPOSED MODEL

Noise impacts the received signal randomly and can be produced by a variety of factors, including time-varying thermal noise at the communication system’s receiver and noise interference from the surrounding environment. Furthermore, a variety of factors, such as electromagnetic interference, affect the received signal. So noise reduction is one of the most challenging issues in communication systems, and it has gained much attention recently. Noise cancellation methods and technologies have evolved in response to the requirement for reducing unwanted noise in desired signals. Wavelet transform (WT) has been shown in high-performance signal processing tool [27-29] to be a particularly efficient technique for de-noising signals when compared to conventional approaches such as the Fourier filter and Savitzky-Golay filter [30].

 Wavelet de-noising With WT, the signal’s time and frequency characteristics are presented, and the resulting approximation and detail coefficients reflect the low and high frequency components of the signal under analysis, respectively. As noise is mainly composed of high frequency components, noise reduction is accomplished by thresholding the detail coefficients. The de-noising process typically consists of the following three steps:

• Decomposition: the noisy signal is converted into a collection of orthonormal wavelet basis functions, selecting a mother wavelet and a maximum decomposition level followed by computing the decomposition coefficients at each level.
• Thresholding: In this stage, the threshold values for each level are evaluated, and the coefficients at each level are applied to the threshold.
• Reconstruct: Using the inverse wavelet transform, the signal is rebuilt using the modified coefficients.

Hence the packet of wavelet technique is a generalization of wavelet decomposition that provides a wide variety of signal analysis scales. In packet wavelets analysis, the details as well as the approximations are divided into  different ways to represent the signal where the decomposition level is n. Several bases are produced by single wavelet packet decomposition, which provides a more complicated and adaptable analysis. The best level of signal decomposition is chosen using an entropy-based criterion. Fig. 1 displays the packet of wavelet decomposition and reconstruction trees.

The input signal  is divided by using filters   and  into a low pass component  and a high pass component , which are decimated (down-sampled) by factor two. The low pass component is then divided more into  and , which are again decimated by factor two. This procedure is repeated as needed. The DWT outputs are the band pass coefficients , , ,……, and the last low pass coefficients  The decimation ensures that the input sample rate and total output sample rate are identical, so there is no redundancy in the transform. The signal is reconstructed using a pair of reconstruction filters  and  are utilized in the configuration of Fig. 1 where  may be reconstruction from   and ; and then  from  and ; and so on back to , using an inverse tree of  filters.

Figure 1. packet of wavelet decomposition and reconstruction trees

When a noisy signal is de-noised using the WT approach, the accuracy of the reconstructed signal is determined by both the thresholding method and the threshold values. There are two fundamental methods for compressing wavelet coefficients: hard thresholding and soft thresholding [31, 32]. Several methods for selecting thresholds have been studied [33]. Standard techniques contain level-dependent and interval-dependent threshold selections. The level thresholding method, which selects a single universal threshold for each level then applies it to threshold all coefficients at the selected level. To threshold the coefficients within each interval, the interval thresholding approach first divides the coefficients at each level into blocks and then chooses a local threshold for each interval. This signal division makes the heteroscedastic noise be approximately homoscedastic noise within each interval, enhancing de-noising efficiency, So the proposed two stage model using IDD and ED for detecting the PU signals, especially in the case of low received PU Signal to Noise Ratio (SNRp), is used to improve the sensing performance as demonstrated in the simulation result below because it obtains a higher  and a lower , even at low SNRs and gains minimum sensing time due to the simplicity and less complexity of the proposed method. Flowchart of the proposed model is shown in Fig. 2. The IDD stage is used for noise reduction and for extraction of the PU signals from noise at low PU SNR to perform reliable detection and accurate SS.

Figure 2. Flowchart of the proposed model

The ED detector is performed in the second stage due to its efficiency and simplicity. To compute the energy of the received signal, the samples are squared and integrated during the observation period; the integrator output is then compared to the threshold. If the integrator’s output higher than the threshold, it will be assumed that the given radio spectrum is occupied. Otherwise, it is considered to be empty. The following hypothesis for received signal [34] can be applied to identify the PU signal

where the received signal is represented by  and the channel gain is represented by , the PUsignal of a transmitted power , the additive white Gaussian Noise (AWGN) at the cognitive user receiver is represented by , which is considered to be a Circularly Symmetric Complex Gaussian (CSCG) random process with zero mean and one-sided power spectral density  (i.e., ), and represents the time index. The null hypothesis is represented by , which represents the absence of PU and the alternative hypothesis is represented by , which represents that PU is present.

For ED, the decision factor is computed by the energy of the samples that were taken during the observation window duration τ, and it is expressed by:

Where N represents the number of sensing samples (  with  indicating the sampling frequency

By comparing the decision factor with a predefined threshold  the probabilities of false alarm and detection can be determined, which determines under the both hypothesis  and , respectively.

And can be determined as follows:

    Where denotes the complementary distribution function of the standard Gaussian

The decision factor has a normal distribution then the mean and variance have been shown as:

Let represent the SNR of the received signal

After substitution of mean and variance values:

To ensure that a PU network is effectively protected from harmful interference from a secondary network, typically a limitation is adopted on the targeted , especially in a low SNR environment. In IEEE 802.22 WRAN, the targeted probability of detection  for the SNR of  dB

For the target the decision threshold can be obtained from Equation (9) as follows:

It can rewrite them such that one is a function of the other. The detection probability is related to the false alarm probability as follows:

The IDD technique is implemented in the first stage for noise reduction and efficient SS process, in signal de-noising applications Wavelet transformation is widely employed the sampled signal inside the band of the licensed user must always be processed by the CR. the system equations in (1) are simplified as follows:

The wavelet transform of the received signal is shown as follows:

 

Where W is the left invertible transformation matrix of the DWT, because  contains few changes the detail information of is sort of zero. Therefore, the detail information contains the details that indicate the majority of the noise power in the wavelet transformation domain. After thresholding the detail information, the inverse wavelet transform can recover the desired signal with less noise effect which increase the ability to distinguish between the signal and noise which improving the accuracy of ED technique. Finally, the proposed method assists in overcome the problems of high  rates, poor detection accuracy at low SNR levels, and noise uncertainties and helps to gain minimum sensing time which required in CR networks.

4. SIMULATION RESULTS FOR THE PROPOSED MODEL

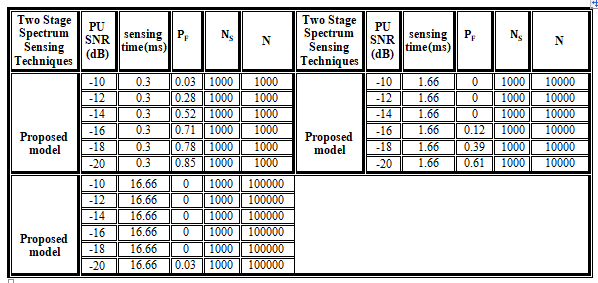
In the presented system model, the simulation results and analysis of the proposed model are executed in MATLAB, using the sampling frequency of 6 MHz, a zero-mean additive white Gaussian Noise and one-sided power spectral density  = 1 over 1000 Monte Carlo simulations, at low SNRs most previous techniques are not robust to noise, therefore impacting CR’s performance and reliability. The simulation is performed at an SNR varying from −10 to -20 dB which is the most common range for low SNR in previous related two stage methods and N varying from 1000 to 100000, P ( = 0.2 and the targeted  = 0.9 according to IEEE 802.22 WRAN. The time needed by CR user to detect the licensed PU signal is the SS time. The PU can make more efficient use of its band if the sensing time is increased and the limit is set so that CR user is unable to interfere with PU at that long time. The longer spectrum sensing, the more PUs will be detected and the less interference will occur since PUs can make maximal utilization of their priority right. The sensing time is directly proportional to the samples number received by the CR user. Table 3 contains the result of  of the proposed model at different signal to noise ratio at N equal 1000, 10000,100000 respectively.

Table 3. results of proposed model

Figure 3. false alarm versus signal to noise ratio for different values of N

As shown in figure 3 there is an inverse relation between the value of  and the signal to noise ratio, when N = 1000 then  = 0.03 at SNR = −10 dB and  = 0.85 at SNR = −20 dB. When N = 10,000 then  = 0 at SNR = −10 dB and  = 0.61 at SNR = −20 dB. When N = 40,000 then  = 0 at SNR = −10 dB and  = 0.24 at SNR = −20 dB. When N = 100,000 then  = 0 at SNR = −10 dB and  = 0.03 at SNR = −20 dB.

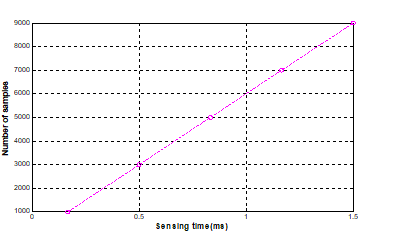
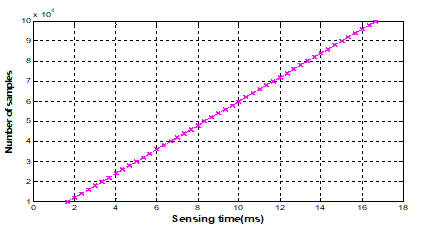
Figure 4. shows the graph of spectrum sensing time versus Number of samples from 1000 to 10000

Figure 5. Shows the graph of spectrum sensing time versus Number of samples from 10000 to 100000

As targeted in IEEE 802.22 standards that the time taken by CR users during the detection of PU spectrum bands for SS should be as small as possible. Figures 4, 5 show graphs of mean detection time of the proposed model versus various values of samples. As shown it is clear that the detection time increases with the increase of samples and these results are arranged at table 4 which shows that the proposed model take better time than other two stage techniques in table [1,2] .

Table 4. the proposed model sensing time for different values of N

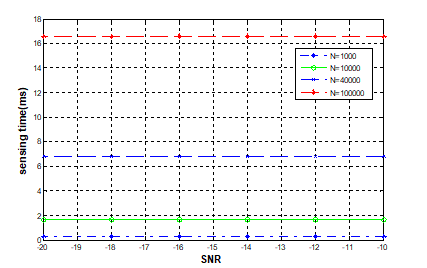
Figure 6. shows the graph of Sensing time versus SNR for different values of N

Finally, figure 6 shows the graph of Sensing time versus SNR for different values of N, From the Figure it is clear that the detection time increases with the value of N but the detection time will be less than the other two stage techniques in table [1, 2].

5. CONCLUSION

An improved spectrum sensing model and its performance evaluation are introduced in this paper. In this paper, a new model is discussed using IDD and ED technique to improve the different spectrum sensing parameters. The interval dependent de-noising technique is applied in the first stage to improve the reconstruction of the required signal in order to reduce the noise effect and to detect the PU signals accurately which make the proposed model achieves the desired target  and reduces  especially at low SNR as well as reduced sensing time compared to previous two stage sensing detector, The Simulation results of this method are utilized to demonstrate the reduction in sensing time. The obtained results demonstrated that the proposed model using IDD-ED is very better in terms of sensing time and false alarm. Different SNR values are taken to calculate the sensing time and probability of false alarm. The simulation results declared that the proposed model achieved alow  probability of false alarm and minimum sensing time.

STATEMENTS AND DECLARATIONS

• Funding: no funding was received to assist with the preparation of this manuscript.
• Financial interests: The authors declare they have no financial interests.

The authors have no competing interests to declare that are relevant to the content of this article.

• Consent to participate: not applicable

CONFLICTS OF INTEREST

The authors declare no conflict of interest.

REFERENCES
[1] FCC, Second report and order and memorandum opinion and order, ET Docket No. 08-260, 2008.

[2] Li, C., 2009.Department of Electronic Engineering, School of Electronic, Information and Electric Engineering,Shanghai Jiao Tong University, Report.Retrievedfrom:http://iwct.sjtu.edu.cn/ Personal/xwang8/research/CR_zhu/project.html.

[3] Khobragade, A. S., & Raut, R. D. (2017). Hybrid spectrum Sensing method for cognitive radio. International Journal of Electrical and Computer Engineering (IJECE), 7(5), 2683. https://doi.org/10.11591/ijece.v7i5.pp2683-2695.

[4] Yue, W. and B. Zheng, 2009. A two-stage spectrum sensing technique in cognitive radio systems based on combining energy detection and one-order cyclostationary feature detection. Proceeding of the International Symposium on Web Information Systems and Applications (WISA’09). Nanchang, P.R. China, pp: 327-330.

[5] I. F. Akyildiz, W.-Y. Lee, M. C. Vuran and S. Mohanty, Next generation/dynamic spectrum access/cognitive radio wireless networks: A survey, Computer Networks, vol.50, no.13, pp.2127- 2159, 2006.

[6] J. Ma, G. Li and B. H. Juang, Signal processing in cognitive radio, Proc. of the IEEE, vol.97, no.5, pp.805-823, 2009.

[7] T. Yucek and H. Arslan, A survey of spectrum sensing algorithms for cognitive radio applications, IEEE Communications Surveys Tutorials, vol.11, no.1, pp.116-130, 2009.

[8] S. Haykin, Cognitive radio: Brain-empowered wireless communications, IEEE Journal on Selected Areas in Communications, vol.23, no.2, pp.201-220, 2005.

[9] A. Fehske, J. D. Gaeddert and J. H. Reed, A new approach to signal classification using spectral correlation and neural networks, Proc. of IEEE DySPAN, pp.144-150, 2005.

[10] Z. Liu and J. Wang, A Hermitan mapping approach to unitary root-music algorithm for cyclostationary signals, International Journal of Innovative Computing, Information and Control, vol.5, no.10(A), pp.3123-3132, 2009.

[11] W. Yue and B. Zheng, Spectrum sensing algorithms for primary detection based on reliability in cognitive radio systems, Journal of Compute and Electrical Engineering, vol.36, no.3, pp.469-479, 2010.

[12] W. Yue, B. Zheng, Q. Meng and W. Yue, Combined energy detection and one-order cyclostationary feature detection techniques in cognitive radio systems, The Journal of China Universities of Posts and Telecommunications, vol.17, no.4, pp.18-25, 2010.

[13] I. F. Akildiz, B. F. Lo and R. Balakrishan, Cooperative spectrum sensing in cognitive radio networks: A survey, Physical Communication, vol.4, pp.40-62, 2011.

[14] I. W. G. on Wireless Regional Area Networks (WRANs), http://www.ieee802.org/22/.

[15] C. R. Stevenson, C. Cordeiro, E. Sofer and G. Chouinard, Functional requirements for the 802.22 WRAN standard, IEEE 802.22 Draft, 2005.

[16] K. Srisomboon, K. Thakulsukanant, A. Prayote, and W. Lee, “Adaptive two-stage spectrum sensing under noise uncertainty in cognitive radio networks,” ECTI Transactions on Electrical Engineering, Electronics, and Communications, vol. 14, no. 1, pp. 21-35, 2016.

[17] A. Ghasemi and E. S. Sousa, Spectrum sensing in cognitive radio networks: Requirements, challenges and design trade-offs, IEEE Communication Magazine, pp.32-39, 2008.

[18] Maleki, S., Pandharipande, A., & Leus, G. (2010, March). Two-stage spectrum sensing for cognitive radios. In 2010 IEEE International Conference on Acoustics, Speech and Signal Processing (pp. 2946-2949). IEEE.

[19] Bagwari, A., & Tomar, G. S. (2013). Two-stage detectors with multiple energy detectors and adaptive double threshold in cognitive radio networks. International Journal of Distributed Sensor Networks, 9(8), 656495.

[20] Ejaz, W., Hasan, N. U., & Kim, H. S. (2012). SNR-based adaptive spectrum sensing for cognitive radio networks. Int. J. Innov. Comput. Inf. Control, 8(9), 6095-6106.

[21] Geethu, S., & Narayanan, G. L. (2012). A novel high speed two stage detector for spectrum sensing. Procedia Technology, 6, 682-689.

[22] Bagwari, A., Kanti, J., Tomar, G. S., & Samara, A. (2016). A robust detector using snr with adaptive threshold scheme in cognitive radio networks. International Journal of Signal Processing, Image Processing and Pattern Recognition, 9(5), 173-186.

[23] Minny Bhola , Rinkoo Bhatia , Shruti Tiwari ,”Two Stage Spectrum Sensing for Cognitive Radio using Cyclostationarity detection and Energy Detection” International Journal of Latest Trends in Engineering and Technology (IJLTET) Vol. 1 Issue 4 November 2012.

[24] Kanti, J., & Tomar, G. S. (2018). Solution of sensing failure problem: an improved two-stage detector. The Computer Journal, 61(6), 847-855.

[25] Nair, P. R., Vinod, A. P., & Krishna, A. K. (2011, September). A fast two stage detector for spectrum sensing in cognitive radios. In 2011 IEEE.

[26] Rabie Mohamed, A., A. Aziz El-Banna, A., & A. Mansour, H. (2021). Multi-path hybrid spectrum sensing in cognitive radio. Arabian Journal for Science and Engineering, 46, 9377–9384.

[27] Rioul, O., & Vetterli, M. (1991). Wavelets and signal processing. IEEE signal processing magazine, 8(4), 14-38.

[28] Mallat, S. G. (1989). A theory for multiresolution signal decomposition: the wavelet representation. IEEE transactions on pattern analysis and machine intelligence, 11(7), 674-693.

[29] Teolis, Anthony, and John J. Benedetto. Computational signal processing with wavelets. Vol. 182. Boston, MA, USA: Birkhäuser, 1998.

[30] Mittermayr, C. R., Nikolov, S. G., Hutter, H., & Grasserbauer, M. (1996). Wavelet denoising of Gaussian peaks: a comparative study. Chemometrics and Intelligent Laboratory Systems, 34(2), 187-202.

[31] Donoho, D. L. (1995). De-noising by soft-thresholding. IEEE transactions on information theory, 41(3), 613-627.

[32] Alsberg, B. K., Woodward, A. M., & Kell, D. B. (1997). An introduction to wavelet transforms for chemometricians: A time-frequency approach. Chemometrics and intelligent laboratory systems, 37(2), 215-239.

[33] Walczak, Beata, ed. Wavelets in chemistry. Elsevier, 2000.

[34] Ghasemi, A., & Sousa, E. S. (2005, November). Collaborative spectrum sensing for opportunistic access in fading environments. In First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2005. DySPAN 2005. (pp. 131-136). IEEE.‏