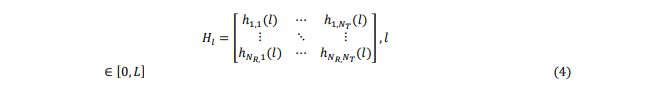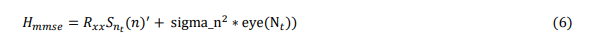IJCNC 05

CHANNEL ESTIMATION IN MIMO OFDM SYSTEMS
WITH TAPPED DELAY LINE MODEL
Ravi Hosamani1
, Yerriswamy T2
1Department of Electronics and Communication Engineering,K.L.E . Institute of
Technology, Hubballi, Karnataka, India 580027
2Department of Computer Science and Engineering. K.L.E. Institute of Technology
Hubballi, Karnataka, India 580027

ABSTRACT

The continuous increase in the user demands fornew-generation communication systems, is making the wireless channel more complex and challenging for estimation, developing a simulation model for the channel,and evaluating the performance of different MIMO systems. In this work, a simulation modelfor multipath fading channels in wireless communication is performed. The model includes a selection of typical Tapped-Delay-Line channel models that can be implemented to reproduce the effects of representative channel distortion and interference. Based on the simulation results, the proposed method
exhibits accurate channel estimation performance for frequency-selective fading channels. The proposed work employed LS, MMSE, and ML methods for channel estimation, using 16 and 32 pilots and fixed pilot locations in each frame. Results are obtained for 4×4, 8×8, 16×16, 16×8, and 16×4 MIMO systems andtapped delay line systems.

KEYWORDS

Channel estimation, MIMO systems, multipath fading, tapped-delay line, Mean square error

Introduction

In the generation of mobile networks, the latest standard for wireless communication have evolved substantially over the years. Current and future networks is to provide improved data transfer speeds, reduced latency, and increased capacity compared to the preceding generations of mobile networks[1]. These features are achieved through various advanced technologies like, Multiple antenna technology, network slicing to deliver faster and more reliable connectivity [2] mm wave frequencies. 5G networks are supposed to play a pivotal role in industrial internet of things (IIoT) which supports continuous connectivity to large number of devices with minimum latency and higher reliability. The 5G technology in combination with Industry 4.0 can bring a huge transformation across industries, enabling better productivity, efficiency and advanced automation [3, 4]. This makes a highly precise and efficient manufacturing as well as constructive monitoring and control of equipment and systems [5].

The attractive features of 5G, comes with various challenges while implementing them. These challenges are present at various levels or stages of communication systems. At physical layer, modulation schemes at higher frequencies and impact of channel state on the data transmitted using these techniques are the main thing which need to consider [6]. Various researchers are exploring the effect of these modulation schemes and channel behavior. Based on the observations, it is found that if channel state/behavior is previously known for certain scenario, effective communication can be achieved. In these systems, advanced techniques such as beamforming, massive MIMO, and network slicing heavily rely on accurate channel knowledge in order to achieve high spectral efficiency and reliable communication [7].

Channel estimation is the process of estimating the characteristics of a communication channel between a two points [8]. In wireless communication systems, channel estimation is essential to optimize the transmission parameters and improve the quality of the communication [9].Channel estimation can be done using various techniques, including pilot-based methods, blind estimation, and channel prediction. Pilot-based methods involve transmitting pilot symbols, along with the data symbols. These are used to estimate the channel behavior which includes the frequency response, phase, and delay spread [10]. This information can then be used to optimize the transmission parameters, such as the modulation scheme, coding rate, and transmit power. Blind estimation, on the other hand, involves estimating the channel characteristics without using any known reference signals. This can be done using statistical techniques, such as maximum likelihood estimation or least squares estimation, based on the received data symbols [11].

The motivation for the work is the need for accurate channel estimation in wireless communication systems. As the user demands for new communication systems, wireless channels become more complex and challenging for estimation. The objective of the work is to develop a simulation model for multipath fading channels in wireless communication that can accurately estimate the channel parameters. The contribution of the work is the proposed simulation model that includes typical Tapped-Delay-Line channel models, can be used to reproduce the effects of channel distortion and interference. The simulation results show that the proposed system can accurately estimate channel parameters for frequency-selective fading channels using LS, MMSE, and ML methods. Additionally, tested the system using various MIMO systems and tapped delay line systems to show its flexibility and applicability.

The article is organized into six chapters. The first chapter provides an introduction to the topic and the significance of channel estimation in wireless communication systems. The second chapter discusses the relevant literature on channel estimation and classical techniques that have been developed over the years. The third chapter presents the proposed system and channel models, including a discussion of the channel impulse response and its computation. The fourth chapter focuses on the implementation of the Channel Estimator (CE), discussing the various classical techniques used in channel estimation. The fifth chapter presents the simulation results and analysis of the proposed system, including a discussion of their implications. The sixth chapter provides a summary of the key findings of the study, limitations of the proposed system, and recommendations for future research. Finally, the reference section contains a list of all the sources cited in the article.

2.RELATED WORK

Y. Song et al. has proposed a channel estimation algorithm for MIMO-OFDM systems in timevarying channels. The algorithm uses a time-domain training sequence that considers correlation between antennas and subcarriers into account. Channel estimation is achieved through maximum likelihood estimator and Kalman filter to track the time-varying channels. The method is tested with existing algorithms, namely, the LS and the MMSE estimator. Results show that the proposed algorithm outperforms the existing algorithms in terms of mean square error and bit error rate. [12].

Y. Wang et al. proposed a low-complexity channel estimation algorithm for MIMO-OFDM systems. The algorithm utilizes the inherent sparsity of the channel impulse response (CIR) to reduce the number of pilot symbols required for accurate channel estimation. The algorithm consists of two stages: 1) sparse CIR estimation using a Bayesian compressive sensing algorithm and 2) CIR interpolation using a low-complexity Kalman filter. Results reveal that the proposed algorithm outperforms the conventional LS and LMMSE channel estimation methods in terms of both mean squared error (MSE) and bit error rate (BER) under various channel conditions. Moreover, the proposed algorithm is shown to achieve comparable performance to the computationally intensive AMP algorithm while requiring significantly lower complexity [13]. Z. Shen et al., proposed a new channel estimation method for MIMO-OFDM systems in timevarying frequency-selective channels. The method uses a combination of a deep neural network (DNN) and a channel prediction algorithm to estimate the channel. The DNN is used to extract the channel features from the pilot signals, and the channel prediction algorithm predicts the channel in the data transmission phase. The method was compared to several existing methods, including the least squares (LS) method and the minimum mean square error (MMSE) method. The study concludes that the proposed method is a promising solution for channel estimation in MIMO-OFDM systems in time-varying frequency-selective channels [14].

Y. Cai et al., proposed a joint pilot decontamination and channel estimation algorithm for massive multiple-input multiple-output (MIMO) orthogonal frequency-division multiplexing (OFDM) systems in frequency-selective fading channels. The algorithm uses a low-rank matrix completion (LRMC) method to eliminate the effect of pilot contamination and a sparse Bayesian learning (SBL) algorithm to estimate the frequency-selective channel [15].

Rezaeiet.al., proposed a novel low-overhead channel estimation technique for frequency-selective multiple-input multiple-output (MIMO) systems. The method employs a differential evolution algorithm (DEA) to optimize the pilot pattern and estimate the channel response. The DEA-based approach can efficiently estimate the channel in time-varying environments and alleviate pilot contamination issues in MIMO systems. The method achieves high estimation accuracy with a lower pilot overhead than conventional techniques, making it more efficient for practical applications [16].

Ashraf et al. proposed a new frequency-selective channel estimation technique for 5G communication systems. The method utilizes a sparse Bayesian learning (SBL) algorithm to estimate the channel response in frequency-selective environments. The method is evaluated using numerical simulations, and the results show that the SBL-based approach can achieve higher accuracy in estimating the channel response compared to other existing methods. Also, the method reduces the pilot overhead and enhance the spectral efficiency of the 5G system. The authors also provide a comprehensive analysis of the performance of the proposed method under different scenarios, such as different channel conditions, Doppler frequencies, and channel coherence times [17].

H. Zhou, et.al., proposed a low-complexity channel estimation algorithm for OFDM-based cooperative communication systems. The algorithm is based on the pilot-aided least squares (PALS) algorithm, which uses the pilot symbols transmitted by the source and relay nodes to estimate the channel frequency response. The algorithm uses a low-complexity scheme to reduce the number of required pilot symbols, which is achieved by dividing the pilot symbols into groups and using them in a cyclic manner. The algorithm provides a practical solution for lowcomplexity channel estimation in OFDM-based cooperative communication systems, which can effectively reduce the overhead of pilot symbols and improve the system performance [27].

3.SYSTEM AND CHANNEL MODELS

Wireless systems performance evaluation typically involves modeling or emulating the physical radio channel. The enormous evolution is seen in channel models due to increase complexity and various amendments and user demands in communication systems. The Channel Impulse Response (CIR) contains crucial details about a channel that enable the examination of any wireless transmission that traverses it. This is because, under certain circumstances, the radio channel can be modeled as a linear filter. Eq (1) [18] can be employed to express the timevarying impulse response of the multipath channel in baseband. This involves computing the amplitudes and time delays of multiple waves that arrive at distinct intervals and adding them up to derive the CIR.

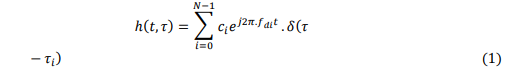
At the receiver, every path i has an amplitude of ci, a delay of τi, and a Doppler shift of fdi. The Doppler shift arises due to the motion of the mobile station and environmental changes, causing a change in the frequency of the radio signal. The amount of Doppler shift is proportional to both mobile speed and carrier frequency. The difference between the maximum and minimum frequency shifts resulting from multipath is referred to as frequency spread. Depending on the statistical distribution of the angle of arrival in each path. The CIR can be expressed using simple Tapped-Delay-Line (TDL) or Cluster-Delay-Line (CDL) models [19]. More advanced models and the latest trends in channel models fund in [20-23].

The TDL (tap delay line) model characterizes the wireless channel between a transmitter and receiver by using statistical parameters, rather than incorporating the physical layout of the environment. This model represents the time-domain CIR as a series of discrete taps, where each tap has its own time-varying amplitude, delay, and coefficient values, as shown in eq(2)

The tap in the wireless channel is modeled as a Dirac delta function, and the overall time-varying channel impulse response h (t, τ) is represented as a sum of delayed taps. The model assumes that there are N paths in the channel, where ci(t) is a complex amplitude coefficient that varies with time, δ is the Dirac delta function, and τi represents the delay of the ith path. Each tap is associated with a Doppler spectrum that determines how the coefficients change over time.

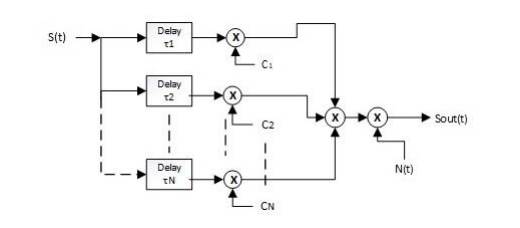
The proposed model defines the channel impulse response as a finite sum of taps, which is restricted by a maximum of N paths. The separation between two adjacent paths is dependent on the system’s bandwidth, and if the coefficients ci are stable, eq (3) can be utilized to express the output signal of the channel. The block diagram of a tapped-delay channel model as shown in Figure.1 illustrates components signal flow. The input signal represents the transmitted signal in the wireless communication system. It can be a continuous-time analog signal or a discrete-time digital signal. Taps represent the individual delay paths in the channel model. Each tap represents a different propagation path or reflection, and it has associated attenuation and phase shift parameters. The number of taps corresponds to the number of multipath components or echoes considered in the model. Each tap is followed by a delay element that introduces a specific time delay corresponding to the propagation delay of the associated path. The delays account for the differences in arrival times of the multipath components. Attenuation elements are placed after the delay elements to scale the signal strength of each tap. The attenuation factor represents the loss or attenuation experienced by the signal in the specific propagation path. Phase shift elements introduce the phase shifts experienced by the signal due to the propagation path. These phase shifts are caused by differences in path lengths and reflections. The adders combine the delayed and scaled tap signals to produce the overall channel output. The channel output represents the received signal after passing through the tapped-delay channel model. It incorporates the effects of multipath propagation, including delays, attenuations, and phase shifts.

Figure 1. Block diagram of a tapped-delay channel model

However, not all of the models are suitable for real-time physical emulation and to ensure accurate and reliable emulation, it is necessary to have specific information about the channel. Therefore, in this study, we have chosen a TDL-based model that provides a detailed description of the channel in each scenario. Consider the MIMO channel that experiences frequency-selective block fading. The channel has L + 1 tap discrete-time channel impulse response (CIR) denoted as 𝐻 = 𝐻1, 𝐻2 − −, 𝐻𝐿−1, 𝐻𝐿 and it involves 𝑁𝑇 transmitters and 𝑁𝑅 receivers.

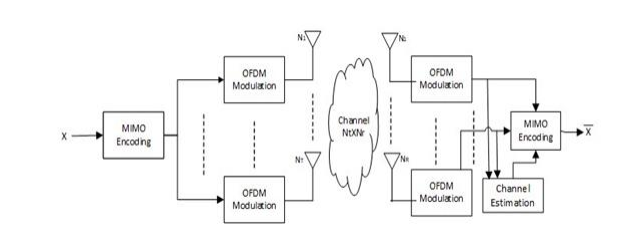
A block diagram of a MIMO (Multiple-Input Multiple-Output)OFDM (Orthogonal Frequency Division Multiplexing) system represents the structure and signal flow of a communication system that utilizes multiple antennas at both the transmitter and receiver, combined with OFDM modulation as shown in Figure. 2 the Source Signals: Multiple source signals or data streams are generated from different sources or data inputs. The source signals are then processed by a MIMO encoder, which combines them with appropriate weights and spatial multiplexing techniques to exploit the spatial diversity provided by multiple antennas at the transmitter [35]. The processed signals are then modulated using OFDM, which converts the data streams into parallel subcarriers. An Inverse Fast Fourier Transform (IFFT) is applied to each subcarrier to convert the frequency domain symbols into time-domain OFDM symbols. A cyclic prefix (CP) is added to each OFDM symbol to mitigate the effects of multipath interference. : Known pilot symbols are inserted into the transmitted OFDM symbols at regular intervals. The transmitted OFDM symbols propagate through a wireless channel, which introduces fading, multipath effects, and noise.

In a MIMO system, the wireless channel consists of multiple paths with different gains and phases for each transmit-receive antenna pair [35]. At the receiver, the CP is removed from each OFDM symbol.The received pilot symbols are used to estimate the channel conditions, including channel gains, phases, and other parameters. The estimated channel information is interpolated or extrapolated to obtain channel estimates for the entire OFDM symbol.The estimated channel parameters are used to construct the channel matrix, which describes the relationship between transmitted and received signals in a MIMO system. A Fast Fourier Transform (FFT) is applied to each OFDM symbol to recover the frequency domain representation. The received signals from multiple receive antennas are processed by a MIMO decoder, which separates and extracts the transmitted data streams using spatial processing techniques. Each separated data stream may undergo channel decoding to correct errors introduced during transmission. The channel-decoded signals are further processed to recover the original source signals. The recovered source signals represent the reconstructed data streams at the receiver’s output[36].

Figure 2. MIMO OFDM System

In a MIMO OFDM system, the data (X) is transmitted simultaneously over multiple subcarriers using orthogonal frequency division multiplexing. The subcarriers are orthogonal to each other, which reduces the interference between them and allows more data to be transmitted over the same bandwidth.

Consider that there are NT transmit antennas and NR receive antennas as shown in fig 2, the channel matrix can be represented as eq (4). Each element Hl= hijrepresents the complex channel gain between the ith transmit antenna and the jth receive antenna.

Channel estimation is necessary to estimate the frequency response of the multiple channels between each transmit and receive antenna pair. The channel estimation process in MIMO OFDM systems. Pilot symbols are transmitted from each transmit antenna to each receive antenna.The pilot symbols are usually arranged in a grid pattern, called a pilot matrix that spans the frequency-time grid of the OFDM symbols. The cyclic prefix 𝐶𝑃𝑛𝑡 is used to separate the data and training symbols in the training sequence transmitted by the 𝑛𝑖 𝑡ℎ antenna. The length of 𝐶𝑃𝑛𝑡 is set to L, and it is defined as [𝑆𝑛𝑡 (𝑁𝑠 − 𝐿), . . . , 𝑆𝑛𝑡(𝑁𝑠 − 1)], where 𝑆𝑛𝑡represents the transmitted signal and 𝑁𝑠is the total number of samples in the signal. The received training signal on 𝑁𝑅 receive antennas. The pilot symbols are designed to be orthogonal to each other and to the data symbols, so that they can be easily distinguished at the receiver as shown in Fig 2. The received pilot symbols are used to estimate the channel frequency response for each transmit-receive antenna pair. There are several methods for channel estimation in MIMO OFDM systems. The vector [𝑦1 (𝑛), 𝑦2 (𝑛) − − − − − −𝑦𝑁𝑅(𝑛)]′represents the signals received by 𝑁𝑅 receive antennas at time n, while the complex noise matrix is denoted as E and defined as 𝐸 = [𝑒(0), 𝑒(1),· · · , 𝑒(𝑁𝑠 − 1)], where e(n) is the vector of additive noise components for each receive antenna, i.e 𝑒(𝑛) = [𝑒1 (𝑛), 𝑒2 (𝑛), − − −𝑒𝑁𝑅 (𝑛) ]′ It is important to note that 𝑆𝑛𝑡 (𝑛) represents the pilot symbol transmitted by the 𝑛𝑡ℎ
transmit antenna at time n, 𝑦𝑛𝑟 (𝑛) represents the signal received by the 𝑛 𝑡ℎ receive antenna at time n, 𝑒𝑛𝑟 (n) represents the additive noise component in 𝑦𝑛𝑟 (𝑛)and the expected signal-to-noise ratio (SNR) on each receive antenna is calculated for n ∈ [0, Ns−1]. The use of multiple antennas at the transmitter and receiver sides allows the system to use spatial diversity, which means that the signals transmitted from different antennas can take different paths to the receiver, reducing the effects of fading and improving the reliability of the system.

4.CHANNEL ESTIMATION (CE)

This section discusses the implementation of the Channel Estimator (CE), a fundamental component in wireless communication systems that aids in the recovery of transmitted data by estimating the state of the channel through which the data travels. Effective implementation of the CE can significantly improve the reliability and accuracy of the received signals, enabling better performance of the communication system as a whole.

Channel estimation is essential for reliable communication and plays a critical role in the performance of the overall communication system. Classical channel estimation techniques have been extensively researched and developed over the years, and this section will discuss some of these classical techniques in detail. These techniques include Least Squares (LS), Maximum Likelihood (ML), Minimum Mean Square Error (MMSE), Understanding these techniques is vital for effectively implementing channel estimation in wireless communication systems

LS (Least Squares) estimation is a method for estimating the unknown parameters of a mathematical model by minimizing the sum of the squares of the differences between the predicted values of the model and the actual observations [24]. It is a popular method in many fields, including statistics, signal processing, and machine learning. In the context of wireless communication, LS estimation can be used to estimate the channel response in a communication system [25]. The LS estimate of the channel response is obtained by minimizing the sum of the squared errors between the received signal and the predicted signal, using the estimated channel response [26]. Specifically, the LS estimate of the channel response eq (5)

𝐻𝑙𝑠is the LS estimate of the channel response, Y is the received signal, X is the transmitted signal (known training symbols), and ‘ denotes the conjugate transpose. The LS estimate is simple to compute and is commonly used in many communication systems, although it is sensitive to noise and may not be optimal in some situations channel estimation and equalization using the least squares error (LSE) method followed by zero-forcing (ZF) equalization[27].

The input variables to the are: The input are received symbols, pilot which is a pilot sequence, positions of the pilot subcarriers, the number of transmit and receive antennas, the number of subcarriers, number of channel taps, the noise variance. The input variables to the are: estimated channel impulse response, estimated frequency response of the channel, then performs equalization by looping over each subcarrier and calculating the inverse of the estimated channel frequency response using the Moore-Penrose pseudoinverse of a matrix. The resulting equalized symbols are stored in the variable.

MMSE (Minimum Mean Square Error) estimation is a method for estimating the unknown parameters of a mathematical model by minimizing the expected value of the squared difference between the predicted values of the model and the actual observations [28]. It is a popular method in many fields, including signal processing, control theory, and machine learning. MMSE estimation can be used to estimate the channel response in a communication system [29].The MMSE estimate of the channel response is obtained by minimizing the expected value of the squared error between the received signal and the predicted signal, using the estimated channel response [30]. Specifically, the MMSE estimate of the channel response is given byeq (6):

Where 𝐻𝑚𝑚𝑠𝑒the MMSE estimate of the channel response is, 𝑅𝑥𝑥 is the autocorrelation matrix of the known training symbols𝑆𝑛𝑡 (𝑛), sigma 𝑛 2 is the noise variance, and eye(𝑁𝑡 matrix of size 𝑁𝑡𝑥𝑁𝑡 in eq (4). The MMSE estimate takes into account the noise in the received signal and is generally more robust to noise than the LS estimate [31]

The MMSE method offers advantages over LS and ML methods by providing improved performance in noise, low-SNR scenarios, multipath fading environments, and achieving an optimal trade-off between bias and variance in channel estimation.

Implement channel estimation and equalization using the minimum mean squared error (MMSE) algorithm. Input are same as used for LS estimation, the output is the estimated channel is the frequency response of the estimated channel. The equalization with MMSE is performed in the following loop by computing the pseudo-inverse of the matrix H’ * H + N0 * eye(Nt) ,the estimated channel frequency response for each subcarrier, and N0 is the noise variance. The result is multiplied by the received symbols to obtain the equalized symbols. The mean squared error (MSE) between the equalized symbols and the original transmitted symbols is computed and stored.

Maximum likelihood (ML) based channel estimation is a method used in communication systems to estimate the channel coefficients of a communication channel. In this method, the receiver uses the maximum likelihood principle to estimate the channel coefficients based on the received signal [32]. The ML-based channel estimation assumes that the transmitted signal is known, and the receiver measures the received signal at different time intervals. The received signal is modelled as a linear combination of the transmitted signal and the channel coefficients, with additive noise. The goal of the ML-based channel estimation is to estimate the channel coefficients that maximize the likelihood function of the received signal [33].

To perform ML-based channel estimation, the receiver first constructs a likelihood function that describes the probability of the received signal given the channel coefficients. The likelihood function is usually expressed in terms of the channel coefficients and the received signal. The receiver then computes the maximum of the likelihood function to obtain the estimated channel coefficients implement channel estimation and equalization using the maximum likelihood (ML) algorithm [34]. Input is same as used for LS estimation. It initializes and loops over all subcarriers. For each subcarrier, it extracts the estimated channel coefficients H, and the received symbols and computes the ML estimate of the transmitted symbol for that subcarrier using the minimum distance criterion. The ML estimate is stored in the corresponding variable. Finally, it computes the mean squared error (MSE) between the estimated symbols and the transmitted symbols, and stores the result in the variable.

5.SIMULATION AND DISCUSSION

In the simulation 2 and 4 taps in each sub channel ℎ𝑛𝑡𝑛𝑟𝑁𝑇= 4,8,16, 𝑁𝑅 = 4, 8, and N = 64,128 for the, additive noise, we assume elements of E are white complex Gaussian with unit variance. For the underlying fading channel, Elements of H are independent complex Gaussian, These parameters help to identify the performance of channel estimation with respect to SNR as shown in table I.

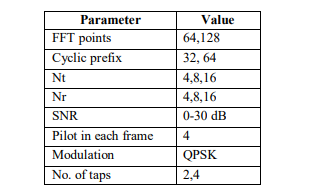
Table 1. Simulation parameters

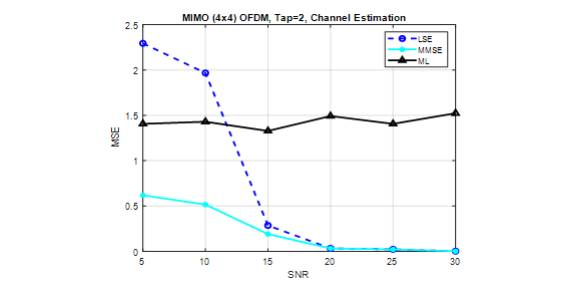
The result compares channel estimation using the LS and MMSE techniques, employing 16 pilots for channel estimation in each frame for MIMO 4×4. According to the results presented in Figure.3, the LS method performs poorly at lower SNRs, at SNR=10, MSE of LS=2 while the MMSE=0.5 method exhibits superior performance, the ML method demonstrates MSE as 1.3.

Figure 3. CE of MIMO (4×4), tap=2, pilots=16

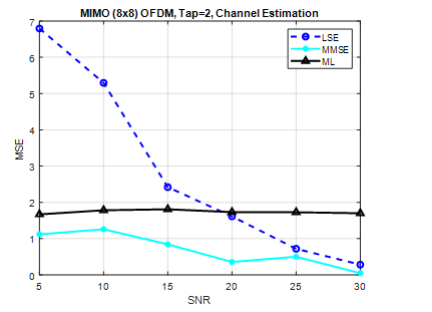
The channel estimation in MIMO 8×8 systems, with pilots=32 is shown in Figure.4. The LS method performs worse at lower SNRs, at 10dB its power of MSE=0.5 while the MMSE method outperforms as MSE is 1.3. Furthermore, the ML method displays nearly constant MSE it is around 1.8.

Figure 4.CE of MIMO (8×8), tap=2, pilots=32

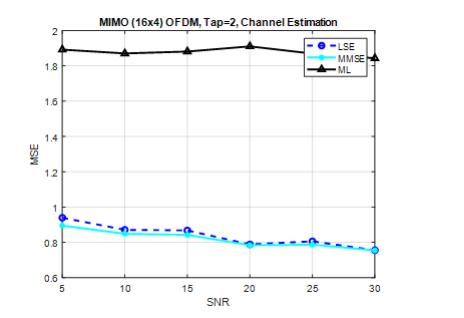
Figure.5 shows the channel estimation in MIMO 16×4 systems with pilots=32. The LS method and the MMSE perform almost similar at SNR=10dB, it is power of MSE is .084 and 0.82 respectively. In addition, the ML method demonstrates almost constant MSE of 1.3 to 1.5 for different SNR

Figure 5. CE of MIMO (16×4), tap=2, pilots=32

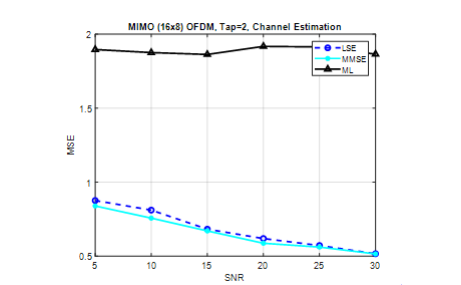
Figure 6. CE of MIMO (16×8), tap=2, pilots=32

In Figure.6, presents channel estimation of MIMO 16×8 systems with 32 pilots for channel estimation in each frame. The results demonstrate that the LS and MMSE methods perform similarly at higher SNR at 20dB, exhibiting little difference in performance. Additionally, the ML method shows nearly constant MSEpower around 1.8 To 1.9 MSE.

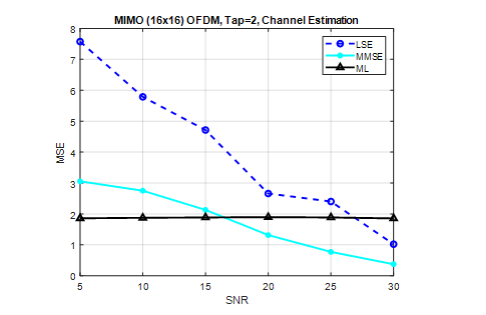
Figure 7. CE of MIMO (16×16), tap=2, pilots=32

In this study, we evaluated the performance of LS and MMSE techniques for channel estimation in MIMO 16×16 systems, using pilots=32 with tap=2 for channel estimation in each frame. Our analysis, as illustrated in Figure.7, indicates that the LS method underperforms at lower SNRs compared to the MMSE method at SNR =10dB, MSE power is 8 and 3, the ML method shows consistent MSE throughout the evaluation 1.9 of MSE power.

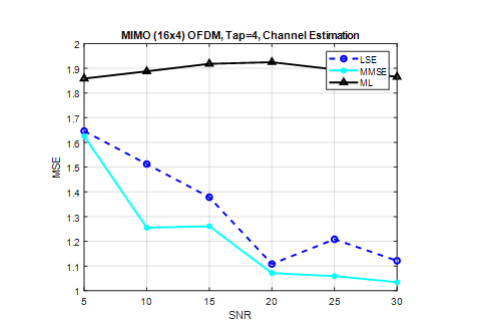
Figure 8. CE of MIMO (16×4), tap=4, pilots=32

The purpose of our investigation was to compare the effectiveness of LS and MMSE techniques in channel estimation MIMO 16×4 systems, utilizing 32 pilots and a tap of 4 for channel estimation in each frame. Our findings, illustrated in fig. 8, demonstrate that the LS method performs less optimally than the MMSE method at lower SNRs at SNR=10dB, power of MSE is 1.2 and 1.5 respectively. Which indicated increase number of tap effect on MSE which can analysed from Figure.

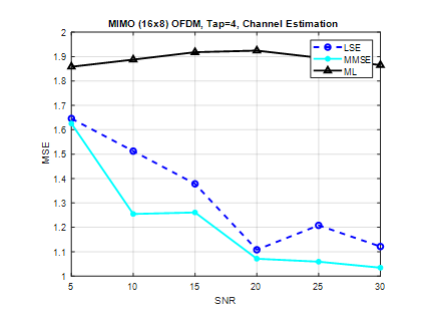
Figure 9. . CE of MIMO (16×8), tap=4, pilots=32

LS and MMSE techniques in channel estimation and detection for MIMO 16×4 systems, utilizing 32 pilots and a tap of 4 for channel estimation in each frame. Based on our results depicted in Figure. 9. Increase in tap in the systems, results indicates that the LS method performs sub-optimally at lower SNRs in comparison to the MMSE method at SNR=10dB, which demonstrates superior performance. Furthermore, the ML method maintains a consistent MSE throughout the evaluation as in Figure.9 and Figure.6.

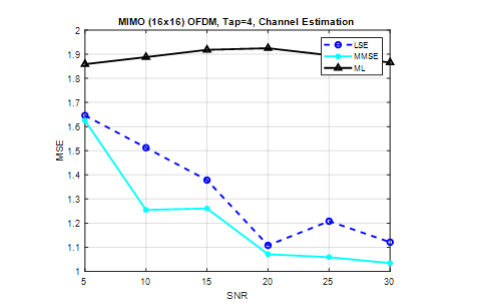
Figure 10. CE of MIMO (16×16), tap=4, pilots=32

The performance of LS and MMSE techniques for channel estimation and detection in MIMO 16×16 systems, using 32 pilots and a 4-tap channel estimation per frame, was evaluated. The results, presented in Figure.10 and Figure.7 indicate that the MMSE method outperforms the LS method at lower signal-to-noise ratios (SNRs) for increased tap numbers. Additionally, the ML method maintains a consistent mean squared error (MSE) across the evaluation of with different taps.

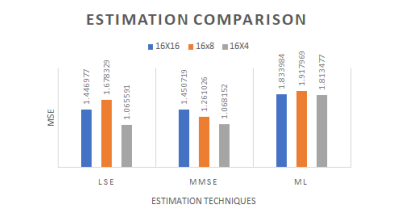
Figure 11. . MSE Vs MIMO (Nt, Nr), tap=2, pilots=32

Figure.11 depicts the MSE plotted against different antenna configurations in MIMO systems with 2-channel taps and 128 pilots, with a fixed SNR of 15dB. The results indicate that the LS method yields a higher MSE for the 16×16 MIMO system, whereas the MMSE method exhibits a lower MSE for the 16×8 MIMO system. In contrast, the ML method performs consistently across various MIMO sizes.

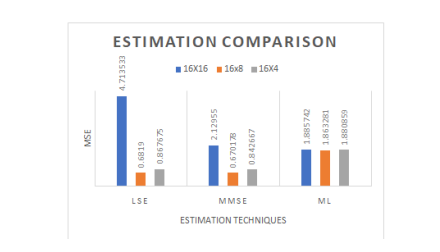
Figure 12. MSE Vs MIMO (Nt, Nr), tap=4, pilots=32

The MSE is plotted against different antenna configurations in MIMO systems with 4-channel taps and 32 pilots in Fig. 12, with a fixed SNR of 15dB. The outcomes show that the LS method results in a lower MSE for the 16×16 MIMO system than in Figure. 11. Conversely, the MMSE method yields a lower MSE for the 16×8 MIMO system compared to Figure.11. However, the ML method performs uniformly across various MIMO sizes and taps. From these results, we can see that MMSE method performs better over LSE and ML methods for almost all the scenarios. LSE method has higher MSE for lower SNRs, but as SNR increases it gives better performance nearly same as MMSE method. The ML estimation technique aims to find the parameter values that maximize the likelihood of the observed data given a specific model. In wireless communication systems, ML estimation takes into account the statistical characteristics of the
received signals and noise to estimate the channel parameters accurately. ML estimation is known to achieve the Cramer-Rao Lower Bound (CRLB) for parameter estimation, which represents the minimum variance attainable for unbiased estimators. It achieves the lowest possible estimation error in large sample sizes. ML estimation is optimal when the noise follows a Gaussian distribution, which is a common assumption in many wireless communication systems. In such cases, ML estimation provides the best estimate of the true channel parameters. ML method can be used in low SNR regimes or the scenarios where we have a fixed error tolerance as in all scenarios we receive nearly constant MSE in ML method.

6 . CONCLUSION

The continuously increasing demand in communication network is enforcing adaptive channel estimation techniques in current generation communication systems. In this paper, we present a simulation performance of communication channel for multipath fading scenarios in wireless communication. The model includes Tapped-Delay-Line channel models to reproduce the effects of channel distortion and interference. Based on the simulation results, it can be concluded that the proposed system is effective in accurately estimating the channel parameters that are subjected to frequency-selective fading. This work employs LS, MMSE, and ML methods for channel estimation and detection using 16, and 32 pilots and fixed pilots for channel estimation in each frame. The MMSE method given better MSE performance in all the scenarios. The LS method with specific configurations and taps exhibit small MSE for high-order antenna performance. However, the MMSE and ML methods consistently outperform the LS method in all configurations for both channel estimation in wireless communications system. The simulation results obtained from our study provide valuable insights and serve as a foundation for optimizing the performance of wireless communication systems in realistic channel environments. They aid in system design, algorithm development, performance evaluation, and optimization techniques, ultimately leading to improved system performance and efficiency so proposed simulation model and methods can be used for evaluating and optimizing the performance of wireless communication systems in realistic channel environments.

7.FUTURE WORK

This paper has examined classical estimation methods for different antenna array between transmitter and receiver with different tap delay line. The proposed simulation model and methods can indeed be applied to different types of wireless communication systems. While the specific implementation may require some adjustments or customization to suit the characteristics of the particular wireless system. However exact implementation and parameters may vary
depending on the specific system requirements, channel characteristics, and available resources. Some adaptations or modifications may be necessary to ensure optimal performance in different wireless communication scenarios. This study motivates the researchers to work on advanced channel estimation techniques machine learning-based approaches and implementing the proposed system in a real-world wireless communication system to identify and address practical
deployment challenges. These avenues for future research could help in advancing the field of wireless communication and improving the performance of wireless communication systems under various channel conditions.

CONFLICTS OF INTEREST
The authors declare no conflict of interest

ACKNOWLEDGMENT
The authors thank Visvesvaraya Technological University (VTU), Belagavi-590018, and K.L.E Institute of Technology, Hubballi-580027, for providing a platform to carry out the research work.

REFERENCE

[1] Aijaz, R. Gudipati, S. Muhaidat, and J. Rodriguez,(2017) “5G wireless networks: Opportunities and challenges,” Wireless Personal Communications, vol. 94, no. 2, pp. 795-823

[2] R. A. Shaikh, A. S. Sadiq, and S. Ahmed,(2019) “5G wireless networks: A comprehensive survey,”IEEE Communications Surveys & Tutorials, vol. 21, no. 3, pp. 2875-2902.

[3] P. Gupta and A. K. Singh,(2020) “5G-Enabled Industry 4.0: A Review” International Journal of Engineering and Advanced Technology, vol. 9, no. 1, pp. 3535-3541, A. Naseer, M. Hussain, and N. Javaid,(2021) “5G-Enabled Industry 4.0: A Survey on the Emerging Trends and Research Challenges” IEEE Access, vol. 9, pp. 90579-90591.

[4] S. Garg, S. Tyagi, S. Singh, and S. Singh,(2021) “Industry 4.0 Enabled by 5G Networks: AnOverview, Challenges, and Opportunities” IEEE Consumer Electronics Magazine, vol. 10, no. 4, pp.59-68, July 2021.

[5] H. Kim and J. Kim,(2020) “A Survey of 5G Communication Systems: Architecture, Radio Access, and Core Network,” Journal of Communications and Networks, vol. 22, no. 4, pp. 330-343. International Journal of Computer Networks & Communications (IJCNC) Vol.15, No.6, November 2023
112

[6] T. Li, Q. Zhang, and G. Li,(2021) “5G and Beyond: Recent Advances and Future Outlook,” IEEE Network, vol. 35, no. 1, pp. 8-15.

[7] R. Hosamani and T. Yerriswamy,(2022) “CSI based Performance Investigation of Single Cell-Multi user MaMIMO System,” 2nd Asian Conference on Innovation in Technology (ASIANCON), IEEE, 2022.A. J. Goldsmith(200), Wireless Communications. Cambridge University Press, 2005.

[8] G. Kaddoum and A. O. Boudraa, (2020) “Time-frequency based channel estimation techniques for OFDM-based systems: A survey,” Digital Signal Processing, vol. 97, pp. 102671

[9] S. Zhang and Y. Chen, (2021)”Channel estimation and performance analysis for wireless sensor networks in frequency-selective fading channels,” IEEE Access, vol. 9, pp. 17934-17946

[10] Y. Song and Y. Li,(2007) “Channel Estimation for MIMO-OFDM Systems in Time-Varying Channels,” in IEEE Transactions on Broadcasting, vol. 53, no. 4, pp. 884-892,doi: 10.1109/TBC.2007.908704.

[11] Y. Wang, L. Dai, Z. Wang, and S. Zhang, (2012)”A Low-Complexity Channel Estimation Algorithm for MIMO- OFDM Systems,” in IEEE Transactions on Wireless Communications, vol. 11, no. 9, pp. 3226-3235, doi: 10.1109/TWC.2012.072012.111243.

[12] Z. Shen et al.,(2019) “Channel Estimation for MIMO-OFDM Systems in Time-Varying FrequencySelective Channels,” IEEE Transactions on Vehicular Technology, vol. 68, no. 5, pp. 4589-4601, DOI: 10.1109/TVT.2019.2901674.”

[13] Y. Cai et al., (2019)”Pilot Decontamination and Channel Estimation for Massive MIMO-OFDM Systems in Frequency-Selective Fading Channels,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 4, pp. 898-912, DOI: 10.1109/JSAC.2019.2906802″

[14] M. H. Rezaei and S. S. Agaian(2021) “Low-Overhead Channel Estimation for Frequency-Selective MIMO Systems using Differential Evolution Algorithm” (IEEE Transactions on Communications).

[15] M. Ashraf, K. T. K. Teo, Y. Li, Z. Yang, and Y. Zhang, (2020) “Frequency Selective Channel 19, no. 2, pp. 1323-1335, DOI: 10.1109/TWC.2019.2956407.

[16] S. Salous,(2013) Radio Propagation Measurement and Channel Modelling.Hoboken, NJ, USA: Wiley

[17] A.F. Molisch, (2012)Wireless Communications, vol. 34, 2nd ed. Hoboken, NJ,USA: Wiley

[18] P. Almers, E. Bonek, N. Czink, M. Debbah, A. Burr, G. Matz, V. Degli-Esposti, H. Hofstetter, P. Kyösti, D. Laurenson, A. F. Molisch, C. Oestges, and H. Özcelik,(2007) “Survey of channel and radio propagation models for wireless MIMO systems,” EURASIP J. Wireless Commun. Netw., vol.
2007, no. 1, p. 19.

[19] P. Ferrand, M. Amara, S. Valentin, and M. Guillaud, (2016) “Trends and challenges in wireless channel modeling for evolving radio access,” IEEE Commun. Mag., vol. 54, no. 7, pp. 93_99

[20] Guidelines for evaluation of radio transmission technologies for IMT- 2000,” Int. Telecommun. Union, Geneva, Switzerland, Tech. Rep. Rec.ITU-R M.1225. Question ITU-R 39/8, 1997.

[21] Guidelines for evaluation of radio interface technologies for IMTadvanced,(2009)” Int. Telecommun. Union, Geneva, Switzerland, Tech. Rep. M.2135-0 (2008)

[22] P. Hong and Y. Hwang,(2020) “Low Complexity Channel Estimation for OFDM Systems using Least Squares Algorithm with Joint Spatial-Frequency Correlation Exploitation,” in IEEE Access, vol. 8, pp. 219580-219593, doi: 10.1109/ACCESS.2020.3047438.

[23] S. Chen, C. Yang, and Q. Liu,(2020) “Low-Complexity Channel Estimation Based on Recursive Least Squares Algorithm for OFDM Systems,” in IEEE Access, vol. 8, pp. 222444-222455, doi: 10.1109/ACCESS.2020.3049336.

[24] J. Liu, Y. He, H. Zhu, and X. Zhang,(2021) “Improved Channel Estimation for UFMC Systems Based on Variable Step Size Least Squares Algorithm,” in IEEE Access, vol. 9, pp. 44425-44436, doi: 10.1109/ACCESS.2021.3068419.

[25] H. Zhou, Y. Wang, and Q. Yang,(2021) “Low-Complexity Channel Estimation for OFDM-BaseCooperative Communication Systems using Pilot-Aided Least Squares Algorithm,” in IEEE Access, vol. 9, pp. 47674-47685, doi: 10.1109/ACCESS.2021.3067845.

[26] M. A. Elshennawy, A. El-Keyi, and A. K. Elmaghraby, (2019)”Channel estimation in MIMO-OFDM
systems using MMSE estimation technique,” in 15th International Computer Engineering Conference
(ICENCO), 2019, pp. 18-22.

[27] S. M. Hossain, M. S. Islam, and M. H. Rahman,(2019) “MMSE-based channel estimation for multiantenna systems with pilot contamination,” in IEEE International Conference on Advanced Communication Technologies and Networking (CommNet), pp. 1-5.

[28] X. Zhang, F. Jiang, and H. Liu,(2021) “Joint user activity detection and channel estimation for grantfree massive MIMO with MMSE,” in 2021 IEEE International Conference on Communications Workshops (ICC Workshops), pp. 1-6.

[29] K. N. Choudhury, M. A. Islam, and A. Bhattacharjee,(2022) “Adaptive MMSE Channel Estimation for Massive MIMO Systems,” in IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), pp. 1-5.

[30] Y. Zhao, X. Zhang, and M. Elkashlan, (2019)”Channel Estimation for Hybrid Millimeter Wave Massive MIMO Systems via Maximum Likelihood Estimation,” in 2019 IEEE Global Communications Conference (GLOBECOM), pp. 1-6.

[31] W. Li, H. Cao, and X. Li, (2021) “Joint Channel Estimation and Equalization for Underwater Acoustic OFDM Systems Using Maximum Likelihood Estimation,” in IEEE International Conference on Communications (ICC), pp. 1-6.

[32] S. A. Basit, S. A. Malik, and S. G. M. Amin, (2022)”A Maximum Likelihood Approach for Joint Estimation of DOA and Channel Parameters for Multipath Propagation,” in 2022 IEEE 17th Annual Wireless and Microwave Technology Conference (WAMICON), pp. 1-5.

[33] E. Stergiou, C. Angelis, and S. V. Margariti, “Evaluation Methodology of MIMO Networks Performance over Rayleigh Fading,” International Journal of Computer Networks & Communications (IJCNC), vol. 12, no. 1, pp. 37, January 2020, doi: 10.5121/ijcnc.2020.12103.

[34] P. Poornima, G. Laxminarayana, and D. Srinivas Rao, “Performance Analysis of Channel Capacity and Throughput of LTE Downlink System,” International Journal of Computer Networks & Communications (IJCNC), vol. 9, no. 5, pp. 55, September 2017, doi: 10.5121/ijcnc.2017.9505

AUTHORS