IJNSA 01

INVERTIBLE NEURAL NETWORK FOR
INFERENCE PIPELINE ANOMALY DETECTION

Malgorzata Schwab and Ashis Biswas
Department of Computer Science and Engineering, University of Colorado,at Denver, Colorado

Abstract

This study combines research in machine learning and system engineering practices to conceptualize a paradigm-enhancing trustworthiness of a machine learning inference pipeline. We explore the topic of reversibility in deep neural networks and introduce its anomaly detection capabilities to build a framework of integrity verification checkpoints across the inference pipeline of a deployed model. We leverage previous findings and principles regarding several types of autoencoders, deep generative maximum- likelihood training and invertibility of neural networks to propose an improved network architecture for anomaly detection. We hypothesize and experimentally confirm that an Invertible Neural Network (INN) trained as a convolutional autoencoder is a superior alternative naturally suited to solve that task. This remarkable INN’s ability to reconstruct data from its compressed representation and to solve inverse problems is then generalized and applied in the field of Trustworthy AI to achieve integrity verification of an inference pipeline through the concept of an INN-based Trusted Neural Network (TNN) nodes placed around the mission critical parts of the system, as well as the end-to-end outcome verification. This work aspires to enhance robustness and reliability of applications employing artificial intelligence, which are playing increasingly noticeable role in highly consequential decision-making processes across many industries and problem domains. INNs are invertible by construction and tractably trained simultaneously in both directions. This feature has untapped potential to improve the explainability of machine learning pipelines in support of their trustworthiness and is a topic of our current studies.

Keywords

Invertible, Autoencoder, Anomaly, Trustworthiness

1.  Introduction

This concept paper is inspired by a rapidly increasing role of machine learning in the decision- making process across a wide spectrum of domains, which brings to the forefront the importance of detecting anomalies and verifying the integrity of end-to-end inference flow, so the outcome of the system can be trusted. We propose that the general solution architecture paradigm for any mission critical decision support system, which leverages machine learning components, incorporates a layer of integrity verification around a running model to ensure trustworthiness of the pipeline. Our technique is applicable to machine learning inference flows significant enough to be protected by an extra security layer.

We build upon the concept of a Trusted Neural Network (TNN) [1], which leverages the revolutionary approach to achieve reversibility in neural networks introduced by Dinh [2] and subsequently incorporated into the Invertible Neural Network (INN) architecture by Ardizone [3]. An INN, which is invertible by construction, offers a remarkable data reconstruction capability that can be leveraged to validate that the inference flow pipeline is intact and that the output of it can be trusted. The result of that assessment in the form of the Inference Integrity

Score can be reported in real time and acted upon to safeguard system integrity by suppressing suspicious outcomes. The implementation of our inference verification paradigm employs the TNN-based test nodes comprising an AI-firewall layer offers a pragmatic approach to protecting machine learning pipelines and does not require any intricate intervention into the models themselves to handle adversarial inputs.

The remainder of this paper is organized as follows: Section 3 briefly reviews related work pertaining to safeguarding machine learning inference pipelines. It then elaborates on anomaly detection techniques [8] and Invertible Neural Networks touching upon normalizing flows [2] – the theory underlying the reversibility of deep neural networks. We also introduce the Framework for Easily Invertible Architectures (FrEIA) previously established by Ardizone [3], which provides an SDK to construct custom INN configurations to make it quick and approachable. We then discuss the remarkable ability of an Invertible Neural Network to reconstruct data from its compressed latent representation, outperforming traditional autoencoder architecture. In Section 4 we look at the Trusted Neural Network API and learn how a TNN node can be incorporated into a verification-based inference protection layer. Section 5 summarizes the study and offers our conclusion.

2.  Dependencies and Limitation

The anomaly detection solution presented in this work is based on the revolutionary Invertible Neural Network architecture, which was first introduced by Dinh [2] in 2016. The experiments leverage a concrete INN implementation described in [3] wrapped by the Framework for Easily Invertible Architectures, which offers an API mechanism to stack the infused with bijective functions invertible network nodes to achieve reversible deep learning.

3.  Related Works

3.1.   Machine Learning System Robustness

Machine learning system robustness, defined as building the reliable, secure, and fault-tolerant machine learning systems, is an active area of research. Much attention is given to strengthen adversarial resilience of the deep learning models themselves, but a verification-driven approach to validate the inference pipeline every step of the way provides an effective scheme to improve system robustness, while narrowing the gap between machine learning research and practice. As described by Apruzzese in “Real Attackers Don’t Compute Gradients” [4], every risk related to the inference pipeline’s loss of integrity can be effectively mitigated with a verification layer suitable for a given use case.

3.2.   Trusted Neural Network

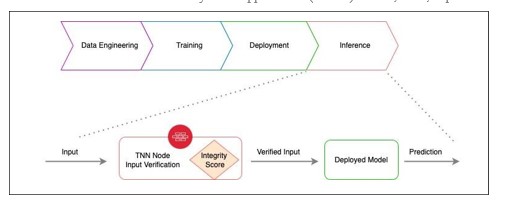
The diagram in Fig. 1 below depicts a conceptual template of a system comprising a Trusted Neural Network conceptualized in [1], where the output, in addition to the predicted result, includes an Inference Integrity Score to help assess trustworthiness of the outcome. It leverages the capability of an Invertible Neural Network deal with inverse problems and to reconstruct an input from an output, in their respective domains.

Figure 1. TNN Context Diagram [1]

A TNN is a general solution architecture paradigm and the concrete implementations reflecting the needs of specific problem domains can be derived from there.

Current methodologies employed to verify the integrity of Artificial Neural Networks leverage sampling strategies, which operate in the outer perimeter of the network. The TNN concept, however, incorporates the integrity measure as an integral part of the system. We propose that the inference flow is augmented with the inverse output-to-input verification steps, and that the INN-based Trusted Neural Network stackable nodes assume this responsibility – trained on the respective datasets, they are tasked with detecting and suppressing suspicious out-of-distribution data anomalies along the pipeline.

3.3.   Anomaly Detection

Anomaly detection is a process of identifying data that does not fit into a pattern of what is expected. As described in [5] and depicted in Figure 2, abnormal patterns in the phenomena characterized by low dimensionality can be easily discovered with an algorithmic approach based on acceptable value ranges, with simple clustering techniques, or even assessed visually. Giannoni [5] and subsequently Yin [6] put anomaly detection methods in several categories, such as statistical-based methods, probability-based methods, similarity-based methods, and most recently prediction-based methods.

Figure 2. Anomalies visualized [5]

The high dimensional scenarios surrounding systems with machine learning components highly dependent on integrity of the data, however, require more sophisticated multivariate statistics methods based on probability distributions and deep learning techniques. They are exemplified by generative neural networks, such as several classes of autoencoders, including novel INN- based autoencoders described [8] based on Invertible Neural Networks trained for anomaly detection.

3.4.   Autoencoders

Autoencoders belong to the family of unsupervised deep learning neural network models well suited for dimensionality reduction and have been described extensively in numerous works, such as [5] and [6], then referenced in [7]. The general idea around this type of neural network is to extract the most relevant features from input data and then learn how to reconstruct the original data from its compressed representation. For unexpected inputs, which the model has not seen during training, the reconstruction error should be higher, and crossing a configurable threshold, dependent on a problem domain, constitutes an anomaly.

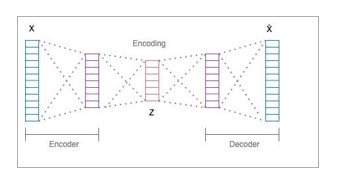
Figure 3. Classic Autoencoder [7]

As described in [7] and shown in Fig. 3, a classic autoencoder consists of an encoder and a decoder, implemented as fully connected neural networks. The encoder compresses the network input x into a lower dimensional latent representation z defined by the bottleneck. The decoder takes the output of the encoder and decodes the latent representation back to the original input x̂ . The information preserved in hidden neurons is considered as the encoded features. The learning process is based on minimizing the reconstruction error, which is assessed by comparing the reconstructed input with the original one. The learned representation corresponds to the final hidden state of the encoder network and acts as a summary of the input sequence.

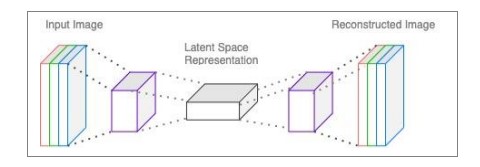
There are several variations of autoencoder architecture [7], such as a convolutional autoencoder, depicted in Fig. 4, which uses convolutional layers to create a compressed representations [6], or an LSTM autoencoder, proposed by Sutskever [9] and shown in Fig. 5, proficient in anomaly detection for sequential or time series data

Figure 4.Convolutional Autoencoder [7]

Figure 5.LSTM Autoencoder [7]

Yet another interesting extension of the autoencoder architecture is a variational autoencoder depicted in Fig. 6. It is capable not only of reconstructing the original input, but also enhancing it by generating new content based on the sampling from the learned probability density distribution of the input domain

Figure 6.Variational Autoencoder [7]

A compress-reconstruct type of challenge reflected in the autoencoder encoder-decoder architecture belongs to the class of “ill-posed” inverse problems, which are characterized by inherent ambiguity due to the existence of an information bottleneck. Such problems have been successfully addressed by the reversible neural network architecture applied in Invertible Neural Networks, which makes them an interesting option to help with our integrity verification undertaking. In this work we leverage previous findings and principles regarding several types of autoencoders together with reversible neural networks and apply the INN-based architecture for anomaly detection as a core of the TNN network integrity verification nodes.

3.5.   Invertible Neural Networks

As explored in [7] and referenced here for context, an Invertible Neural Network is a class of networks suited to solve ambiguity that characterizes inverse problems, where multiple parameter sets can produce the same observed outcome, as depicted in Fig. 7.

Figure 7.Forward mapping of x → y (left) and Inverse ambiguity (right) [7]

To express this ambiguity, the posterior probability of the parameters’ distribution, given an outcome y, must be learned so the most appropriate set can be selected. Such a model can perform log-density estimation of data points, leading to efficient inference and precise reconstruction of the inputs from the hierarchical features extracted by the model. This extraordinary capability to reconstruct the inputs corresponding to the encoder-decoder functionality makes INN a natural candidate to help solve the problem of anomaly detection.

An INN is trained simultaneously in the forward and reverse directions, Fig. 8.

Figure 8.Invertible Neural Network Conceptual Diagram

The forward learning process uses additional latent output variables to capture information otherwise lost, making the learning of the inverse process explicit.

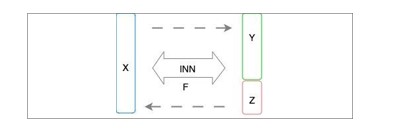
To solve the general inverse problem, we augment the observation space Y with a latent variable Z which follows a normal distribution and look for a bijective function F that can map Z back to X̂ .  An INN learns an invertible, stable, mapping between a data distribution PX and a latent

distribution PZ, typically Gaussian, as shown in Fig. 9.

Figure 9.. Reconstructing phenomenon X from observation Y

Invertibility of neural networks was spearheaded by Dinh [2] as “real-valued non volume preserving transformations” (Real NVP) architecture, who introduced a stack of invertible affine coupling blocks (Fig. 10), arranged in hidden layers.

Figure 10.Real NVP Affine Coupling Block [2]

Given a D-dimensional input x and d < D, the output y of an affine coupling layer follows the following equations [2]:

where s and t are functions from R^d product. R^D-d, and ⊙ is the Hadamard product or element-wise

Each block splits its input and output into two parts and applies transformations s (scale) and t (translation), which themselves do not have to be invertible – they can be quite complex and are often implemented as artificial neural networks, such as CNNs. It has been proven [3] that a stack of such invertible blocks makes the end-to-end layout also invertible. Based on this architecture, the Invertible Neural Network guarantees reversibility by its construction and solves the ambiguous inverse relationships directly.

3.6.   INN Trained as Autoencoder

As demonstrated by Nguyen [8] on MNIST, CIFAR and CelebA, and recently by Schwab [7], an INN has superb capability for anomaly detection on any type of data. We compared an INN- based implementation to conventional autoencoders for different bottleneck sizes, which demonstrated that INN autoencoders can achieve similar or better reconstruction results. It showed that the architecture restrictions on INN autoencoders to ensure invertibility do not negatively affect their performance, while the advantages of INNs are still preserved. This entails a tractable Jacobian for both forward and inverse mapping as well as explicit computation of posterior probabilities. It also provided an explanation for the saturation in reconstruction loss for large bottleneck sizes in classical autoencoders and concluded that an INN might not have any intrinsic information loss and thereby are not constrained by a maximal depth after which only suboptimal results can be achieved.

The concept of an INN entails bijective input-output mapping, so the dimensions of input x and output y augmented with z must be equal. As depicted in Fig. 11 below, an artificial bottleneck must be constructed to achieve autoencoder-like behaviour. It is accomplished by zeroing the latent z to make sure that no extra information is retained by the network in the inverse process of representation learning.

Figure 11.INN as Autoencoder [7]

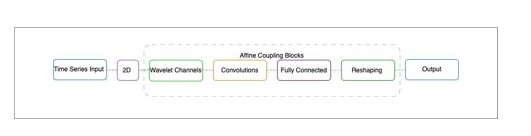
To easily create a fully invertible neural network, the solution leveraged FrEIA [3] to build a stack of invertible affine coupling blocks, depicted in Fig. 12.

Figure 12. INN Autoencoder Sample Network Layout [7]

A sample configuration in [7] consisted of three affine coupling layers leveraging convolutional transformations, followed by a fully connected coupling node. A multiplexing Haar wavelets transformation layer was applied to split each channel into 4 channels, with half the width and half the height. The experiments studied various approaches [10][11][12][13][14] and were conducted on two different time series datasets: an ECG diagnostics dataset [15] and the predictive maintenance (PdM) Airbus helicopter accelerometer dataset [16].

The reconstruction loss, indicative of healthy or abnormal samples, depicted in Fig.13 demonstrated the visible difference in the ability of the network to reconstruct the inputs it was trained on versus the data it has not seen.

Figure 13. INN Autoencoder Sample Network Layout [7]

The reconstruction loss on the anomalous samples was an order of magnitude greater as compared to the reconstruction error on the healthy validation data. The INN-autoencoder architecture also shows excellent performance [7], which renders it as an effective tool for inference integrity verification task

4.  Proposed Scheme for Inference Verification

 

4.1.   Solution Architecture

We propose a novel type of test-driven approach to ensure ML integrity, depicted in Fig. 14, which leverages the TNN nodes to protect against adversarial data at any given step of the inference pipeline, and thus guarding its integrity.

Figure 14.TNN Architecture [1]

The solution employs one or more Trusted Neural Network node(s) with INN at its heart configured for data reconstruction, so that the inputs of the modules comprising a pipeline can be subjected to a test, as indicated in Fig. 15 steps 1-6. Input and outputs of a module may or may not be in the data domain, which is the strength of Invertible Neural Networks, as compared to the classic autoencoder architecture.

A TNN [1] used as the module integrity verification node is composed of several high-level building blocks, each of which is independently defined, can be independently improved, and empirically tuned to fit the needs of any individual application use case.

Figure 15. TNN Architecture [1]

The integrity measure is computed by comparing an original input sample with the sample reconstructed by the Invertible Neural Network component embedded inside the TNN, and if too low, the overall prediction shall be discarded.

The similarity measure and the thresholds would vary per use case, and thus they must be designed specifically for any given domain.

The Trusted Neural Network [1] design pattern comes with REST API [17], depicted in Fig. 16, which in addition to the prediction outcome also returns the Inference Integrity Score.

Figure 16. TNN API Request and Response

4.2.   Output-Input Reconstruction

Several experiments were conducted to verify various INN configurations with respect to reconstructing the most probable input given an output. Described in [1], they followed the implementation examples provided in [3] using synthetic 2D coordinates points dataset, as well the MNIST dataset, which tested successfully as well (Fig. 17). It used batch size of 256, AdamW optimizer, and a variable learning rate adjusted halfway of the 100k iterations.

Figure 17. MNIST Experiment

The forward pass through the invertible network gives us a latent image Z, which fed to the network in the reversed flow outputs a regenerated X, noted as Xinverted.

The difference between the original input X entering the TNN and its counterpart Xinverted

regenerated by the network in the reverse flow is negligible:

A result like that which would be reflected in a high value of Inference Integrity Score and provide a successful test for a TNN node at a given step of the inference flow.

5.  Conclusion

This work proposes an easy to implement pragmatic scheme to enhance robustness of ML-driven systems through a test-driven inference flow verification layer based on the Trusted Neural Network nodes and their API abstraction. It leverages the Invertible Neural Network architecture and an open-source framework to construct the INN-based state-of-the-art anomaly detector. The paradigm is generalizable across problem domains and aspires to become a useful practice in drafting robust high level solution architectures for systems which incorporate machine learning capabilities and can benefit from additional measures of trustworthiness.

INNs are invertible by construction and tractably trained simultaneously in both, forward and reverse, directions. This feature has untapped potential to improve explainability of machine learning pipelines in support of their trustworthiness and is a topic of our current studies.

REFERENCES

[1] Schwab, M., Biswas, A., “Trusted Neural Network: Reversibility in Neural Networks for Network Integrity Verification”, World Academy of Science, Engineering and Technology International Journal of Computer and Systems Engineering Vol:16, No:04, 2022
[2] Dinh, L., Sohl-Dickstein, J. & Bengio, S., “Density estimation using Real NVP.” (2016)
[3] Ardizzone, L., Kruse, J., Wirkert, S.J., Rahner, D., Pellegrini, E., Klessen, R.S., Maier-Hein, L., Rother, C., & Köthe, U., “Analyzing Inverse Problems with Invertible Neural Networks.”, ArXiv, abs/1808.04730.
[4] Apruzzese, G., Anderson, H., Dambra S., Freeman D., Pierazzi F., Roundy K., “Real Attackers Don’t Compute Gradients: Bridging the Gap Between Adversarial ML Research and Practice”
[5] Giannoni, F., Mancini, M., Marinelli F., “Anomaly detection models for IoT time series data.”, 2018. [Online]. Available: arXiv:1812.00890.
[6] Yin, C., Zhang, S., Wang, J., Xiong, N., “Anomaly Detection Based on Convolutional Recurrent Autoencoder for IoT Time Series.”, In: IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 52, no. 1, pp. 112-122, Jan. 2022, doi: 10.1109/TSMC.2020.2968516.
[7] Schwab, M., Biswas, A., “Invertible Neural Networks for Time Series Anomaly Detection.”,
International Conference on Artificial Intelligence and Soft Computing AISC 2023
[8] Nguyen, TG.L., Ardizzone, L., Köthe, U., “Training Invertible Neural Networks as Autoencoders.”, In: Fink, G., Frintrop, S., Jiang, X. (eds) Pattern Recognition. DAGM GCPR 2019. Lecture Notes in Computer Science(), vol 11824. Springer, Cham. https://doi.org/10.1007/978-3-030-33676-9_31
[9] Sutskever, I., Vinyals, O., Le, O., “Sequence to sequence learning with neural networks.”, In: Proc. Adv. Neural Inf. Process. Syst., Montreal, QC, Canada, 2014, pp. 3104–3112.
[10] Kamat, P., Sugandhi, R., “Anomaly Detection for Predictive Maintenance in Industry 4.0- A survey.”, E3S Web Conf. 170 02007 (2020), DOI: 10.1051/e3sconf/202017002007
[11] Wen, L., Gao, L., Li, X., “A new deep transfer learning based on sparse auto-encoder for fault diagnosis.”, In: IEEE Trans. Syst., Man, Cybern., Syst., vol. 49, no. 1, pp. 136–144, Jan. 2019.
[12] Kingma D., Welling M., “Auto-Encoding Variational Bayes.”, In: arXiv:1312.6114
[13] Pintelas E., Livieris I.E., Barotsis N., Panayiotakis G., Pintelas P., “An Autoencoder Convolutional Neural Network Framework for Sarcopenia Detection Based on Multi-frame Ultrasound Image Slices.”, In: Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations; Crete, Greece. 25–27 June 2021; pp. 209–219.
[14] Yong, B., Brintrup, A., “Do Autoencoders Need a Bottleneck for Anomaly Detection?”, In: IEEE Access, vol. 10, pp. 78455-78471, 2022, doi: 10.1109/ACCESS.2022.3192134.
[15] ECG Dataset, http://www.timeseriesclassification.com/description.php?Dataset=ECG5000
[16] Predictive Maintenance Dataset, https://www.research- collection.ethz.ch/handle/20.500.11850/415151
[17] Fielding, R.: https://www.ics.uci.edu/~fielding/pubs/dissertation/fielding_dissertation.pdf

Authors

Malgorzata Schwab is an Enterprise Architect and IT executive leading digital transformation focused on innovative business strategies through cloud migrations and AI-augmented technologies. She is a PhD candidate at the Department of Computer Science and Engineering at the University of Colorado in Denver